绝对值不等式的解题技巧介绍：使用分类、换元、数形结合的方法

在不等式应用中,经常涉及重量、面积、体积等,也涉及某些数学对象(如实数、向量)的大小或绝对值.它们都是通过非负数来度量的.掌握解绝对值不等式的基本思路,会用分类、换元、数形结合的方法解不等式.解绝对值不等式的基本思想:去绝对值,常采用的方法是讨论符号和平方.

方法简述

1.分类讨论法

在解决某些数学问题的过程中,由于条件的不足,很难将问题整体性地转化为另一个熟悉的问题去解决,通过分类讨论,“化整为零,各个击破”来解决问题.

掌握分类讨论这一方法的关键是确定分类标准,进行分门别类的、既不重复又不遗漏的分析讨论.分类讨论法也是高考考查的重点思想方法.

通常引起分类讨论的原因,大致可归纳为如下几点:

(1)涉及的数学概念是分类定义的;

(2)涉及运算的数学定义、公式或运算性质、法则是分类给出的;

(3)涉及题中所给的限制条件或研究对象的性质而引起的;

(4)涉及数学问题中参变量的不同取值导致不同结果而引起的;

(5)涉及的几何图形的形状、位置的变化而引起的;

(6)一些较复杂或非常规的数学问题,需要采用分类讨论的解题策略解决的.

分类讨论的步骤:

(1)确定讨论的对象及其范围;

(2)确定分类讨论的标准,正确进行分类;

(3)逐类讨论,分级进行;

(4)归纳整合,作出结论.

例1 (1)不等式|x-1|-|x-5|<2的解集是(　).

A.(-∞,4)　B.(-∞,1)　C.(1,4)　D.(1,5)

(2)若关于x的不等式|ax-2|<3的解集为,则a=________.

点拨 切入点:“脱掉”绝对值符号;关键点:利用绝对值的性质进行分类讨论.

解答 (1)当x<1时,原不等式可化为-(x-1)+x-5<2,即-4<2,显然成立,所以此时不等式的解集为(-∞,1);

当1≤x≤5时,原不等式可化为x-1+x-5<2,即2x-6<2,解得x<4,又1≤x≤5,所以此时不等式的解集为[1,4);

当x>5时,原不等式可化为x-1-(x-5)<2,即4<2,显然不成立,所以此时不等式无解.

综上所述,原不等式的解集为(-∞,4).故选A.

(2)∵|ax-2|<3,∴-1<ax<5.

当a>0时,,与已知条件不符;

当a=0时,x∈R,与已知条件不符;

当a<0时,,且不等式的解集为,故a=-3.

反思 分类讨论是解绝对值不等式的常用方法,除了通过分类讨论去绝对值,还可以解决一些含参问题,但要注意讨论的完整性.

2.零点分段法

用零点分段法解绝对值不等式的步骤:(1)求零点;(2)划区间、去绝对值号;(3)分别解去掉绝对值的不等式;(4)取每个结果的并集,注意在分段时不要遗漏区间的端点值.

例2 已知函数f(x)=|x+a|+|x-2|.

(1)当a=-3时,求不等式f(x)≥3的解集;

(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.

点拨 含多个绝对值的问题,常利用零点分段法来去绝对值,转化为分段函数来求解.

解答 (1)当a=-3时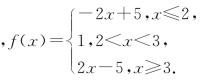

当x≤2时,由f(x)≥3得-2x+5≥3,解得x≤1;

当2<x<3时,f(x)≥3无解;

当x≥3时,由f(x)≥3得2x-5≥3,解得x≥4;

所以f(x)≥3的解集为{x|x≤1或x≥4}.

(2)由f(x)≤|x-4|得|x-4|-|x-2|≥|x+a|.

当x∈[1,2]时,则4-x-(2-x)≥|x+a|,

所以-2-a≤x≤2-a.

由条件得-2-a≤1且2-a≥2,即-3≤a≤0.

故满足条件的a的取值范围为[-3,0].

反思 注意在分段时不要遗漏区间的端点值,这是去绝对值时的常见错误.

3.利用绝对值的几何意义或图象解不等式

对于形如|x-a|+|x-b|>c或|x-a|+|x-b|<c的不等式,利用绝对值的几何意义或者画出左、右两边函数的图象去解不等式,更为直观、简捷,它体现了数形结合思想方法的优越性.

|x-a|+|x-b|的几何意义是数轴上表示x的点与点a和点b的距离之和,应注意x的系数为1.

例3 (1)若不等式对任意实数x恒成立,则实数a的取值范围是_________.

(2)不等式|x+1|-|x-2|>k的解集为R,则实数k的取值范围是_________.

点拨 切入点:绝对值的几何意义;关键点:把恒成立问题转化为最值问题.

解答 (1)∵|x-1|+|x+2|≥|(x-1)-(x+2)|=3,

∴,解得

即实数a的取值范围是

(2)解法一:根据绝对值的几何意义,设数x,-1,2在数轴上对应的点分别为P、A、B,则原不等式等价于PA-PB>k恒成立.因为AB=3,即|x+1|-|x-2|≥-3.故当k<-3时,原不等式恒成立.

例3答图

解法二:令y=|x+1|-|x-2|,

则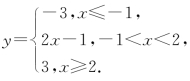作出图象如图所示.

要使|x+1|-|x-2|>k恒成立,从图象中可以看出,只要k<-3即可.故k<-3满足题意.

反思 掌握含有绝对值的函数图象画法,可以简化解绝对值问题的讨论过程,使解答更简单直观;当然也可以借助绝对值的几何意义解决这类问题.

例4 已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.

(1)当a=-2时,求不等式f(x)<g(x)的解集;

(2)设a>-1,且当时,f(x)≤g(x),求a的取值范围.

点拨 将不等式转化为f(x)-g(x)<0,通过作出函数图象来解不等式.

例4答图

(1)当a=-2时,

令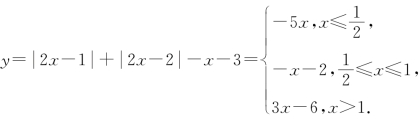

作出函数图象,如图所示,可知当x∈(0,2)时,y<0.

故原不等式的解集为

(2)依题意,原不等式化为1+a≤x+3,

故x≥a-2对都成立.

所以,即.所以a的取值范围是

反思 本题需要作出函数y=f(x)-g(x)的图象,由于函数本身带有两个绝对值,所以先使用零点分段法将其转化为分段函数形式,再画出图象取x轴下方的部分.

例5 已知函数

(1)求f(x)≥f(4)的解集;

(2)设函数g(x)=k(x-3),k∈R,若f(x)>g(x)对任意的x∈R都成立,求实数k的取值范围.

点拨 观察函数f(x),将其转化为的绝对值问题求解.

解答 (1)∵f(x)=+|x+4|,

∴f(x)≥f(4),即|x-3|+|x+4|≥9.

∴

解不等式①:x≤-5;解不等式②:无解;解不等式③:x≥4.

所以f(x)≥f(4)的解集为{x|x≤-5或x≥4}.(www.xing528.com)

例5答图

(2)由f(x)>g(x)得f(x)=|x-3|+|x+4|的图象恒在g(x)=k(x-3)图象的上方.

而g(x)=k(x-3)图象为恒过定点P(3,0),且斜率k变化的一条直线,

作出y=g(x)图象,如图所示.

其中kPB=2,A(-4,7),所以kPA=-1.

由图可知,要使得f(x)的图象恒在g(x)图象的上方,实数k的取值范围应该为-1<k≤2.

反思 本题(1)中通过分类讨论去绝对值来求解不等式;(2)中则通过数形结合来解决问题,这两种方法都是高中数学中非常重要的思想方法.

4.参变分离法

解含参数的不等式存在性问题,只要求出存在满足条件的x即可;不等式的恒成立问题,可转化为最值问题,即f(x)<a恒成立⇔a>f(x)max,f(x)>a恒成立⇔a<f(x)min.

例6 设函数

(1)求不等式f(x)>2的解集;

(2)若恒成立,求实数t的取值范围.

点拨 (2)中的恒成立问题,可变形为的恒成立问题,进一步转化成f(x)的最值来求解.

解答 (1)由题意得

当时,原不等式化为-x-3>2,解得x<-5,所以x<-5;

当时,原不等式化为3x-1>2,解得x>1,所以1<x<2;

当x≥2时,原不等式化为x+3>2,解得x>-1,所以x≥2;

综上所述,原不等式的解集为

(2)由(1)得

若恒成立,

则只需

综上所述,t的取值范围为

反思 对于含参数的恒成立问题、存在性问题等,常采用参变分离的方法将问题转化为最值问题来求解.

5.放缩法

放缩法是指要证明不等式A<B成立,有时可以将它的一边放大或缩小,寻找一个中间量,如将A放大成C,即A<C,后证C<B,这种证法便是放缩法.

例7 已知实数x、y满足:

点拨 观察已知条件和所证式子,发现可通过绝对值的三角不等式构造,然后适当放缩就可得证.

证明 ∵

又

∴

反思 本题用到了绝对值的三角不等式放缩来求最值,放缩法也是不等式证明中的一种常见方法.

易错解读

易错点1 转化过程不等价.

等价转化要求转化过程中前因后果是充分必要的,才能保证转化后的结果仍为原问题的结果.

例8 已知适合不等式|x2-4x+p|+|x-3|≤5的x的最大值为3,求p的值.

解答 错解:对此不等式无法进行等价转化,不理解“x的最大值为3”的含义.

正解:因为x的最大值为3,故x-3≤0,原不等式等价于|x2-4x+p|-(x-3)≤5,

即-x-2≤x2-4x+p≤x+2,则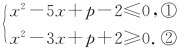

设①②的根分别为x1、x2(x2>x1)、x3、x4(x4>x3),则x2=3或x4=3.

若x2=3,则9-15+p-2=0,p=8;

若x4=3,则9-9+p+2=0,p=-2.

当p=-2时,原方程组无解,则p=8.

反思 实施等价转化时,我们要遵循熟悉化、简单化、直观化、标准化的原则,即把我们遇到的问题,通过转化变成我们比较熟悉的问题来处理;或者将较为烦琐、复杂的问题,变成比较简单的问题.但无论如何转化都要注意等价性,否则就会改变问题所求了.

易错点2 把存在性问题当成恒成立问题求解.

(1)对于恒成立问题或存在性问题常见基本类型:∀x∈D,f(x)>c,可以转化为f(x)min>c;∃x∈D,c>g(x),可以转化为c>g(x)min,∃x∈D,c=g(x),可以转化为c∈{y|y=g(x)}.对于由这些含有量词的命题组合而成的含有两个量词命题的问题,可以采取分步转化的方法来处理.

(2)对于含有参数的恒成立问题或存在性问题,常用的处理方法有分类讨论法或参数分离法,并借助于函数图象来解决问题.

例9 已知存在实数x使得不等式|x-3|-|x+2|≥|3a-1|成立,则实数a的取值范围是_________.

解答 由题意知这是一个存在性的问题,需求出不等式左边的最大值,令其大于等于|3a-1|,即可解出实数a的取值范围.

由题意借助数轴,得|x-3|-|x+2|∈[-5,5].

∵存在实数x使得不等式|x-3|-|x+2|≥|3a-1|成立,

∴5≥|3a-1|,解得-5≤3a-1≤5,即

反思 本题考查绝对值不等式,求解本题的关键是正确理解题意,区分存在问题与恒成立问题的区别.本题是一个存在问题,解决的是有的问题,故取|3a-1|≤5,即小于等于左边的最大值即满足题意.

经典训练

1.已知实数a、b满足ab<0,下列不等式成立的是(　).

A.　B.

C.　D.

2.若a>1,则不等式的解集是(　).

A.　B.

C.∅　D.R

3.若关于x的不等式的解集为∅,则实数a的取值范围为(　).

A.(-∞,1]　B.(-∞,1)　C.(-∞,5]　D.(-∞,5)

4.不等式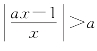的解集为M,且2∉M,则a的取值范围为(　).

A.　B.

C.　D.

5.若不等式对于一切实数x均成立,则实数a的最大值是(　).

A.7　B.9　C.5　D.11

6.对于实数x、y,若的最大值为(　).

A.5　B.4　C.8　D.7

7.已知f(x)=3x+1,若当时,有,则a、b满足的关系为________.

8.若x<5,n∈N*,则下列不等式:

③.其中能够成立的有_________.(填序号)

9.若关于x的不等式存在实数解,则实数a的取值范围是_________.

10.已知函数,若函数f(x)-g(x)≥m+1的解集为R,求m的取值范围.

11.已知函数

12.两个加油站A、B位于某城市东akm和bkm处(a<b),一卡车从该城市出发,由于某种原因,它需要往返A、B两个加油站,问它行驶在什么情况下到两个加油站的路程之和是一样的?

13.已知函数

(1)求证:-3≤f(x)≤3;

(2)求不等式f(x)≥x2-8x+15的解集.

14.已知实数a、b满足:关于x的不等式对一切x∈R均成立.

(1)请验证a=-2,b=-8满足题意;

(2)求出所有满足题意的实数a、b,并说明理由;

(3)若对一切x>2,均有不等式x2+ax+b≥(m+2)x-m-15成立,求实数m的取值范围.