理解不等式：基本数学关系在自然界和日常生活中的应用

不等关系是自然界中存在着的基本数学关系.《列子·汤问》中脍炙人口的“两小儿辩日”:“远者小而近者大”“近者热而远者凉”,就从侧面表明了现实世界中不等关系的广泛存在.日常生活中息息相关的问题,如“自来水管的直截面为什么做成圆的,而不做成方的呢?”“电灯挂在写字台上方怎样的高度最亮?”“用一块正方形白铁皮,在它的四个角各剪去一个小正方形,制成一个无盖的盒子,要使制成的盒子的容积最大,应当剪去多大的小正方形?”等,这些都属于不等关系的问题,需要借助不等式的相关知识才能得到解决.而且,不等式在数学研究中也起着相当重要的作用.

方法简述

1.性质法

不等式的基本性质:

(1)如果a>b,那么b<a;如果b<a,那么a>b.(对称性)

(2)如果a>b,且b>c,那么a>c,即a>b,b>c⇒a>c.

(3)如果a>b,那么a+c>b+c,即a>b⇒a+c>b+c.

推论:如果a>b,且c>d,那么a+c>b+d.即a>b,c>d⇒a+c>b+d.

(4)如果a>b,且c>0,那么ac>bc;如果a>b,且c<0,那么ac<bc.

(5)如果a>b>0,那么an>bn(n∈N,且n>1).

(6)如果a>b>0,那么

例1 若a>b>0,c<d<0,e<0,求证

点拨 根据不等号的方向和不等式的基本性质,可以得到两个分母之间的大小关系.

证明 ∵c<d<0,-c>-d>0,又a>b>0,

∴a-c>b-d>0,故.而

反思 本题考查学生对不等式性质的掌握及灵活应用.注意性质的使用条件.

2.比较法

比较法是最基本的方法,常用于不等式证明,具体可分为作“差”和作“商”两种方法.(1)作差法:a≥b⇔a-b≥0;(2)作商法其步骤是作差(商)—变形—判断符号.

例2 已知a、b、c均为正数,求证

点拨 比较两个式子的大小,常用比较法,本题适合用作差法解决.

证明 ∵a、b均为正数,

∴

同理,

三式相加,可得

∴当且仅当a=b=c时,等号成立.

反思 比较两个数(式子)的大小,一般用作差法,其步骤是:作差—变形—判断差的符号—结论,其中“变形”是关键,常用的方法是分解因式、配方等.

3.基本不等式

定理1:如果a、b∈R,那么a2+b2≥2ab(当且仅当a=b时取等号).

定理2:如果a、b∈R+,那么(当且仅当a=b时取等号).

在运用基本不等式解题时,一定要注意其成立的条件“一正,二定,三相等”,即“正数是前提,定值是基础,相等是保证”,三者缺一不可.

定理3:如果a、b、c∈R+,那么(当且仅当a=b=c时取等号).

算术—几何平均不等式:

(1)如果a1,a2,…,an∈R+,n>1且n∈N*,则叫作这n个正数的算术平均数叫作这n个正数的几何平均数;

(2)基本不等式

例3 已知x>0,y>0,且,求x+y的最小值.

点拨 要求x+y的最小值,根据极值定理,应构建某个积为定值,这需要对条件进行必要的变形,下面给出三种解法,请仔细体会.

解答 解法一:利用“1的代换”.

当且仅当,即y=3x时,取等号.

又,∴x=4,y=12.∴当x=4,y=12时,x+y取得最小值16.

解法二:由

∵x>0,y>0,∴y>9.

∴

∵y>9,∴y-9>0.∴

当且仅当,即y=12时,取得等号,此时x=4.

∴当x=4,y=12时,x+y取得最小值16.

解法三:由,得y+9x=xy.

∴(x-1)(y-9)=9.∴x+y=10+(x-1)+(y-9)≥10+2(x-1)(y-9)=16,

当且仅当x-1=y-9时,取得等号.

又,∴当x=4,y=12时,x+y取得最小值16.

反思 本题给出了三种解法,都用到了基本不等式,且都对式子进行了变形,配凑出基本不等式满足的条件,这是经常需要使用的方法,要学会观察,学会变形.另外,解法二通过消元,化二元问题为一元问题,要注意被代换的变量的范围对另外一个变量的范围的影响.

例4 已知a、b、c∈R+,且a+b+c=1,求证

点拨 根据已知条件,考虑作“1”的代换.

当且仅当时,取得等号.

反思 利用基本不等式解决问题时,常用到“1”的代换,本题实际是从要证明式子的结构特点进行整体巧用“1”代换,并运用均值不等式达到证明目的.

例5 已知a,b∈R+,a+b=1,求证

点拨 由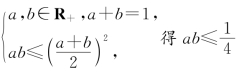,说明a、b∈R+,a+b=1的背后隐含

着一个不等式(www.xing528.com)

证明 ∵a,b∈R+,a+b=1,∴

而

∴

反思 本题利用基本不等式,求出,然后将整个式子都整理成和相关的形式,这样就能避免使用多次基本不等式导致等号条件不成立等错误.

易错解读

易错点1 忽视基本不等式中等号成立的条件.

使用均值不等式求解要检验等号成立的条件.

例6 函数的最小值为________.

解答

反思 本题容易出现将原式化为的错误,因为此时等号不能成立.

例7 求函数的最大值,下列解法是否正确?为什么?

解法一:∵

∴

解法二:∵,即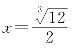时,等号成立,

∴

解答 以上两种解法均有错误.解法一错在取不到等号,即不存在x使得解法二错在不是定值(常数).

正解

当且仅当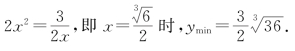

反思 均值不等式中,“一正、二定、三相等”三者缺一不可,所以在使用时需面面俱到,不能忽视任何一点.

易错点2 忽视题设条件或隐含条件.

重视题设中的已知条件及其隐含的范围限制,在满足条件的情况下解题.

例8 已知两正数x、y满足x+y=1,则的最小值为_________.

解答 错解一:因为对a>0,恒有,从而,所以z的最小值是4.

错解二:z=,所以z的最小值是

错解分析:错解一等号成立的条件是,即x=1且y=1,与x+y=1相矛盾.错解二等号成立的条件是,即相矛盾.

正解:令t=xy,则.由在区间上单调递减,有当时有最小值,所以当时,z有最小值

反思 此类问题要注意x、y本身的范围限制,不能盲目使用均值不等式解题,不然容易导致等号无法取到.

易错点3 转化过程不等价.

数学解题中经常用到转化的思想,在转化为简单问题时,注意满足充分必要性.

例9 已知-1<a+b<3且2<a-b<4,则2a+3b的取值范围是(　).

A.　B.　C.　D.

解答 错解:对条件“-1<a+b<3且2<a-b<4”不是等价转化,解出a、b的取值范围,再求2a+3b的取值范围,扩大了范围.

正解:用待定系数法,解出,求出结果为D.

反思 在多次应用不等式性质的时候,若等号不能同时成立时,会使所求范围扩大,因此在解有关不等式取值范围的题时,务必要检查等号能否成立.

经典训练

1.设a、b、c、d∈R,且a>b,c>d,则下列结论正确的是(　).

A.a+c>b+d　B.a-c>b-d　C.ac>bd　D.

2.设x、y∈R+且x+y=4,则3x+3y的最小值为(　).

A.10　B.6　C.4　D.18

3.设a、b∈R,若,则下列不等式正确的是(　).

A.b-a>0　B.a3+b3<0　C.a2-b2<0　D.a+b>0

4.若-1<α<β<1,则下列各式中恒成立的是(　).

A.-2<α-β<0　B.-2<α-β<-1

C.-1<α-β<0　D.-1<α-β<1

5.当时,函数y=x2(1-5x)的最大值为(　).

A.　B.　C.　D.无最大值

6.“a=1”是“对任意正数的(　).

A.充分不必要条件　B.必要不充分条件

C.充要条件　D.既不充分又不必要条件

7.若正数a、b满足ab=a+b+3,则ab的取值范围是________.

8.若记号“*”表示求两个实数a与b的算术平均的运算,即,则两边均含有运算“*”和“+”,且对任意3个实数a、b、c都能成立的一个等式可以是_________.

9.若a、b、c∈R,a>b,则下列不等式成立的是________(填上正确的序号).

①;②a2>b2;③;④.

10.已知且a≠b,比较与a+b的大小.

11.已知a、b、x、y都是正数,且a+b=1,求证:(ax+by)(bx+ay)≥xy.

12.已知a、b、x、y∈R+,x、y为变量,a、b为常数,且a+b=10,,x+y的最小值为18,求a、b.