基本不等式及其应用：完整指南

最常用的基本不等式:若a、b∈R,则a2+b2≥2ab,当且仅当a=b时等号成立;若a、b∈R+,则

方法简述当且仅当a=b时等号成立.

1.转化法

例1 设a>b>c,n∈N*,且恒成立,求n的取值范围.

点拨 将含有变量a、b、c的式子移到不等式左边,得到恒成立,于是本题就转化为运用基本不等式,去求不等式左边最小值的问题.

解答 ∵a>b>c,∴a-b>0,b-c>0,a-c>0.

由已知,得

则

∴.若恒成立,则n≤4.

反思 本题也可令x=a-b,y=b-c,故原不等式化为,所以,故有n≤4.

2.基本不等式法

例2 已知:a、b、c∈R,求证:a2+b2+c2≥ab+bc+ac.

点拨 本题的关键是对式子a2+b2+c2进行配、凑,将a2+b2+c2分成三组,并通过三次基本不等式的使用,对不等式进行证明.

证明 由a、b、c∈R,得

当且仅当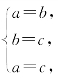即a=b=c时,等号成立.

反思 本题中使用了基本不等式法,要注意在所证明的不等式中,若要等号成立,必须使三次使用基本不等式的等号成立条件同时满足.本题也可通过作差法进行证明.

3.分类讨论法

分类讨论的思想方法,实质上是“化整为零,各个击破,再积零为整”的数学策略.对问题实行分类与整合,确定分类标准后等于增加了一个已知条件,实现了有效增设,将大问题(或综合性问题)分解为小问题(或基础性问题),优化解题思路,降低问题难度.

例3 设a、b∈R,a·b=1,求a+b的取值范围.

点拨 由a·b=1,得a≠0,则,代入,但是要用均值不等式时,要求对a>0或a<0,进行分类讨论才能解决此题.

解答 由a·b=1,得a≠0,故有

当a>0时,当且仅当,即a=1时,等号成立;

当a<0时,则,即a+b≤-2,当且仅当,即a=-1时,等号成立.

综上所述,a+b的范围为(-∞,-2]∪[2+∞).

反思 本题也可由a与同号,令,得,所以|y|≥2,解得y≥2或y≤-2,即得a+b的范围为(-∞-2]∪[2,+∞).

4.巧用“1”代换

高中数学中有不少题目,如果能巧妙地利用“1”的代换,将大大地简化计算量和计算过程,能收到事半功倍的良效.

例4 如果a、b∈R+,且a+b=1,求证:,并指出等号成立的条件.

点拨 如何巧用“1”建立起已知与未知的必然联系,是解本题关键所在,从要证的不等式左边出发构造“1”,可以在左边同乘以“1”,即同乘以a+b,也可以将a+b=1代入左边的分子,将“1”变为a+b,将“4”变为4(a+b).

证明 由于a+b=1,则,当且仅当且a+b=1,即时,等号成立.

反思 本题实际是从要证明式子的结构特点进行整体巧用“1”代换,并运用均值不等式达到证明目的,要注意的是,以下方法存在错误,不可使用:(www.xing528.com)

由于,又由a+b=1可得当且仅当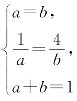时,则a、b不存在,即等号不成立.

易错解读

易错点1 等号成立的条件不一致而导致错误.

注意运用均值不等式求最值时的条件:“一正、二定、三相等”.

例5 已知x>0,y>0且2x+y=1,求的最小值.

某同学解法如下:因为x>0,y>0,则即

又由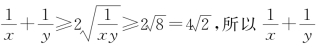的最小值为.该解法是否正确,为什么?

解答 这个解法是错误的.原因在于不等式,等号成立的条件是2x=y,而不等式等号成立的条件是x=y,故上述等号不能同时成立.本题正确解法可参考例4的方法来解,请同学们自己完成.

反思 在应用均值不等式解题时,特别是在多次运用时,注意检验等号成立的条件能否同时取到,若不能同时取得,则解答错误.

易错点2 取不到等号而导致错误.

注意检验等号成立的条件能否取到.

例6 设x≥5,求的最小值.

某同学解法如下:由x≥5,则

有的最小值为4.

当且仅当,即x=3时,等号成立.该解法是否正确,为什么?

解答 该解法是错误的.因为x≥5时,所以4不是的最小值.

正解:由x≥5,则,当且仅当,即x=3时,等号成立.因为x=3不在区间[5,+∞)内,令,则当x≥5时,y单调递增,所以y的最小值即的最小值为

反思 在应用均值不等式解题时,忽视了均值不等式中等号成立的条件:“一正、二定、三相等”中的第三个条件,所以解题时需检验等号成立的条件.

经典训练

1.是a>0,b>0的_________.

2.若x>1,则的最小值是________.

3.若x、y∈R+且x+4y=1,则xy的最大值是_________.

4.若a+b=2(a、b∈R),则3a+3b的最小值为________.

5.命题:若a>1>c且a+1+c=0,则判断此命题是真命题还是假命题,证明你的结论.

6.若a、b∈R+,且a≠b,求证:

7.求函数的最值.

8.用30m长的建筑材料沿墙砌成两居室,请你设计一方案,使围成的面积最大.

9.若a、b∈R+且a+b=ab-3,求ab的范围.

10.若x、y∈R+,且x+y=4,求使不等式恒成立的实数m的范围.