解决其他不等式的方法：3.3教程

本节主要研究分式及含有绝对值的不等式的问题,其解题思想方法简述如下.

方法简述

1.分类讨论法

例1 解关于x的不等式

点拨 按分式不等式的解法,转化为整式不等式得(x-2)[x-(3a+1)]>0,为区分与此不等式相应的二次函数图象的开口方向、相应的二次方程的两实根的大小关系,必须对字母a的取值情况进行讨论.

解答 原不等式转化为(x-2)[x-(3a+1)]>0.

当3a+1>2,即时,不等式的解集为(-∞,2)∪(3a+1,+∞);

当3a+1=2,即时,不等式的解集为{x|x≠2,x∈R};

当3a+1<2,即时,不等式的解集为(-∞,3a+1)∪(2,+∞).

反思 本题在比较一元二次方程(x-2)[x-(3a+1)]=0的两根x1=2与x2=3a+1的大小时,可采用作差比较法,即(3a+1)-2=3a-1为正、负、零,分别进行讨论.本题也可转化为不等式组来求解.

2.数形结合思想

例2 对一切实数x,若|x-5|+|x+4|>a恒成立,求实数a的取值范围.

点拨 要使已知不等式对一切实数x恒成立,只需实数a比式子|x-5|+|x+4|的最小值还小即可,可利用绝对值的几何意义来求解.

解答 由|x-5|+|x+4|的几何意义为:数轴上的动点P(x,0)到定点A(5,0),B(-4,0)两点的距离之和,当动点P在A、B两点之间时,|PA|+|PB|最短,且|PA|+|PB|=|AB|=9,即|PA|+|PB|=|x-5|+|x+4|≥9>a,故a<9.

反思 本题也可用绝对值定义去掉绝对值,并化简函数y=|x-5|+|x+4|=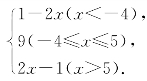画图象,易知a<9.

3.转化法

例3 关于x的不等式的解集为R,求实数m的取值范围.

点拨 由于已知分式不等式的分母,通过去分母,转化为一元二次不等式解集为R的情形来求解.

解答 由x2+x+1>0,

则3x2+2x+2<mx2+mx+m.

即(3-m)x2+(2-m)x+2-m<0的解集为R.

当m=3时,不等式-x-1<0,不满足题意;

当m≠3时,则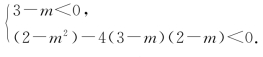解得

综上所述,m的取值范围为

反思 转化的关键是去分式不等式的分母,化分式不等式为整式不等式,所乘的多项式符号,是“正”,还是“负”,值得注意,否则就影响不等号方向.本题体现了由繁到简,由分式到整式,由不熟悉到熟悉的思维过程.

易错解读

易错点1 不等式的性质运用有误.

在运用不等式的基本性质解题时,要注意各个性质的使用条件,保证解题的正确性.(www.xing528.com)

例4 设集合,且A∪B=B,求实数a的取值范围.

某同学解法如下:因为|x-a|<2,所以a-2<x<a+2,即A={x|a-2<x<a+2}.

由,得2x-1<x+2,所以x<3,即B={x|x<3},

因为A∪B=B,则A⊆B,所以a+2≤3,故a≤1.以上解法是否正确,为什么?

解答 以上解法是错误的.由,得2x-1<x+2是错误的,因为x+2的正负不确定,不能去分母.

正解:由,解得-2<x<3,

即B={x|-2<x<3}.又A∪B=B,则A⊆B,所以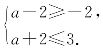解得0≤a≤1.

反思 分式不等式求解是不等式求解中很容易出错的题型,往往容易直接两边同乘去分母,主要是由于对不等式性质的条件没有很好掌握,要引起重视.

易错点2 思维不严密,考虑不全面.

例5 关于x的不等式的解集为{x|-1<x<3},求实数m的取值范围.

某同学解法如下:因为x2-2x-3<0的解集为{x|-1<x<3}与原不等式同解,所以mx2+2(m+1)x+9m+4<0在R上恒成立.当m=0时,2x+4<0在R上不恒成立;当m≠0时,解得.以上解法是否正确,为什么?

解答 以上解法不正确.在上述解法中,由与x2-2x-3<0同解,得出关于x的不等式mx2+2(m+1)x+9m+4<0在R上恒成立是错误的.

正解:由条件与x2-2x-3<0同解,当m≥0时,显然不符合条件.

所以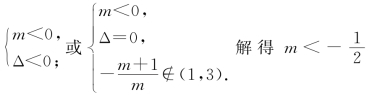或m∈∅.所以m的取值范围为

反思 本题错解是考虑不全的典型表现,如与x2-2x-3<0同解,但-x2+10x-25=-(x-5)2,当x=5时,-x2+10x-25<0在R上不恒成立.

经典训练

1.不等式的解集为_________.

2.当实数a=________,则关于x的不等式的解集为∅.

3.不等式的解集为________.

4.不等式(x+1)(1-|x|)>0的解集为________.

5.若不等式|x-2|≤k的解集为[-1,5],则k的值为(　).

A.2　B.3　C.4　D.5

6.解不等式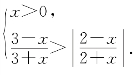

7.已知关于x的不等式的解集为,求a+b的值.

8.定义运算如下:,解不等式x*(x+1)>0.

9.解关于x的不等式

10.关于x的不等式对一切x∈R恒成立,求实数a的取值范围.