解答一元二次不等式的方法：一步步教学

本节研究只含有一个未知数,并且未知数的最高次数是二次的不等式的解法.一般地,先将一元二次不等式化成一般形式,再通过因式分解转化为两个一元一次不等式组,或者结合二次函数的图象的性质来求解.

方法简述

1.转化法

例1 若不等式2x-1>m(x2-1)对满足-2≤m≤2的所有m都成立,求实数x的取值范围.

点拨 本例从不等式的形式上看似乎是一个关于x的一元二次不等式的问题.仔细分析,实质上我们可以将问题转化为一个关于m的一元一次且解集为[-2,2]的不等式,借助图象很容易求出x的取值范围.

解答 原不等式化为(x2-1)m-(2x-1)<0.

设函数f(m)=(x2-1)m-(2x-1),且-2≤m≤2.

由题意,等价转化为

反思 利用等价转化法在解与不等式有关的问题时,我们通常是把所求的不等式转化为不等式组或一元二次不等式来求解,而本题则是将一元二次不等式巧妙地转化为关于m的一元一次不等式来求解,这样也充分体现了高维向低维转化、由难向易转化,起到了事半功倍之效.

例2 已知关于x的一元二次不等式ax2+bx+c<0的解集为求关于x的一元二次不等式ax2-bx+c>0的解集.

点拨 由已知的不等式解集可知a<0,且应是方程ax2+bx+c=0的两个根,这样可由根与系数的关系,求出再将所求的不等式ax2-bx+c>0,转化为x2易求其解.

解答 考虑二次函数y=ax2+bx+c的图象,可知ax2+bx+c<0的解集是的等价条件是a<0,且为方程ax2+bx+c=0的两根,由韦达定理,得.因为a<0,所以由不等式ax2-bx+c>0,得,即,解得,故所求的不等式的解集为.

反思 本题可进行更一般的推广:已知关于x的不等式ax2+bx+c>0(a≠0)的解集为(α,β),求关于x的一元二次不等式ax2+bx+c<0的解集.请同学们自己完成解答.

例3 不等式x2-3>ax-a对一切3≤x≤4恒成立,则符合要求的自然数a有_______个.

点拨 将不等式两边分别看作两个函数f(x)=x2-3与g(x)=a(x-1),这两个函数的图象和性质都是我们比较熟悉的,通过对上述函数图象的分析解决问题.

解答 结合函数f(x)=x2-3与g(x)=a(x-1)图象,

当3≤x≤4时,函数y=f(x)的图象在函数y=g(x)的图象上方.

因为f(3)=6,f(4)=13,所以.

所以,符合要求的自然数a有3个.

反思 本题将不等式的问题转化为函数的问题,并通过数形结合的思想对问题进行分析.

2.分类讨论法

例4 解关于x的不等式2x2+(1-2a)x-a<0.

点拨 解含参数的一元二次不等式也应与通常解法一样,首先求出相对应的一元二次方程2x2+(1-2a)x-a=0的根x1=a,x2=,在比较这两个根的大小时,确定分类讨论的标准.

解答 因为2x2+(1-2a)x-a<0,

相应一元二次方程的判别式Δ=(1-2a)2-4×2×(-a)=(2a+1)2≥0,

所以方程2x2+(1-2a)x-a=0的两根为.

当a>时;

当时

当时,解集为空集.

反思 在解含参数一元二次不等式时,对参数进行分类讨论的过程中,其分类标准是解决问题的关键,讨论的是根x1与x2大小,而根又可通过分解因式(2x+1)(x-a)=0求得x1=a,x2=.当时,根据两个根的大小不同,确定分类讨论的标准.

3.构造法

构造法在数学解题中的作用主要表现在以下两个方面:

(1)许多数学问题本身具有构造性的要求,或者说可以通过构造而直接求解.

(2)许多问题,如果通过构造相应的数学对象(如方程、函数、数列、图形、命题等)作为辅助工具,则问题容易解决.数学解题中运用构造法,常常体现为不对问题本身求解,而是构造一个与之相关的辅助命题.

例5 已知集合A={x|(1-x)(x-3)>0},关于x的不等式组的解集为B,且A⊆B,求实数a、b的取值范围.

点拨 由于集合B中的a与b是未知的,其不等式解集是很难求出的,为此,不妨尝试根据集合B中的一元二次不等式,构造出相应的二次函数f(x)=x2-2x+a与g(x)=x2-2bx+5.又由集合A=(1,3),且A⊆B,借助图象,易求其解.

解答 设函数 f(x)=x2-2x+a,g(x)=x2-2bx+5.

由A=(1,3)要使A⊆B,

则f(x)、g(x)的图象必须满足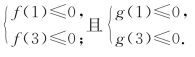

解得a≤-3且b≥3.(www.xing528.com)

反思 集合A的二次项系数为“负”值,乘“-1”转化为“正”值时,才能得到解集A=(1,3),这一点对初学者是易错之处.由于集合B不易求出,想到构造一元二次式所对应的二次函数,再借助二次函数的图象,使问题转化为解不等式组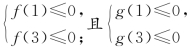来解.

4.数形结合思想

数形结合的思想,其实质是将抽象的数学语言与直观的图象结合起来,关键是代数问题与图形之间的相互转化,它可以使代数问题几何化,几何问题代数化.在运用数形结合思想分析和解决问题时,要注意三点:第一,要明白一些概念和运算的几何意义以及曲线的代数特征,对数学题目中的条件和结论既分析其几何意义又分析其代数意义;第二,恰当设参、合理用参,建立关系,由数思形,以形想数,做好数形转化;第三,正确确定参数的取值范围.

例6 关于x的不等式(k-5)x2-(5-k)x-k+10>0的解集为R,求实数k的取值范围.

点拨 由已知关于x的不等式解集为R,应当先分析最高次项系数为0的情况是否符合题意,因为此时该不等式不是二次不等式.之后再分析当最高次项系数不为零的时候,二次不等式对应的函数图象特征.

解答 当k=5时,不等式0·x2-0·x-5+10>0恒成立,解集为R,符合题意.

当k≠5时,不等式对应的二次函数y=(k-5)x2-(5-k)x-k+10图象应在x轴上方,

所以开口向上,且与x轴没有交点,则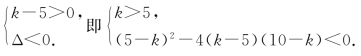解得5<k<9.

综上所述,5≤k<9.

反思 本题体现了“数”与“形”的有机结合,通过二次函数的图象特征反映不等关系.本题也可以变式为关于x的不等式(k-5)x2-(5-k)x-k+10≥0的解集为空集,求实数k的取值范围.

易错解读

易错点1 分类讨论不全而导致错误.

分类讨论中注意特殊情况的讨论,如二次项系数等于0等.

例7 关于x的不等式kx2-6kx+k+8≥0的解集为R,求实数k的取值范围.

某同学解法如下:由kx2-6kx+k+8≥0的解集为R,得Δ=36k2-4k(k+8)≤0,解得0≤k≤1.以上解法是否正确?说明理由.

解答 这个解法是错误的,没有讨论k=0情况,而且忽略了k>0这一必要条件.

正解:当k=0时,解集为R.当k≠0时,由解集为R,等价转化为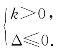解得k∈(0,1].综上所述,k∈[0,1].

反思 在运用分类讨论思想研究问题时,必须做到“不重、不漏”,而且要按照相同的标准进行讨论,只有掌握了分类讨论思想,在解题时才不会出现漏解的情况.

易错点2 变形不等价而导致错误.

将复杂问题或不熟悉的问题转化为简单问题的过程中要注意保持等价性.

例8 解不等式(x-1)(2-x)>0.

某同学解法如下:由方程(x-1)(2-x)=0,解得x1=1,x2=2.

所以原不等式解集为(-∞,1)∪(2,+∞).以上解法是否正确?说明理由.

解答 这个解法是错误的,错误的主要原因在于解一元二次不等式的过程中,把求相应方程的根,大于号的取两根之外,小于号的取两根之间,作为形式上套用,却忽视了二次项系数为正数的大前提.

正解:把原不等式转化为(x-1)(x-2)<0,解集为(1,2).

反思 例如,在求不等式2x(x+1)>3(x+1)的解集时,易产生两边约去x+1,从而得解集为,这种不等价的错误.等价转化要求转化过程中前因后果是充分必要的,才能保证转化后的结果仍为原问题的结果.

经典训练

1.不等式-x2+x<2的解集为________.

2.集合A={x|(2-x)(x+1)>0},B={x|(x-a)(x-b)>0},若a=-2是A∩B=∅的充分条件,则实数b的取值范围是________.

3.写出一个一元二次不等式_________,使它的解集为(-1,3).

4.集合P={0,b},Q={x|x2-3x<0,x∈Z},P∩Q≠∅,则b的值为(　).

A.1　B.2　C.1或2　D.8

5.解关于x的不等式(x-a)(x-2a)>0(a∈R).

6.已知不等式ax2+bx+3>0的解集为(-3,1),求a-b的值.

7.关于x的不等式(1-m2)x2+(m-1)x+1>0的解集为R,求实数m的取值范围.

8.△ABC中三边分别为a、b、c,求证:无论x取何值,总有b2x2+(b2+c2-a2)x+c2>0成立.

9.某厂家生产消费品每件120元,不加收附加税时,每年大约销售80万件,若征收附加税,每销售100元要征税r元(叫作税率r%),则每年的销售量将减少件,要使每年在此项经营中所收取的税金不少于256万元.r应怎样确定?

10.设不等式组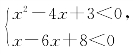的解集为M,关于x的不等式2x2-9x+m<0解集为N,若M∩N=M,求实数m的取值范围.