等差数列的基本概念、公式及其应用

一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,这个数列就叫等差数列,这个常数叫作等差数列的公差,通常用字母d表示.用递推公式表示为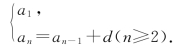通项公式为an=a1+(n-1)d.等差数列的前n项求和公式为Sn=

如果a、A、b成等差数列,那么A叫作a与b的等差中项,即a、A、b成等差数列⇔A

设数列{an}是等差数列,且公差为d,m、n、p、q∈N*,若m+n=p+q,则am+an=ap+aq.

方法简述

1.基本量法

在量制中,约定地被认为是相互独立的量称为基本量.在等差数列中,第一项a1和公差d是两个基本量.在解题过程中,利用a1和d表示已知条件,并利用方程思想进行求解,获得基本量a1和d,进而解决问题的方法称为基本量法.

例1 已知等差数列{an}满足a2=0,a6+a8=-10,求a2014.

点拨 根据等差数列的通项公式的概念,将已知条件中的两个等式表示为a1和d这两个基本量的方程,并求解方程.

解答 解法一:设等差数列{an}的公差为d.

由已知条件,得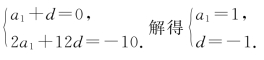

∴an=-n+2.∴a2014=-2012.

解法二:设等差数列{an}的公差为d.

由a6+a8=-10,可得2a7=-10,∴a7=-5.

∴.∴an=a2+(n-2)d=-n+2.

∴a2014=-2012.

反思 等差数列的两个基本量为a1和d,一旦基本量确定,在已知项数的情况下,整个数列中的每一项都可以相应确定.

例2 设S2为等差数列{an}的前n项和,若S3=3,S6=24,求a9.

点拨 根据等差数列的前n项和的概念和公式,将已知条件中的两个等式表示为a1和d这两个基本量的方程,并求解方程.

解答 由题意,得

∴∴a9=a1+8d=15.

反思 等差数列的两个基本量为a1和d,一旦基本量确定,在已知项数的情况下,整个数列中的每一项都可以相应确定.

2.定义法

所谓定义法,就是直接用数学定义解题.数学中的定理、公式、性质和法则等,都是由定义和公理推演出来的.定义是揭示概念内涵的逻辑方法,它通过指出概念所反映的事物的本质属性来明确概念.

定义是千百次实践后的必然结果,它科学地反映和揭示了客观世界的事物的本质特点.简单地说,定义是基本概念对数学实体的高度抽象.用定义法解题,是最直接的方法.

(1)求证:数列为等差数列;

(2)试问:数列中akak+1(k∈N*)是否仍是数列{an}中的项?如果是,请指出是数列的第几项;如果不是,请说明理由.

点拨 第(1)题中证明数列为等差数列,只需根据定义,证明为定值,所以要对已知的等式进行变形,构造出

第(2)题则可以利用数列{an}的通项公式的定义,来进行验证.

解答 (1)证明:由已知,得anan+1+2an=4anan+1+2an+1.

则2an-2an+1=3anan+1,所以

所以数列为首项,公差为的等差数列.

(2)由(1)可得数列的通项公式为,所以

当一定是正整数,所以是正整数.

所以akak+1是数列{an}中的项,是第项.

反思 明确等差数列的定义以及等差数列通项公式,并且进行合理运用,可以帮助我们解决此类问题.

例4 等差数列{an}、{bn}的前n项和分别为Sn、Tn,且为整数的正整数n的值.

点拨 根据等差数列前n项和的定义,可以得到1)·an.

解答

又.∴n-2=1,3,11,33.∴n=3,5,13,35.

反思 等差数列中,若m、n、p、q∈N*,则m+n=p+q⇒am+an=ap+aq,可以得到an与S2n-1的关系.

3.方程思想

方程的思想,是对于一个问题用方程解决的应用,也是对方程概念本质的认识,是分析数学问题中变量间的等量关系,构建方程或方程组,或利用方程的性质去分析、转换、解决问题.要善用方程和方程组观点来观察处理问题.方程思想是动中求静,研究运动中的等量关系.当一个问题可能与某个方程建立关联时,可以构造方程并对方程的性质进行研究以解决这个问题.

例5 在等差数列{an}中,a2+a3+a4=-12,a1a3a5=80,求通项an.

点拨 利用等差数列的性质,将两个等式转化为关于a1、a5的方程,并利用方程求解来解决问题.

反思 等差数列的基本量始终是a1和d,将这两个基本量作为未知数,构建方程进行求解是数列问题中经常使用的技巧.

4.利用已知结论法

在求解过程中,合理运用已知的条件和求解过程中产生的结论,分析所求的内容与已知结论之间的内在联系,可以使得求解的过程得到简化.

例6 已知数列{an}的前n项和为Sn=n2-12n,若Tn=|a1|+|a2|+|a3|+…+|an|,求Tn.

点拨 Tn是{|an|}的前n项和,而Sn是{an}前n项和,an的正负影响到了Tn与Sn的关系,所以必须先对an进行讨论.

解答 当n=1时,a1=S1=-11.

当n≥2时,

an=Sn-Sn-1=n2-12n-(n-1)2+12(n-1)=-12n+2n-1+12n-12=2n-13.

检验n=1时,a1=-11.∴an=2n-13.

当n≤6,n∈N*时,an<0;n≥7,n∈N*时,an>0.

∴当n≤6,n∈N*时,Tn=-(a1+a2+…+an)==-n2+12n.(www.xing528.com)

当n≥7,n∈N*时,

Tn=-(a1+a2+…+a6)+(a7+a8+…+an)=36+=n2-12n+72.

∴Tn=

反思 研究an的正负,并尝试用已知条件Sn来表示Tn是此类问题比较理想的求解方式.

5.知识迁移法

所谓知识迁移法就是利用新旧知识间的联系,启发学生进行新旧知识对照,由旧知识去思考、领会新知识,学会学习的方法.数学的各个组成部分不是孤立存在,而是互相联系,互为因果的.学生的思维过程就是揭示和建立新旧知识联系的过程.任何自主探索都必须有起点,有依托,不能切断知识之间的内在联系.通过引思、回顾、概括、归纳旧知,形成程序性知识,建立良好的知识网络结构,从而使自主探索成为可能.

例7 设数列{an}为等差数列,其前n项和为Sn,a1+a4+a7=99,a2+a5+a8=93,若对任意n∈N*,都有Sn≤Sk成立,求k的值.

点拨 由于等差数列的前n项和Sn可以看成定义域为正整数集或它的有限子集{1,2,…,n}的二次函数,所以只需求出Sn的表达式,再利用二次函数求最值的方法进行研究即可.

解答 对任意n∈N*,都有Sn≤Sk成立,则Sk是Sn的最大值.

由等差数列的性质,有a1+a7=2a4,a2+a8=2a5,

代入已知条件,得a4=33,a5=31.

所以d=a5-a4=-2,a1=33-3d=39.

解法一:

当n=20时,Sn有最大值,故k的值为20.

解法二:an=39-2(n-1)=41-2n.

由

∴当n=20时,Sn取得最大值,故k=n=20.

反思 本题除了从Sn出发研究问题,也可以利用Sn和an的关系来研究问题.

易错解读

易错点1 忽视常数列也是等差数列的事实.

判断必要性时要注意其中的特例.

例8 设{an}是等差数列,m、n、p、q∈N*,则m+n=p+q是am+an=ap+aq的(　).

A.充分不必要条件　B.必要不充分条件

C.充要条件　D.既不充分也不必要条件

解答 充分性成立:

当m+n=p+q时,am+an=2a1+(m+n-2)d=2a1+(p+q-2)d=ap+aq成立.

必要性不成立:

反例:当{an}为常数列时,例如an=1,则任取m、n、p、q∈N*,都有am+an=ap+aq.

综上所述,故选A.

反思 解题中需注意特殊情况,比如本题中常数列也是等差数列,同时非零的常数列也是等比数列.

易错点2 漏解.

分类讨论时要明确分类对象和分类标准.

例9 已知等差数列{an}的通项公式为an=2n-14(n∈N*),Sn是数列{an}的前n项和,则当n=_________时,Sn取最小值.

解答 令an≤0,即2n-14≤0,解得n≤7.

则当1≤n≤6时,an<0;当n=7时,an=0;当n≥8时,an>0.

所以n=6或7.

反思 解题时需注意考虑完整,讨论不重复不遗漏,才能确保求出所有的结果.

经典训练

1.在等差数列{an}中,a2=2,a3=4,则a10=________.

2.等差数列{an}的前n项和为Sn,若a2+a6+a7=18,则S9的值是________.

3.设等差数列{an}的前n项和为Sn,若1≤a5≤4,2≤a6≤3,则S6的取值范围是_________.

4.已知等差数列{an}的公差为d(d≠0),且a3+a6+a10+a13=32,若am=8,则m为(　).

A.12　B.8　C.6　D.4

5.已知方程(x2-2x+m)(x2-2x+n)=0的四个根组成一个首项为的等差数列,则|m-n|=(　).

A.1　B.　C.　D.

6.设数列{an}的前n项和为Sn,若,求证:数列{an}为等差数列.

7.已知在等差数列{an}中,a1=31,Sn是它的前n项和,S10=S22.

(1)求Sn;

(2)这个数列的前多少项的和最大?求出这个最大值.

8.已知等差数列{an}单调递减且满足:a2a10=-48,a5+a7=-8,{an}的前n项和为Sn.

(1)求|an|的表达式;

(2)求数列{|an|}的前n项和Tn.