转化法在解决数学问题的应用实例

方法简述

1.转化法

解决数学问题时,常遇到一些问题直接求解较为困难,通过观察、分析、类比、联想等思维过程,选择运用恰当的数学方法进行变换,将原问题转化为一个新问题(相对来说,是我们熟悉和已解决的问题或容易解决的问题),通过新问题的求解,达到解决原问题的目的,这一思想方法我们称为转化法.

例1图

例1 如图所示,在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30m,至点C处测得顶端A的仰角为2θ,再继续前进至D点,测得顶端A的仰角为4θ,求θ的

大小和建筑物AE的高.

点拨 本题可转化为解三角形的问题,利用正弦定理求解;也可转化为方程问题求解;还能借助二倍角公式解决.

解答 解法一:(用正弦定理求解)

由已知,可得

在△ACD中,AC=BC=30,,∠ADC=180°-4θ.

∵sin4θ=2sin2θcos2θ,解得2θ=30°,∴θ=15°.

∴在Rt△ADE中,AE=ADsin60°=15(m).

答:所求角θ为15°,建筑物高度为15m.

解法二:(设方程求解)

设DE=x,AE=h.

在Rt△ACE中,

在Rt△ADE中

两式相减,得

在Rt△ACE中

答:所求角θ为15°,建筑物高度为15m.

解法三:(用倍角公式求解)

设建筑物高为AE=x.

由题意,得∠BAC=θ,∠CAD=2θ,

AC=BC=30,

在Rt△ACE中

在Rt△ADE中

②÷①,得

则2θ=30°,θ=15°,AE=ADsin60°=15(m).

答:所求角θ为15°,建筑物高度为15m.

反思 将复杂的问题转化为简单问题,通过求解简单问题达到解决复杂问题的目的.本题有多种转化方式,是一题多解的典型问题.

2.基本不等式法

基本不等式是解决最值问题的一种常用方法.在运用基本不等式0)解题时,一定要注意其成立的条件“一正、二定、三相等”,即“正数是前提,定值是基础,相等是保证”,三者缺一不可.

例2 已知A、B、C是△ABC的三个内角

(1)若任意交换两个角的位置,y的值是否变化?试证明你的结论.

(2)求y的最小值.

点拨 第一问要将原式转化为y=cotA+cotB+cotC;第二问的最值问题可利用基本不等式求解.

∴任意交换两个角的位置,y的值不变化.

故当

反思 本题的第(1)问是一道结论开放型题,y的表达式的表面不对称性显示了问题的有趣之处.第(2)问实际上是一道常见题:在△ABC中,求证:cotA+cotB+cotC≥3.

易错解读

易错点 没有进行分类讨论导致错误.(www.xing528.com)

分类讨论思想,就是按照一定的标准,把有关问题转化为几个部分或几种情况,从而使问题明朗化,然后逐个加以解决,最后予以总结得出结论的思想.

例3图

例3 如图所示,有两条相交成60°角的直路EF、MN,交点是O.起初,阿福在OE上距O点3km的点A处;阿田在OM上距O点1km的点B处.现在他们同时以4km/h的速度行走,阿福沿EF的方向,阿田沿NM的方向.

(1)求起初两人的距离;

(2)用包含t的式子表示t小时后两人的距离;

(3)什么时候他们两人的距离最短?

解答 (1)∵AB2=OA2+OB2-2OA·OBcos60°=7,

∴起初他们两人的距离是

(2)设他们t小时后的位置分别是P、Q,则AP=4t,BQ=4t.

下面分两种情况讨论:

当时,PQ2=(3-4t)2+(1+4t)2-2(3-4t)(1+4t)cos60°. ①

当时,PQ2=(3-4t)2+(1+4t)2-2(4t-3)(1+4t)cos120°. ②

由①②,得PQ2=48t2-24t+7,即

(3)∵

∴当时,即在第15分钟时他们两人的距离最短.

反思 本题第(2)小题中,阿福的位置在O点的右侧还是左侧是需要进行讨论的.本题还可以转化为坐标运算,从而避免分类讨论.提示:以O为坐标原点,OE所在直线为x轴建立直角坐标系,则t时刻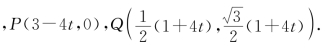

第1题图

经典训练

1.某人要利用无人机测量河流的宽度,如图所示,从无人机A处测得正前方河流的两岸B、C的俯角分别为75°,30°,此时无人机的高是60m,则河流的宽度BC等于(　).

A.

B.

C.

D.

2.如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据得cosθ=_________.

第2题图

第4题图

3.一艘海警船从港口A出发,以每小时40海里的速度沿南偏东40°方向直线航行,30分钟后到达B处,这时候接到从C处发出的一求救信号,已知C在B的北偏东65°,港口A的东偏南20°处,那么B、C两点的距离是_________海里.(1海里=1.852千米)

4.某中学举行升旗仪式,在坡度为15°的看台E点和看台的坡脚A点,测得旗杆顶部的仰角分别为30°和60°,量得看台坡脚A点到E点在水平线上的射影B点的距离为10 cm,则旗杆CD的高是_________m.

5.一人在海面某处测得某山顶C的仰角为α(0°<α<45°),在海面上向山顶的方向行进m m后,测得山顶C的仰角为90°-α,则该山的高度为________m.(结果化简)

6.某老师在校阅试题时发现一道题目:“从60°角的顶点开始,在一边上截取9cm的线段,在另一边截取acm的线段,求所得两个端点之间的距离.”其中acm在排版时比原稿上多了1,虽然如此,答案却不必改动,即题目与答案仍符合,则a=_________cm.

7.某人站在60m高的楼顶A处测量不可到达的电视塔高,测得塔顶C的仰角为30°,塔底B的俯角为15°,已知楼底部D和电视塔的底部B在同一水平面上,则电视塔的高为________m.

8.为了测量正在海面匀速直线行驶的某航船的速度,在海岸上选取距离为1km的两个观察点C、D,在某时刻观察到该航船在A处,此时测得∠ADC=30°,3min后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,则船速为_________km/min.

9.航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10km,速度为180km/h,飞机先看到山顶的俯角为15°,经过420s后又看到山顶的俯角为45°,如图所示.求山顶的海拔高度

第9题图

10.如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李不打算坐索道,而是花2个小时的时间进行徒步攀登.已知∠ABC=120°,∠ADC=150°,BD=1km,AC=3km.假设小王和小李徒步攀登的速度为每小时1200m,则两位登山爱好者能否在2个小时内徒步登上山峰.(即从B点出发到达C点)

第10题图

11.如图所示,某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点A、B,观察对岸的点C,测得∠CAB=75°,∠CBA=45°,且AB=100m.

(1)求sin75°;

(2)求该河段的宽度.

第11题图