总复习不论在哪一个阶段，也不论是哪一种课型，课堂教学均讲究方式方法，讲究效率。一般来讲，从教师和学生所进行的活动来看，不外乎教师讲授、点评、示例，学生讲述、展示、训练、归纳、总结等，可以将其简称为“讲-练-评-例-结”五环节法。
“讲”指讲考点知识的来龙去脉、联系与区别和考纲要求。
“练”指课堂内用10-15分钟时间检查性练习，围绕考点，辨明是非，培养技能，掌握技巧。
“评”指对思路、技巧和基础的理解，从正反两方面进一步深刻揭示，形成完整的认识结构。
“例”指举典型范例分析示范，导其思，引其路，并举错辨误。
“结”是从考法、技巧、思路、题型上加以总结、概括、发掘出规律。
“讲、练、评、例、结”五环节不是一种僵化的结构，而是一种动态的组合，可以有多种模式，例如：“讲-练-评-例-结”“练-讲-例-评-结”“例-练-评-讲-结”等，适合于不同的教学阶段或教学内容。如在考点基础复习课上，一般按照“练-评-讲-例-结”五环节进行教学；在专题讲练课上，一般按照“讲-例-练-评-结”五环节进行教学；在试卷讲评课上，一般按照“练-评-例-讲-结”五环节进行教学。
复习教学案例：平面简谐横波的专题归类复习
教学目标：
1.通过典型习题的分析与讨论，学生能掌握平面简谐横波的传播特征、波与质点振动之间的关系；
2.学生能掌握波的双向性和周期性特点，熟练运用波速公式v=λf=Δx/Δt解决有关计算问题；
3.学生能够熟练运用波的知识，确定质点振动路程、速度等状态，会画另一时刻的波形；
4.通过具体的实例分析，学生灵活运用知识的能力和发散思维能力有较好的发展与提升。
教学方法：“讲-练-评-例-结”五环教学法。
教学重点：波的传播特征及其规律性，v=λf的运用。
教学难点：横波传播的规律性及v=λf=Δx/Δt的灵活运用。
教学过程设计：
一、知识点精讲（边提问边归纳）：
1.平面简谐波是简谐振动这种运动形式和能量在周围弹性媒介中的传播，而质点并不随波迁移。
2.波沿传播方向以速率v=λf匀速迁移，而传播方向上的各质点只在各自的平衡位置附近作同振幅、同周期而不同相位的简谐振动。
3.波在一个周期的时间内，沿传播方向迁移一个波长的距离，其中的质点完成一次全振动，通过4A路程。
4.t时刻的波形与nT±t时刻波形相同。沿+x传播
距离时的波形与沿-x轴传播
距离时的波形相同。
图一
二、形成性题组练习
1.如图一所示，有一列沿-x轴方向传播的横波，那么M点此时的运动方向如何？若此列波的波长为0.4m，波的振幅为5cm，再过
的时间M质点在何处？
图二
2.某横波在x轴上传播，波速为5.0m/s，已知t=0时刻的波形如图二，且M点的运动方向已标出，那么此时P、Q点的运动方向如何？
3.在图二坐标系中画出再过0.5s时的波形图。
4.如图一为t=0时的某横波，波速为v=2m/s，在t=0到t=2.5s时间内，质点M通过的路程是多少？此时的位移是多少？
三、反馈矫正——评析（逐题评析，指出思路，找出关键）
1.t时刻的波形、波的传播方向和该时刻质点的振动方向之间，构成相联系的一个整体，给定其中的两个，第三个便是可唯一确定的。波的传播方向和振动方向（质点）的确定，可用波形平移法或半波形内三角形旋转法来判断。在Δt时间内波沿传播方向平移Δx=vΔt的距离，而质点并不随波迁移。M质点此时向上振动，经过
后M点的坐标为（0.2m，-5cm）。
2.由t时刻的波形画出t+Δt时刻的波形，首先要知道波的传播方向，沿传播方向将原波形平移Δx=vΔt的距离。当时间较长时，可把Δx化成
Δλ+nλ的形式，只要将波平移Δλ距离即可。
3.求某质点在一段时间内振动的路程，关键是要把Δt时间化成
的形式，那么质点在Δt的路程即为
。
以上分析要求学生掌握波的整体性、周期性和4A性等规律，使学生认识到某种物理现象的变化发展有其自身的规律，掌握了规律，此类题即可迎刃而解。
四、范例分析，归纳思路方法
例题：如图三，实线是一列简谐横波在t时刻的波形曲线，虚线是再过0.2s时的波形图，求：
图三
（1）这列波的传播速度多大？
（2）若T＜0.2s，v=45m/s，求波的传播方向。
（3）若波沿+x轴传播，t时刻P、Q二点的运动方向如何？
（4）若v=5m/s，质点P在2s内通过的路程多大？
（5）本题中，若v=10m/s，求可能的波长。
（6）评论或练习：本题中若实线为波在某时刻的波形，虚线为波沿x轴传播了0.2米后的波形，已知v=8m/s，则波可能的频率为多大？
引导分析与讨论：
（1）λ=4m，未说明波的传播方向，故有两种可能性：波沿+x或-x轴方向传播。限制了时间，可以写出可能的周期，可用v=λ/T或v=Δx/Δt两种方法来求v。(www.xing528.com)
方法一：波沿+x轴传播时，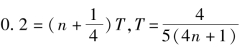
所以，v=λ/T=5（4n+1）m/s，n=0，1，2……
波沿-x轴传播时，
所以，v=λ/T=5（4n+3）m/s，n=0，1，2……
方法二：波沿+x轴传播时，Δx=nλ+1=4n+1
所以，
波沿-x轴传播时，Δx=nλ+3=4n+3
所以，
（2）从t时刻与t+Δt时刻波在空间和时间两个角度分别分析，波长和周期的关系来判断。也可用假设法确定n，n必为整数，否则假设错误，波必沿反方向传播。
方法一：由
知，波向右传。
方法二：由
知，波向右传。
方法三：假设波向右传，应
故此波必向右传。
方法四：假设向左传，应
假设不成立，此波必向右传。
（3）可用三角形旋转法判定（略）。
（4）因为
所以
（5）方法与思路同（1）。
若左传，
由λ=vT
所以λ=8/（4n+3）m；n=0，1，2……
若右传，
由λ=vT
所以λ=8/（4n+1）s；n=0，1，2……
6）向左传时f=10（4n+3）Hz n=0，1，2……
因为，Δx=0.2mV=8m/s
所以，左传时，
，由
同理得，向右传时f=10（4n+1）Hz n=0，1，2……
五、小结归纳
1.知识点——四性一律（略）
2.方法思路
（1）“三态一体”：质点的振动状态、波的传播状态和波在该时刻的形状三位一体，具有瞬时性、整体性特点。
（2）“三量一式”：波长λ、波速v和周期T是表征波的三个基本特征量，它们之间的关系是v=λ/T。
（3）“三类问题”：波的问题，不外乎波形状态与波的传播方向、波传播快慢与传播距离和时间、质点振动状态问题这三类。
六、作业布置
1.一列沿直线传播的横波，在传播方向上相距S的两质点a、b均在平衡位置，已知振幅为A，ab间只有一个波谷，试画出可能的波形图。
图四
2.一列横波在t=0时的波形如图四所示，波速为1.5m/s，经过多少时间质点P第一次到达波谷？
教学反思：
第一，本节课容量大，时间紧，应尽可能在前一段知识精讲过程中节约时间，保证在例题讨论中有充足的时间，促进学生发散思维。
第二，例题中的（3）、（4）两问可留作课内外练习，（6）问也当作课堂练习或在课外完成。
第三，要突出思路与方法的引导。
板书设计：
平面简谐波的归类专题复习
平面简谐横波的特征与规律：
①波是振动形式和能量的传播，质点并不迁移。
②波以v=λf速度匀速迁移，Δx=vΔt，各质点均作简谐运动。
③波在T时间内迁移λ距离，某质点通过4A路程。
④t时刻的波形与nT±t时刻波形相同，经过Δt时间和经过nT±Δt时间的波形相同。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
