【摘要】：思维从问题始,疑是思维的起点。“疑者,觉悟之机也。”教学中不仅要注意克服思维定势产生的负迁移,而且要大力提倡质疑和敢于科学否定的精神。从矛盾的对立面进行思考,产生丰富的相悖论概念,联想相反的事物,是培养逆向思维能力的有效途径。因此,可引导学生把问题颠倒过来考虑。把一种不定值问题用逆向思维的方法转化为定值问题,达到了速解、巧解的目的。
思维从问题始,疑是思维的起点。“疑者,觉悟之机也。”教学中不仅要注意克服思维定势产生的负迁移,而且要大力提倡质疑和敢于科学否定的精神。在解决物理问题时,要启发学生多联想,发散性思考。顺推不行就逆推,正面不易解决就考虑从反面入手,直接解决不了就考虑间接解决,解决问题的可能性有困难就考虑解决问题的不可能性,用已知命题无法解决时就换另一种与其等价的命题解决……从矛盾的对立面进行思考,产生丰富的相悖论概念,联想相反的事物,是培养逆向思维能力的有效途径。
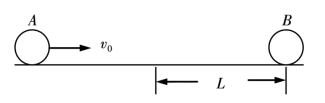
图4.4
例题3:如图4.4所示,在光滑水平轨道上有两个半径都是r的小球A与B,质量分别为m和2m。当两球心间距大于L(L比2r大得多)时,两球之间无任何作用力;当两球心间距离小于或等于L时,两球间存在相互作用的恒斥力F。若A球从远离B球处以初速度v0沿两球心连线向原来静止的B球运动,欲使两球不发生接触,v0必须满足什么条件?
分析:此题本身就是按逆向思维方式命制的,属于“欲达到……结果,条件……应如何”的类型。因此,可引导学生把问题颠倒过来考虑。假若两球刚好接触,则A与B的相对位移为L－2r,对系统根据功能原理得:
又,系统动量守恒:mv′0=(2m+m)v
解得: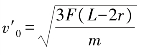
故,欲使二球不接触,则须。再把问题颠倒回去,便很轻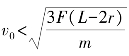
松地找到了答案。把一种不定值问题用逆向思维的方法转化为定值问题,达到了速解、巧解的目的。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
