结构蒙特卡罗模拟法详解：理解蒙特卡罗模拟策略

“蒙特卡罗”名字取自1862年建立的位于法国南部的著名赌场。可见随机模拟法与赌博业的渊源很深。在金融与证券市场的研究中，大家常常利用蒙特卡罗法模拟出投资组合在指定日期的各种不同价格走势，然后根据由这些模拟价格导出的投资组合在指定日期的价格分布，最后从分布中自然地解读出投资组合的VaR值。可以说蒙特卡罗的适用性很强，应用极其广泛，所以它是计量投资组合VaR值的最有效、最强大的工具。它可以计量风险的范围，包括市场风险、信用风险、波动率风险等，甚至还能够度量最为隐蔽的一种风险：模型风险。“蒙特卡罗”的基本思路是：重复多次地模拟金融变量的随机走势，以求涵盖其各种各样的价格变化情况。所以随机模拟的过程就是重塑投资组合价值分布的过程。在数量工具章节中，我们已经介绍过有关的技术细节与应用方法，所以本节不做更详细的技术分析。

（1）单风险因子的蒙特卡罗模拟

我们从单风险因子入手，展示如何应用蒙特卡罗模拟法计量VaR。基本步骤如下：第一步，确定风险因子及其服从的随机过程。第二步，计算机模拟风险因子的未来走势。第三步，确定未来某一个交易日的风险因子分布情况。第四步，根据风险因子的分布确定资产的价值分布，由此确定VaR值。

我们以投资某只股票为例，按部就班地计算VaR。假设我们的目标是计量持续期为10个交易日的VaR。

第一步：股票价格服从几何布朗运动d St＝μStdt＋σStdzt，其中dzt服从均值为0、方差为dt的正态分布。我们用Δt来近似替代微分变量dt，于是ΔSt＝St－1（μΔt＋σε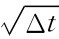），其中ε服从均值为0、标准差为1的标准正态分布。

我们模拟10个交易日的股票价格情况，并且每一天的模拟次数达到500次，当然可以更多。

在得到第10个交易日的股票资产价值变化后，利用菜单“工具”→“数据分析”→“排列与分位数”获得损益数据的分布情况，最后再次利用Excel的Vlookup（）函数求得95％置信水平的VaR值。根据计算结果，我们有99％的把握得出以下结论：30 000元的股票投资（30×1 000），10个交易日后的最大损失不超过2 877元。

我们需要强调的是，蒙特卡罗模拟中选择的随机模型若是与实际价格走势不符，那么据此计算出的VaR也不可信，所以随机模型的确定极其重要。

（2）多风险因子的蒙特卡罗模拟

我们把上面的问题深入一步，现有投资人投资于两只股票，假定这两只股票分别服从所谓的几何布朗运动：

图9．62(www.xing528.com)

图9．63

且和具有相关性cc。若相关系数不等于0，那么在模拟生成股价的时候，随机数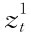和就不能够独立变化了。下面我们首先验证一个事实：

令：，其中ε1与ε2互相独立，那么，

Var（z2）＝ρ2Var（ε1）＋［（1－ρ2）1／2］2Var（ε2）＝1，且

Cov（z1，z2）＝Cov（ε1，ρε1＋（1－ρ2）1／2ε2）＝ρCov（ε1，ε1）＝ρ

我们发现经过变换之后，由两个独立的随机变量得到了相关系数为ρ的两个随机变量，这正是我们想要的。在下面的Excel表中，给出有关模型参数。

图9．64

我们要求计量1天的VaR值，置信水平为95％，A4：F6中存放基本信息资料，而在D列和E列中给出的是互相独立的随机正态变量，F列和G列计量的是在给定相关性系数为0．5的情况下1天之后的股票A和B相应的模拟价格。H列给出的是1天之后投资组合的价值变化值，然后利用菜单“工具”→“数据分析”→“排列和分位数”工具得到J列和K列的排列结果，最后再次借助Vlookup函数寻找到95％分位数对应的组合VaR值。

我们留给读者两个问题：（1）请尝试建立三个股票组合的VaR值计量模板，请回顾在数量工具章节中介绍过的实对称矩阵的Cholesky分解技术，考虑如何利用该技术获得多风险因子的带有相关性的随机数据模拟。（2）自定义函数。输入变量是股价、波动率、飘移率、终止日、模拟次数等必要参数，输出变量是一定置信水平下的VaR值，并将该函数扩展到多股票组合情形。