参数分析法：详细解析与应用

（1）单个风险因子的Delta－Normal VaR

对于单一的风险资产，应用Delta－Normal VaR计量风险相对比较容易。以股票风险资产为例，假定100万美元投资于某股票A，并假设其收益分布服从正态分布，那么只要知道了该分布的均值与方差，我们就可以得到在给定时间长度及置信水平下所谓的Delta－Normal VaR值。我们在Excel中建立相应的模型，通过选择不同的分析参数来计算有关VaR值。

该模型分成三个模块。第一个模块在A5：E9中对计算参数进行设定，包括时间长度、置信水平、置信的单双尾（通常计量VaR都讲单尾），而第9行中计算的是在给定正态分布假设和置信参数下的左侧分位数（我们保留了负号），应用了标准正态分布的逆函数NORMSINV。

A11：E13中记录的是分布的有关参数、均值和标准差。A15：E16计算了相对VaR值和绝对VaR值。所谓相对VaR值是指忽略持有期内的收益率，而绝对VaR值考虑持有期内的收益率，在其他条件相同而时间长度较短的情况下，两者的差异并不大。但若时间长度较长或收益率相对于波动率较大，那么两者差异就会有所显现。用数学公式表达如下：

图9．49

Relative VaR＝－zα×σ××P

Absolute VaR＝（r×t／T－zα×σ×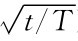）×P

留给读者一些问题：在我们已经做好的模型基础上，请进一步完善模型，例如考虑其他的分布函数，并且允许用户选择不同的分布假设，并自动计算出给定分布下的有关VaR值。

（2）投资组合的Delta Normal VaR

投资组合就是对一定数量的风险因素持有量的组合。当把它进行分解后，投资组合的收益就是各种基础资产收益的线性组合，每种资产的权重由最初对该资产投资的金额决定。于是投资组合的VaR可以由其所包含的各种有价证券的风险组合得出：

Rp ，t＝，这里的权重系数wi，t在最初t时刻的起初就得以确定，其和为1。于是我们可以得组合P的均值和方差的表达式：

该表达式不仅说明了个别证券的风险，而且也说明了任何两个不同资产交叉项的风险，总共有N（N－1）／2个不同的协方差。随着风险因子的数量增加，把所有的协方差都写下来显得很困难，此时采用矩阵的方式就会简单得多。用矩阵表示的方差为：

记上式中间的协方差矩阵为Σ，于是投资组合的方差可以简写为：。同样的，我们采用Delta－Normal的方法计量VaR值。在Excel的应用中，最核心、最关键的就是如何求得协方差矩阵Σ。我们采用历史数据来估计股票收益率的波动率情况。

图9．50

单元格K6：S104中存在的是8只股票的历史每日收益率数据。

我们运用了在市场风险度量章节中自定义的求解协方差矩阵的函数VCV（）求解该给定8只股票资产的每日协方差矩阵，同时估计出它们的每日收益率的均值。根据σ2p＝ῶ′Σῶ，利用MMULT（）的矩阵乘积函数得到组合的总方差及标准差。接下来的步骤就与上一节单个风险因子的Delta－Normal VaR的计算过程类似了，只是在计量VaR时小心应用平方根法则来求解10天的VaR值，并比较相对VaR与绝对VaR的差异。

（3）风险因子映射技术（Risk Mapping）

对那些只投资于原始因子（例如股票、零息债券、外汇、商品等）市场的投资组合而言，VaR可以通过所投资的因子的协方差矩阵和头寸的向量直接进行计量。事实上，第（2）节中就是直接投资于股票风险因子的资产组合。而在更多的场合中，投资组合包括更为复杂的资产。我们通过所谓的风险因子映射技术将证券分解成与原始风险因子相对应的含有Delta系数的资产组合，然后利用原始风险因子各自的波动率来估计投资组合的VaR值。我们通过两个例子来分析如何进行风险因子的映射：

第一个例子：当前有一个简化的零息债券剩余到期日为2．75年。我们希望能够生成两股现金流，一个是2年到期，另一个3年到期，并且分解后的组合风险与原来的零息债券风险等价。

这里所谓的风险等价即指无论2年期或3年期的即期利率发生任何微小变化，分解后的组合的现值变化与原来的组合现值变化相同，也就是两者的。

在这个例子中，我们对于在2年与3年之间的即期利率采用了线性插值（Linear Interpolate）的方法，在这个方法下我们假设无论2年期或3年期的利率如何变化，分解后的组合现值变化与原来的债券价值变化相同。但需要注意的是，满足以上条件，并不代表分解的两个债券的价值之和等于被映射的债券。单元格F14：F15计量的就是分解出的两个债券到期现金流。C8：D8计量的是这两个债券的现值（PV），很明显其与B8中原始债券的现值不同。

第二个例子：比前一个例子更为复杂一些。我们有某个债券投资组合，有较多不同期限的现金流。我们的问题是：如何求解得到风险等价的零息债券投资组合？方法上应当与前一例子相同，只要将原始债券投资组合的现金流根据到期日进行汇总，每一个到期现金流均可以风险等价地分解为其相邻两个风险因子的现金流组合。在Excel中的应用，需要我们设计一个较好的、较直观的模型。

图9．51

图9．52(www.xing528.com)

图9．53

操作思路是这样的：例如对于Bond 2，其到期期限为3．6年，那么就应当确定要分解映射的风险因子是相邻的两个期限，即3年和4年，然后确定到对应的单元格D11：D12中，按照第一个例子中的算法求得风险等价的两股到期现金流（即对应零息债券面值）。为了在Excel中处理方便起见，我们自定义了风险因子映射的函数，面对较为复杂的且难以利用Excel固有的格式批量完成的问题，读者应当熟悉并练习自定义函数解决。Risk Map的具体代码如下：

Function Risk Map（principle，mapped＿maturity，map1＿maturity，map1＿rate， map2＿maturity，map2＿rate）

Dim mapped＿rate As Double，mapped＿temp As Double，cash（1To 2，1To 1） As Double

mapped＿rate＝（（map2＿maturity－mapped＿maturity）＊map1＿rate＋（mapped＿maturity－map1＿maturity）＊map2＿rate）／（map2＿maturity－map1＿maturity）

mapped＿temp＝（（map2＿maturity－mapped＿maturity）＊（map1＿rate＋0．0001）＋（mapped＿maturity－map1＿maturity）＊map2＿rate）／（map2＿maturity－map1＿maturity）

cash（1，1）＝（principle＊Exp（－mapped＿rate＊mapped＿maturity）－principle＊Exp（－mapped＿temp＊mapped＿maturity））／（Exp（－map1＿rate＊map1＿maturity）－Exp（－（map1＿rate＋0．0001）＊map1＿maturity））

mapped＿temp＝（（map2＿maturity－mapped＿maturity）＊（map1＿rate）＋（mapped＿maturity－map1＿maturity）＊（map2＿rate＋0．0001））／（map2＿maturity－map1＿maturity）

cash（2，1）＝（principle×Exp（－mapped＿rate×mapped＿maturity）－principle×Exp（－mapped＿temp×mapped＿maturity））／（Exp（－map2＿rate× map2＿maturity）－Exp（－（map2＿rate＋0．0001）×map2＿maturity））

Risk Map＝cash

End Function

通过以上的两个例子，我们已大致了解如何进行风险因子的分解与映射。我们接着看第二个例子，来为大家展示如何进一步计量投资组合的VaR。本质上和第（2）节的方法相似，只不过这里的组合换成了零息债券。对于零息债券而言，其风险因子可以确定为到期收益率，也就是所谓Spot Rate。零息债券的价格变化率与spot rate的变化之间仅仅差了一个久期，而零息债券的久期几乎可以近似地用到期日来替代。

理论上，零息债券的投资组合的价格波动可以表示为：

其中，Bi代表零息债券的现值，Di代表债券的久期，yi代表对应的Spot Rate。若dyi服从正态分布，那么其线性组合后的d（P）也服从正态分布。经过这样的分解，我们发现就和股票投资组合的情况完全相同了。为了估计d（P）的波动率，则只要估计dyi的波动率及不同dyi之间的相关性矩阵Σ，然后乘以对应置信水平的关键系数并调整持续期即可。

VaR（d P）2＝［B1D1VaR（dy1），…BNDNVaR（dy N）］（ε）

［B1D1VaR（dy1），…BNDNVaR（dy N）］′

该VaR值的持续期与dyi的期限相同。下面的Excel表格中，我们基于风险因子分解的结果计量了原来债券组合的VaR值。

图9．54

（4）Delta－Gammar近似方法

Delta－Normal法的最大缺陷就是除了Delta线性风险外，忽略了所有其他的风险类型。对于期权（我们以欧式看涨期权C为例）这样的具有非对称支付函数的金融工具而言，若是希望捕捉到Gammar二阶风险，则可以在其泰勒展开式中将对应的风险项列出：

其中的Δ、Γ是总的期权投资组合的净值，而且这些期权是针对同一项基础资产的。同时，期权组合对应的VaR值由下式确定：

可见当期权组合的Γ净值大于零时，有缓释VaR值的作用；反之，若Γ净值小于零，则增加VaR值。

图9．55