详解925信用评级模型：定义、特点和应用

金融机构通过内部或外部评级（rating）来表征贷款人的信用质量。一些公开的专业评级机构使用“字母”来做信用评级，这样的公司有S＆P，Moody，Fitch等。有了信用评级之后，我们还希望能够将这些字母定量地映射到违约率上。在这方面，有一些比较成熟的方法或工具可以应用，如信用迁移矩阵、打分卡评级模型、Logistic模型和probit模型、Merton＆KMV模型、市场隐含违约率模型等。我们将分别介绍如何在Excel中应用它们，其中将用到一些数量分析工具，如矩阵的应用、多元线性回归、期权定价模型等。

（1）信用迁移矩阵的应用（Credit Migration Matrix）

转移矩阵给出的是在某一段时间内，债券发行人或贷款人从一个信用等级迁移到另一个信用等级的概率信息，通常记为P＝（Pij），其中Pij表示从i等级迁移到j等级的概率，这样的矩阵一般并不对称，例如从AAA级降级到AA的概率与AA级升到AAA级的概率并不一致。在多个时间段情况下，我们总是简单地假设目标机构或个体的信用变化满足马氏规则，即下一期的信用等级仅与当前的信用等级相关。于是通过转移矩阵，我们就可以得到任意长度期限内的转移矩阵，也即信用变化信息，更妙的是由此还能够得到违约期限结构。表9．4给出了一年实际平均信用转移矩阵：

表9．4

在表9．4中，我们可以看到，从AAA到BB的概率为0．19％，而从BB到AAA的概率为0．04％。我们的问题通常是给定这个转移矩阵，如何获得三年内某评级为AA的公司的信用等级信息。这可以通过矩阵乘积的方式求得，下面我们在Excel中展示，其中应用到了数量工具章节中介绍的矩阵应用等基本函数。

在C16：J23中存放的是两年内的信用等级迁移矩阵，而C27：J34中计算的是五年内的信用等级迁移矩阵，运用到了我们在数量工具章节中自定义的矩阵幂函数，函数程序重新表述如下：

图9．30

Function Matrix Power（Matrix As Range，p As Integer）

Dim n As Integer，i As Integer，j As Integer，E（）

n＝Matrix．Rows．Count

Select Case p

Case－1

Matrix Power＝Application．Worksheet Function．MInverse（Matrix）

Case 0

Re Dim E（1To n，1To n）

For i＝1To n

E（i，i）＝1

Next i

Matrix Power＝E

Case Else

Matrix Power＝Matrix

For j＝1To p－1

Matrix Power＝Application．Worksheet Function．MMult（Matrix Power， Matrix）

Next j

End Select(www.xing528.com)

End Function

我们留给读者一个问题：若是已知1年的信用迁移矩阵，如何求得更短时间内的信用迁移矩阵，例如半年，或者1个月等。这是先前问题的反问题，在代数上实际上是要求求解矩阵的N次根的问题。

（2）打分模型（Scoring model）

打分模型的思路是：通过给贷款人打分的方式来进行贷款评级，分数高的人信用质量较高。该模型最早是由Altman（1968）发明的。如此的信用打分模型通常依赖于一些会计数据，类似于EBIT／Total Asset（息税前收益／总资产）、Sales／Total Asset（总资产周转率）等。Altman认为，应使用如下的打分模型来为贷款机构进行打分：

其中，

于是我们可以根据以上的打分模型来给所有的贷款机构进行信用打分，然后根据分数进行排序。分数越高，其信用质量越高。同时，Altman经过统计分析后给出了一个分界点1．8，即若打分值小于1．8，则借贷人违约的可能性很大，贷款应当拒绝。我们通过Excel举例说明如何应用该模型来为贷款进行决策。

图9．31

表格中的计算都是直接的，值得注意的几个技巧是：其一，H13：H22的打分结果应用了MMULT函数，读者需要熟悉向量乘积这种方法（而非通常的简单加和公式）；其二，I列存放了按照打分高低的排名，最高分列第1名，依此类推。在具体计算时有多种方法：

方法一，在空白处将打分进行降序排列，然后在旁边一列给予1－10的排名，最后利用Vlookup函数来填写Rank一列的排名。

方法二，见如下分解：

第一步：将打分值编号（尚未排名）。

第二步：选择菜单中的“数据－＞排列”，参数改为value列，Desceding降序→OK确定。

图9．32

图9．33

第三步：根据value列从高到低在rank列中进行排名。

图9．34

第四步：选中no、value、rank三列数据，再按照no升序排列，得到最终所要的结果。

图9．35

图9．36

（3）Logit ＆Probit模型

对于Probit模型，它假定贷款人的违约率可以写成pi＝ψ（β0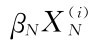＋＋…＋），其中ψ（·）是正态分布的累计分布函数，βi是统计估计参数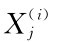，是一些可以解释违约率的会计比率。该模型和Scoring模型类似，但不同的是：打分模型中分数越高，违约率越小，但在Probit模型中，恰好相反。

Logit模型和Probit模型的唯一不同之处在于：Logit模型并不使用正态分布的累计分布函数将打分对应到违约率，而是使用Logistic函数，即：

本质上，Logit和Probit模型与Scoring模型并没有多大区别，所以应用Excel的过程是完全类似的。