单指数模型是现代金融理论中最早被采用，并且已被事实证明是较好地反映了实际市场情况的一种假设。单指数模型的最基本假设是：证券收益之间的变化主要是由于其受到同一因素的影响。单指数模型认为，各证券收益间之所以具有联系是因为它们对市场变化有共同的反应，对这种共同反应较好的表示方式是把单个股票收益和股票市场指数的收益联系起来。通常，我们选择的股价指数是将所有股票或几个最主要的，最具有影响力的股票组合起来得到的平均加权水平，并根据该指数的变化确定收益率，一般用M表示市场指数。
图6．14
单指数模型基本方程：Ri＝αi＋βiRm＋εi，其中，Rm是市场指数的收益率，为随机变量；Ri是第i个证券的收益率，为随机变量；εi是残余项。单指数模型表明个股在某阶段的收益率与同期到市场指数的收益率在统计上存在线性相关关系，由于线性回归模型存在较强的假设，因此单指数模型必须满足一系列假设条件：
①随机残项的期望值为零，即E（εi）＝0；
②Cov（Rm，εi）＝0，该假设认为市场指数的变化与个股的特定风险无关；
③Cov（εi，εj）＝0，i≠j。该假设最为关键，它说明Ri和Rj之间的相似变化，不是由于其他影响因素，而是由于Rm的影响所致。(www.xing528.com)
在单指数模型的基本假设下，我们可以得到单个证券及组合的期望收益率与风险度量。
对于单个证券：E（Ri）＝αi＋βiE（Rm），
对于证券组合P：E（RP）＝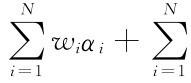
wiβiE（Ri）≜αP＋βPE（Rm），
在以上的最后一项式子中
就是组合总风险中的系统风险，而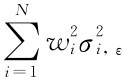
就是组合的残余风险，可以证明在组合中资产个数大幅上升后，残余风险将趋于零，也就是通过组合后被几乎完全分散掉。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
