麦考利久期度量了债券现金流的平均偿还时间。麦考利久期越长，债券对利率的敏感度越高。如果仅到此为止，麦考利久期也不会有如今这样的地位。事实上，除了是一个平均时间的度量，麦考利久期有着更为重要的意义。
设债券的价格为P，收益率为y，一年付息k次，n年到期。我们有如下等式：
其中的∑都是将i从1到n＊k求和。
那么，
将上式稍作变换，得到
这里，我们引入另一个久期的概念：修正久期（Modified Duration），记做MD。修正久期定义为麦考利久期除以1加上期限收益率，即
最后，我们得到
这个公式说明了：债券价格变化的百分比等于收益率的变化量乘以负的修正久期。
如果收益率为连续收益率，那么修正久期等于麦考利久期。
修正久期的几何意义：
设债券价格为P，收益率为y，作Log（P）关于y的函数图像。取Log（P）是因为Log（P）的变化量等于P的变化的百分比，所以我们有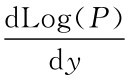
＝－MD。从图形上来说，－MD就是函数图像的斜率。
图5．20
计算修正久期的函数如下：(www.xing528.com)
Function MD（Coupon Rate As Double，n As Integer，k As Integer，yield As Double）
MD＝MCLD（Coupon Rate，n，k，yield）／（1＋yield／k）
End Function
【例5．7】 （用久期测度的债券价格变化）
假设一个债券本金为100，票息率14％，15年后到期，一年付息两次，现在以10％的收益率发行，我们将考察当收益率发生变化时债券价格的变化。
图5．21表示了这个模型。我们首先将数据输入A1到B5区域，并且定义单元格名称B1为“PRN：”，B2为“CR”，B3为“n”，B4为“k”，B5为“y”。B7中计算这个债券的麦考利久期，公式为“＝mcld（CR，n，k，y）”，B8中计算修正久期，公式为“＝MD（CR，n，k，y）”，B10中计算债券价值，公式为“＝bond（PRN，CR，n，k，y）”。
我们在D列中输入一系列收益率。E列计算的是收益率的变化量，我们是以10％作为基准的。F列计算的是用久期衡量的债权价格的变化百分比，根据这个百分比算出收益率变化后债券的价值。H列中计算在相应的收益率下债权的理论价值。I列计算G列和H列的差。E2到I2的公式如图5．21所示。
图5．21
观察I列，我们可以发现，当收益率变化幅度不大时，由久期测度的价值接近于理论价值。但是，当收益率变化幅度较大时，由久期测度的价值就与理论价值相差较大。我们也可以通过图5．22看到这一点。
可见，当收益率发生变化时，单纯地用久期来衡量债券价格的变化可能不够精确。为了更加精确地度量这种价格的变化，我们又引入凸度（convexity）的概念。
图5．22
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
