资本资产定价模型(CAPM)详解

在财务金融学中，一个被广泛接受的权益资本成本估计模型为资本资产定价模型（CAPM）。它是财务学形成和发展中最重要的里程碑，它第一次使人们可以量化市场的风险程度，并且能够对风险进行具体的定价。

该模型是基于风险资产的预期受益均衡基础上的预测模型，马克维茨（Markowitz）于1952年建立现代资产组合管理理论，12年后，威廉·夏普（Willianm F．Sharpe）、约翰·林特纳（John Lintner）与简·莫辛（Jan Mossin）将其发展成为资本资产定价模型，因此该模型又被称为夏普 莫森 林特纳模型。

从20世纪60年代CAPM模型被提出至今，在理财方面其仍有着重大的指导意义。虽然其他模型也试图把握市场行为，但资本资产定价模型因其简洁明了的概念而在实践中被广泛应用。该模型表明所有风险资产的均衡收益率是它们与市场投资组合协方差的函数。

资本资产定价模型的研究对象是在充分组合情况下，风险与要求收益率之间的均衡关系。资本资产定价模型可用于回答如下不容回避的问题：为了补偿某一特定程度的风险，投资者应该获得多大的收益率？

该模型将资产的总风险分为两部分：系统风险和非系统风险。前者是不可化解的风险，是投资者在持有一个完整充分的投资组合之后仍需承受的风险，表示资产与经济的协方差风险测量；后者又叫做可化解风险，或特有风险，是通过投资组合可以化解的风险，表示独立于经济的风险测量。

总风险＝系统风险＋非系统风险

通过构造投资组合，可以消除资产的非系统性风险，系统性风险却不易消除。

CAPM模型有一系列假定条件，在这里我们仅对该模型做一简单介绍。因此，不再一一列举其假定条件。总之，这些基本假定的核心是尽量使个人相同化，而这些个人本来是有着不同的初始财富和风险厌恶程度的。

CAPM模型认为β系数是度量一种证券对于市场组合变动的反映程度的指标，其定义如下：

式中，Cov（Ri，RM）为第i种证券的收益与市场组合收益之间的协方差；

σ2（RM）为市场组合收益的方差。

β表明了单个股票超额报酬率对市场组合超额报酬率的敏感程度。当某只股票的β等于1时，表明该股票与整个市场具有相同的不可避免风险（系统性风险）。当β大于1时，表明该股票的系统性风险大于整个市场的系统风险，因此通常把这类股票投资称为“进攻型投资”。当β小于1时，表明该股票的系统性风险小于整个市场的系统风险，因此通常把这类股票投资称为“防御型投资”。

接下来我们给出资本资产定价模型计量单个证券期望受益的公式：(www.xing528.com)

式中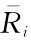，为某种证券的期望收益；

RF为无风险资产收益；

β为证券的贝塔系数；

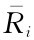－RF为市场的风险溢价。

它表明某种证券的期望收益与该种证券的贝塔系数线性相关。由于长期看来，市场的平均收益要高于无风险资产收益率，因此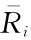－RF应是个正数。所以，更确切地说，某种证券的期望收益与该种证券的贝塔系数线性正相关。

图4．23

上式就是图4．23中的那条斜率为正的直线。值得注意的是，当β＝1的时候，直线从RF至。这条线通常又被称为“证券市场线”（security market line，SML）。

因此，根据上述模型，权益资本成本ks就由公司的系统风险决定。

ks＝Ri＝RF＋β×（RM－RF）

根据上述模型，倘若我们欲计算权益资本成本，就应选取适当的无风险收益率，计算预期市场风险溢价并估算公司的β。该模型假定权益的机会成本等于无风险证券收益率加上公司系统风险（β值）与市场风险价格（市场风险溢价）的乘积。

正如罗斯（Ross，1978）所言：“CAPM模型不仅解释了资产价格，而且为较高的收益总要伴随较大的风险（斯密，卡尔文）直觉提供了分析基础。资产风险溢价不取决于资产的总风险，而取决于资产与整个市场的关系。既然从总体上说，所有的风险都是由于市场投资组合而引起的。只有资产与市场投资组合的关系β，才能决定资产的溢价。”