基本矩阵运算：2x2矩阵详解

（1）矩阵的输入与定义

在单元格中按照矩阵的格式依次输入矩阵的数，然后通过“右击”—“定义名称”—“新建名称”。举例说明：假定现有矩阵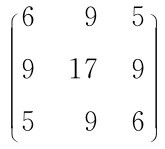，要求将其输入到工作表中，并定义为A。

第一步：在工作簿的工作表中的A1：C3依次输入矩阵中的数字。

第二步：利用鼠标选中单元域A1：C3，依次按键盘Alt I—N—D，出现如下图片框（图2．26），在“名称”中输入A，按“确定”键。

图2．26

图2．27

矩阵在Excel中不能进行符号运算。所谓符号运算就是代数运算，简单地说就是在矩阵的运算公式中含有未确定的变量（Mathematics5．0是符号运算专家， Matlab也可以进行符号运算，但是更加偏重于数值运算）。

（2）矩阵的转置

矩阵一般有m行n列，转置之后变成了n行m列。矩阵转置的函数是：Transpose（array）。

举例说明：假定现有矩阵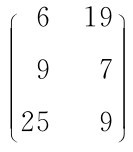，要求获得其转置矩阵。

方法一：公式法

第一步：在A1：B3中输入该矩阵；

第二步：选定A5：C6，输入＝Transpose（A1：B3），然后按Ctrl＋Shift＋Enter。

方法二：复制粘贴法

第一步：在A1：B3中输入该矩阵；

第二步：选定A5：C6，复制—定位在A5—选择性粘贴（在“转置”选项中打勾）以前人们通常使用的是方法二。在高级金融建模中，我们认为方法一更能体现出Excel的高级应用，相对而言更加快捷。在公式法中，有时候对需要进行转置的矩阵，我们定义了一个名称A，那么在后续的公式中我们只需输入＝Transpose （A），然后再按Ctrl＋Shift＋Enter。我们今后对于这样的矩阵名称的替代不再加以说明，读者应该熟练运用。

（3）矩阵的加、减运算

在预先设定好两个矩阵A和B的前提下，只有当他们的Size完全相同的时候才能进行加减运算，运算的结果也是一个矩阵，而且Size和A及B相同。这里的Size是指矩阵的行数和列数，即m×n。(www.xing528.com)

（4）矩阵的行列式

矩阵函数：MDETERM（array）。矩阵的行列式计算是矩阵应用中最重要的运算之一，读者需掌握并牢记相应的矩阵函数。补充说明一下，只有方阵才能进行行列式运算，所谓方阵就是行数和列数相同的矩阵。行列式的最终结果只是一个数，而不是一个矩阵。

（5）矩阵的逆

矩阵函数：MINVERSE（array）。矩阵的行列式计算是矩阵应用中最重要的运算之一，读者需掌握并牢记相应的矩阵函数。补充说明一下，只有方阵才能进行逆运算。逆运算的结果还是一个方阵，Size与原矩阵相同。

（6）矩阵相乘

矩阵之间的乘法和矩阵的数乘是两个概念，初步学习的读者应该对此注意区分。我们将分别进行介绍。两个矩阵相乘必须符合一定的条件，A（m1×m2）， B（n1×n2），那么A×B可以进行的条件是m2＝n1，同样B×A可以进行的条件是n2＝m1。若A和B都是方阵，那么只要它们的阶数是相同的，A×B、B×A自然都是合法的，但结果通常是不一样的。更多的代数知识，我们这里不做介绍和分析。

矩阵相乘的函数是：MMULT（array1，array2）。举例说明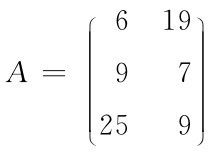：，B＝AT，要求计算B×A。

第一步：首先我们在计算前需要确定B×A后的Size应该是2×2；

第二步：选择一个2×2的空白区域，输入＝MMULT（A，B），然后按Ctrl＋Shift＋Enter。

两个矩阵相乘要预先判定结果的行数与列数，只有在选定好正确的行数与列数下才能得到正确的结果。请读者观察A×B和B×A的两个结果是否相同，并想想原因。MMULT可以互相循环套用，读者可以自己试着去计算MMULT （MMULT（A，B），MMULT（A，B））。矩阵和其逆矩阵的乘积是单位矩阵，所谓单位矩阵就是对角线是1的方阵。

（7）矩阵的点乘和数乘

请读者进行如下操作，注意观察结果：A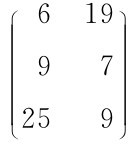＝，在3×2的空白区域内输入＝A×A，按Ctrl＋Shift＋Enter。所谓矩阵的点乘，就是A和B是两个Size完全相同的矩阵。A×B就是将两个矩阵对应位置上的数进行代数意义上的乘法运算，得到的结果矩阵的Size和A及B是一样的。请读者再进行如下操作，注意观察结果：

A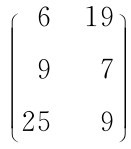＝，在3×2的空白区域内输入＝A×3，按Ctrl＋Shift＋Enter。

所谓矩阵的数乘，就是将矩阵的每一个位置的数都乘以同一个数。

（1）在Excel中，类似于“A．A”，“A×A”这样的矩阵运算都是不合法的。

（2） 的结果是一致的。