比例的定义及其应用：求比例未知项和比例尺的放缩

【知识网络】

【知识梳理】

1.比的意义和性质

（1）比的意义：两个数相除又叫作两个数的比。

3：2读作三比二

“：”是比号，读作“比”。比号前面的数叫作比的前项，比号后面的数叫作比的后项。比的前项除以比的后项所得的商，叫作比值。比值通常用分数表示，也可以用小数或整数表示。

（2）比、除法和分数之间的关系

用字母表示比、除法和分数之间的关系是（b不等于0）。

比和除法、分数相比，比的前项相当于除法中的被除数和分数中的分子，比的后项相当于除法中的除数和分数中的分母，比值相当于除法中的商和分数中的分数值。比的后项、除法中的除数和分数中的分母都不能为0。

（3）比的基本性质

比的前项和比的后项同时乘或除以相同的数（0除外），比值不变，这叫作比的基本性质。

（4）求比值和化简比

求比值的方法：用比的前项除以比的后项，它的结果是一个数，可以是整数，也可以是小数或分数。

化简比的方法：根据比的基本性质可以把比化成最简单的整数比，它的结果必须是一个最简比，即比的前项与后项只有公因数1，也可以用求比值的方法来化简。

求比值和化简比的区别：求比值的最后结果是一个数，化简比的最后结果是一个最简单的整数比。

2.比例的意义和性质

（1）比例的意义：表示两个比相等的式子叫作比例。

组成比例的四个数，叫作比例的项。两端的两项叫作比例的外项，中间的两项叫作比例的内项。比例也可写成分数形式，如a：b=c：d可以写成（b，d均不为0）。

（2）比例的基本性质：在比例里，两个外项的积等于两个内项的积。

（3）判断两个比是否能组成比例的方法：可以看这两个比的比值是否相等，也可以用比例的基本性质来判断。

（4）解比例

根据比例的基本性质，如果已知比例中的任何三项，就可以求出这个比例中的另外一个未知项。求比例中的未知项，叫作解比例。

3.比和比例的区别

4.正比例和反比例

（1）正比例

两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值一定，这两种量就叫作成正比例的量，它们的关系叫作正比例关系。用含有字母的式子表示：。用图象表示是一条过原点（0，0）的直线，这条直线上所有点所对应的两个量的比值相等。

（2）反比例

两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的乘积一定，这两种量就叫作成反比例的量，它们的关系叫作反比例关系。用含有字母的式子表示：xy=k（一定）。

（3）判断正、反比例的方法

一找：找变量。分析数量关系，确定哪两种量是相关联的量。

二看：看定量。分析这两种相关联的量，看它们对应的两个数是比值一定还是乘积一定。

三判断：如果比值一定，那么这两种相关联的量就成正比例关系；如果乘积一定，那么这两种相关联的量就成反比例关系；如果比值和乘积都不是定量，也就不成比例关系。

5.比例尺

（1）意义：一幅图的图上距离和实际距离的比，叫作这幅图的比例尺。

图上距离：=比例尺。

为了计算方便，一般把比例尺写成前项或后项是1的形式。

（2）分类：比例尺按表示形式分，有数值比例尺和线段比例尺。比例尺按放缩程度分，有放大比例尺和缩小比例尺。

（3）应用：

方法一：解比例。

方法二：应用三者之间的数量关系直接列式。

计算：实际距离=图上距离÷比例尺；

图上距离=实际距离×比例尺。

6.问题解决

（1）按比例分配

方法一：先求出一份是多少，再根据各部分所占份数求出相应结果。

方法二：先求出各部分占总数的几分之几，再求出总数的几分之几是多少。

（2）用正、反比例解决问题

a.判断两种相关联的量是否成比例，成什么比例。

b.若这两种相关联的量成正比例，则按“等比”找等量关系；若这两种相关联的量成反比例，则按“等积”找等量关系。

c.设未知数为x，再代入等量关系式中，列出正比例式或反比例式。

d.解比例。

e.检验并写出答语。

（3）图形的放大与缩小：将简单图形按一定比例放大或缩小，图形只是大小发生了变化，形状不变。

注意：图形按n：1（n＞1）放大后，边长、周长扩大到原来的n倍，面积扩大到原来的n2倍。

【指点迷津】

1.把4500g：0.5kg化成最简单的整数比是（　　），比值是（　　）。

【典型错误】　本题容易忽视单位，而直接进行化简。

【分析】　本题中比的前项和比的后项都有单位，而且单位不同，所以先需要统一单位，再进行化简。

【解答】　4500g：0.5kg=4500g：500g=9：1，比值是9。

或者4500g：0.5kg=4.5kg：0.5kg=9：1，比值是9。

因此化成最简单的整数比是9：1，比值是9。

2.两个圆的周长比是4：3，这两个圆的面积之比是（　　）。

【典型错误】　本题容易将两个圆的周长之比认为是它们的面积之比，不推理而直接猜测。

【解答】　圆的周长和它的半径成正比例关系。当两个圆的周长之比是4：3时，它们的半径之比也是4：3。面积之比则是半径的平方之比，即16：9。

3.如果a×b=c×d（a，b，c，d均不为0），那么可以写出哪些比例？

【典型错误】　写比例的时候不分内项和外项，写出a：c=b：d。

【分析】　根据比例的基本性质进行解答。

【解答】　共有八个，分别是

a：c=d：b；a：d=c：b；b：c=d：a；b：d=c：a；

c：a=b：d；c：b=a：d；d：a=b：c；d：b=a：c。

4.在一个比例中，内项分别是9和4，两个比的比值都是2，这个比例是（　　）或（　　）。

【典型错误】　遗漏其中一个比例。

【解答】　根据题意，首先写出比值是2的所有比，分别是18：9，4：2，8：4和9：4.5，再按要求组成比例18：9=4：2；8：4=9：4.5。

5.判断：（1）一本书，已经看的页数和剩下的页数成正比例关系。（　　）

【典型错误】　没有注意定量是比值或积。

【解答】　一本书，已经看的页数和剩下的页数是两个相关联的量，这两个相关联的量的和一定，不是积一定也不是比值一定，所以不成比例。故答案为×。

（2）圆的半径和面积不成比例。（　　）

【典型错误】　没有注意到圆面积和半径的平方的比值才是圆周率。

【解答】　虽然圆的半径和面积是两个相关联的量，但它们的积和比值都不一定，所以不成比例。故答案为×。

6.解比例：。

【典型错误】　本题容易把内项4看作外项，用内项0.6去乘外项3。

【分析】　在本题中，解比例时可以把比例左边部分看成分数形式，然后用对角交叉相乘的方法解决，也可以把比例右边部分看成比的一般形式进行解答。

7.在比例尺是1：2000000的地图上，量得A，B两地间的距离为3.6厘米。如果小李的爸爸开车以每小时60千米的速度行驶，上午8时他从A地出发，那么他到达B地是什么时候？

【典型错误】　比例尺抄错导致计算错误。

【分析】　根据已知信息先求出A，B两地的实际距离，再根据“路程÷速度=时间”求出小李的爸爸需要行驶的时间，最后计算到达的时刻。

【解答】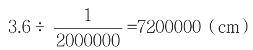　

7200000cm=72km

72÷60=1.2（时）　　1.2时=1时12分

8时+1时12分=9时12分

答：他到达B地是上午9时12分。

8.学校教室改建，用边长是0.5米的方砖铺教室的地面，发现每个教室需要180块。若改用边长是0.6米的方砖，则每个教室需要多少块？

【典型错误】　本题容易把方砖的边长当作面积计算。

【分析】　当铺地面积一定时，每块方砖的面积和相应所需要的方砖块数成反比例，而不是边长和所需要的方砖块数成反比例。

【解答】　设每个教室需要x块方砖。

0.6×0.6×x=0.5×0.5×180

0.36x=45

x=125

答：每个教室需要125块方砖。

【锦囊妙计】

【例1】　甲、乙两数的比是5：6，乙、丙两数的比是3：5，已知甲、乙两数的和是77，则乙、丙两数的和是多少？

【分析】　思路一：按比例分配。(www.xing528.com)

先根据甲、乙两数的比和甲、乙两数的和，求出乙数的大小。再根据乙、丙两数的比以及乙数的大小，求出乙、丙两数的和。

思路二：用三个数的比解决问题。

根据甲、乙两数的比和乙、丙两数的比，转化成甲、乙、丙三个数的连比。根据甲、乙两数的和和对应的份数，求出一份是多少，再根据乙、丙的份数和，求出乙、丙两数的和。

【点拨】　注意在写三个数的连比时，要把其中乙数所占的份数变得相同。

【例2】　2，6，8，24这四个数能否组成比例？

【分析】　思路一：根据比例的意义来判断。判断时要看其中两个数的比值是否等于另两个数的比值；如果相等，则组成比例，否则就不能。

思路二：根据比例的基本性质来判断。判断时要看其中两个数的积是否等于另外两个数的积；如果相等，则组成比例，否则就不能。

【点拨】　判断四个数能否组成比例，可以利用比例的意义来判断，也可以根据比例的基本性质来判断。用比例的基本性质判断时，可以先把最大的数与最小的数相乘，再把剩余的两个数相乘，如果这两个积相等，那么这四个数就能组成比例。

【举一反三】　小方9分钟步行450米，小李1小时走了3千米。小方说：“我们俩各自所行路程和时间的比能组成比例。”小李说：“不能组成比例。”谁说得对？为什么？

【点拨】　解决此类问题时，需要先统一单位。

【例3】　甲和乙两家商城新购进电脑的台数之比是4：3，甲商城卖出24台后，甲和乙两家商城剩余的电脑台数之比为1：3。那么这两家商城分别购进了多少台电脑？

【分析】　思路一：用比例解决。

由题意可知，甲和乙两家商城新购进电脑的台数之比是4：3，如果设甲商城新购进的电脑台数为4x台，那么乙商城新购进的电脑台数为3x台。甲商城卖出24台后，两家商城剩余的电脑台数比为1：3，所以（4x-24）：3x=1：3，通过解比例可求出x的值，进一步可知两家商城分别购进了多少台电脑。

思路二：采用份数法解决问题。

因为乙商城的电脑台数不变，我们把乙商城购进的电脑台数看作3份，则原来甲商城购进电脑台数为4份，卖出后还剩下1份，则卖出了（4-1）份，正好是24台。从而进一步求出一份的台数，继而求出两家商城分别购进的电脑台数。

【点拨】　列比例解决问题时，我们可以借鉴列方程解决问题的方法，先将相等的比用等号连接，列出比例后再解比例。

【举一反三】　学校原有篮球、排球一共40个，篮球与排球的个数之比为7：3，后来又买回来一些篮球。这时篮球与两种球总个数之比是4：5，又买回多少个篮球？

【点拨】　厘清4：5表示的是篮球与两种球总个数之比。

【例4】　一只猎狗发现离它10米的地方有一只野兔，马上去追。猎狗的步子大，它跑3步的路程野兔需要跑5步。但是野兔的动作快，猎狗跑4步的时间，野兔可跑6步。猎狗至少要追多少米才能追上野兔？

【分析】　根据题意可知，猎狗的步长：野兔的步长=5：3，猎狗跑的步数：野兔跑的步数=4：6。因为“步长×步数=路程”，所以猎狗跑的路程：野兔跑的路程=（5×4）：（3×6）=20：18。设猎狗至少要追x米才能追上野兔，则有x：（x-10）=20：18，解出x即可。

【点拨】　“若猎狗的速度：野兔的速度=a：b，猎狗用的时间：野兔用的时间=c：d，则猎狗跑的路程：野兔跑的路程=ac：bd。

【例5】　学校举行50米比赛，当甲冲过终点线时，比乙领先10米，比丙领先20米。如果乙和丙按各自原来的速度继续冲向终点，那么当乙到达终点时，将比丙领先多少米？

【分析】　甲、乙、丙各自的速度一定，在相同时间内，三个人所跑的路程比也一定。甲到达终点时，乙和丙所跑的路程比是（50-10）：（50-20）=4：3；乙到达终点时，乙和丙所跑的路程比还是4：3。

【点拨】　解决这一类问题，先找不变量，再根据不变量确定比例关系，最后列比例解答。

【举一反三】　一根木料，锯成3段需要15分钟，照这样计算，锯成7段需要多少分钟？

【点拨】　锯木头类似于植树，属于“两端不植树”，所以锯成3段需要锯2次。不变量是每锯一次的时间。

【专项训练】

比和比例专项训练A组

一、填空题。

1.在一个比例中，如果甲数的等于乙数的，那么甲数和乙数的比是（　　）。

2.体育馆内人造滑冰场是一个长60米，宽30米的长方形，把它画在比例尺为1：1000的图纸上，图纸上滑冰场的长是（　　）厘米，宽是（　　）厘米。

3.一个三角形的底是30厘米，高是20厘米，把它按1：2缩小后，底是（　　）厘米，高是（　　）厘米，缩小后该三角形的面积是（　　）平方厘米。

4.一段路程，甲小时走完，乙小时走完，甲、乙两人速度的最简整数比为（　　）。

5.1：0.25的比值是（　　）；如果后项乘4，要使比值不变，前项应该变成（　　）；如果前、后项都除以0.25，比值是（　　）。

二、判断题。

1.5：0.8和可以组成比例。　　（　　）

2.在比例里，两个外项互为倒数，其中一个内项是，求另一个内项就是求已知内项的倒数。　　（　　）

3.把10克糖溶解到90克水中，糖与水的质量比是1：10。　　（　　）

4.圆锥的体积一定，底面积和高成正比例。　　（　　）

5.如果x=81y，那么x和y成反比例关系。　　（　　）

三、选择题。

1.下列（　　）组的两个比能组成比例。

A.9：12和12：18　　B.1：5和0.2：2　　C.4：5和0.4：0.5　　D.

2.把4：13的前项加上12，要使比值不变，后项应该（　　）。

A.加12　　B.乘3　　C.乘5　　D.加39

3.等腰直角三角形三个内角的度数比是（　　）。

A.2：2：3　　B.3：2：1　　C.1：2：2　　D.2：1：1

4.把600毫升牛奶倒入不同的圆柱体容器中，容器中牛奶的高度与容器的底面积（　　）。

A.成正比例　　B.成反比例　　C.不成比例　　D.无法判断

5.学校校园长240米，宽180米。而校园的平面图纸的长只有3分米，宽只有2分米，那么选择比例尺（　　）比较合适。

A.1：100　　B.1：1000　　C.1：150　　D.1：1500

四、解比例。

五、解决问题。

1.甲、乙两城相距240千米，一辆小汽车和一辆货车同时从两城相向而行，经过2小时两车相遇。已知两车的速度比是11：9，小汽车和货车的速度各是多少？

2.棉纺厂要给贫困山区捐冬棉服。原计划每天加工300件，15天完成任务。由于天气原因，实际每天比原计划多加工20%。实际多少天完成任务？

3.一个平行四边形被两条线段分割成四个小平行四边形。其中甲、乙、丙的面积分别是20平方米、24平方米、15平方米，那么丁的面积是多少平方米？

4.一辆汽车的行驶路程和耗油量关系如下表所示。

如果这辆汽车出发时油表上显示有油60升，到达某地时油表上显示有油40升，这时它行驶了多少千米？

比和比例专项训练B组

一、填空题。

1.0.1km：300m化成最简整数比是（　　），这个比的比值是（　　）。

2.一项工作，如果甲单独做5天可以完成此项工作的，乙单独做需要12天完成。乙的工作效率与甲的工作效率的最简整数比是（　　）。

3.哥哥和弟弟周末分别骑车去公园锻炼，如图表示他们骑车的路程和时间的关系，请据此填空。

（1）哥哥骑车行驶的路程和时间成（　　）比例。

（2）弟弟骑车每小时行（　　）千米。

（3）哥哥比弟弟早（　　）分钟到达目的地。

二、判断题。

1.比例的两个外项的积与两个内项的积相除，商一定是1。　　（　　）

2.n（n≠0）和它的倒数成正比例关系。　　（　　）

3.某建筑工地修建一条铁路线，已修的长度和未修的长度成反比例关系。　　（　　）

三、选择题。

1.最小的质数和它的倒数的比是（　　）。

A.1：4　　B.4：1　　C.4　　D.2：2

2.若一根木料锯成4段需要9分钟，锯成8段需要x分钟。下列列式正确的是（　　）。

3.墩墩有60枚邮票，雪融有52枚邮票。雪融给墩墩（　　）枚邮票后，墩墩与雪融拥有的邮票数量的比是9：5。

A.40　　B.20　　C.12　　D.24

四、解比例。

1.与x的比等于和3的比，x等于多少？

2.9：3=36：12，如果第三项减去12，那么第一项应减去多少？

五、解决问题。

1.布娃娃“冰墩墩”和“欢欢”的价格之比为7：4，若它们的价格分别上涨35元，价格之比就变成8：5。布娃娃“冰墩墩”的原价是多少元？

2.宇宙飞船飞行轨道的近地点高度为200千米，远地点高度比近地点高度高。宇宙飞船飞行轨道的远地点高度是多少千米？

3.如图，几个罐头盖可以摆出12根吸管的长度？

4.小丁爸爸和小明爸爸是好朋友，他们合伙开了一家美食店。店面房产属小丁爸爸所有，价值30万元，两人各拿出20万元现金投资，年底共盈利21万元。你认为他们应该怎么样分配这笔钱比较合理？

比和比例专项训练C组

一、填空题。

1.在4，5，20三个数中增加一个能组成比例的数，这个数最小是（　　），这个比例是（　　）。

2.A，B两个货仓共有5.1吨货物，现在从A货仓中取出0.4吨货物放入B货仓，这时A货仓货物质量的40%等于B货仓货物质量的，B货仓原来有货物（　　）吨。

3.在三角形ABC中，D为BC的中点，E为AB上的一点，且。已知四边形BDME的面积是35，那么三角形ABC的面积是（　　）。

二、选择题。

1.丽丽每天为妈妈泡一杯红糖水，下面四天里，红糖水最甜的一天是（　　）。

A.第一天，25克红糖和200毫升水　　B.第二天，红糖和水的比是1：10

C.第三天，30克红糖配成的250克红糖水　　D.第四天，红糖水中红糖含量为13%

2.有A，B两条绳子，第一次剪去A绳的，B绳的；第二次剪去A绳剩下的，B绳剩下的；第三次剪去A绳剩下的，B绳剩下的，最后A绳剩下的长度与B绳剩下的长度比为2：1，则原来两条绳子长度的比是（　　）。

A.10：9　　B.9：10　　C.2：1　　D.1：2

3.三个分数的和是3.375，它们的分母相同时，分子的比为2：3：4，则它们中最小的分数为（　　）。

4.有三堆棋子，每堆棋子一样多，并且每堆都有黑、白两色棋子。第一堆里的黑棋子和第二堆里的白棋子的数量相等，第三堆里的黑棋子数量占全部棋子数量的，把这三堆棋子集中在一起，白棋子数量占全部棋子数量的（　　）。

三、解决问题。

1.某市居民自来水收费标准如下：每户每月用水5吨以下收费2.2元／吨；超过5吨时，超出部分收费3.2元／吨。某月，张、李两户共交72元水费，用水量之比为5：3，张家应付水费多少元？

2.小红爸爸从家里出发骑自行车去森林公园，计划用时为3时20分。由于途中有2.5千米的路面在整修，小红爸爸只能推车步行。小红爸爸步行的速度只有骑自行车速度的，结果小红爸爸用时3时40分才到达森林公园。小红家到森林公园的距离是多少千米？