【知识网络】
【知识梳理】
1.用字母表示数
（1）用含有字母的式子表示数量关系。
例如：爸爸比小红大30岁，小红是a岁，则爸爸是（a+30）岁。
例如：用同样的力，在月球上，人能举起的物体的质量是地球上的6倍。如果x表示人在地球上能举起的物体的质量，那么用同样的力，人在月球上能举起的物体的质量就是6x。
例如：一大杯果汁一共1200克，倒了3小杯，如果每小杯是x克，则这一大杯果汁还剩（1200-3x）克。
例如：摆一个三角形要用3根小棒，摆一个正方形要用4根小棒，摆了x个三角形和x个正方形，一共要用（3x+4x）根小棒。
（2）用含有字母的式子表示运算定律。
例如：加法交换律可以用字母表示为a+b=b+a。
（3）用含有字母的式子表示几何图形的周长、面积和体积的计算公式。
例如：边长为a的正方形的周长公式可以表示为C=4a。
2.求代数式的值
当字母的数值确定时，把它代入原式中进行计算，所得的结果就是含字母的式子的值。
3.方程的意义
含有未知数的等式叫作方程。
例如：3x+2.5=30.6是方程，而3x+25不是方程，5x+36＞100也不是方程。
4.等式的性质
等式的性质1：等式两边加上或减去同一个数，等式两边仍然相等。
等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，等式两边仍然相等。
5.解方程
方程的解：使方程左右两边相等的未知数的值，叫作方程的解。
例如：x=3是方程8x=24的解。
解方程：求方程的解的过程叫作解方程。
【指点迷津】
1.一个两位数，十位上的数字是a，个位上的数字是b，这个两位数用含字母的式子表示是（ ）。
【典型错误】 a+b
【分析】 出错原因是不清楚每个数位上的数字表示什么。
【解答】 10a+b
【点拨】 用字母表示多位数时，每个数位上的数字都要乘其数位对应的计数单位，再相加。
【跟踪练习】 一个三位数，百位上的数字是a，十位上的数字是b，个位上的数字是c，这个三位数用含字母的式子表示是（ ）。
2.鞋的尺码和鞋底的长度之间的关系可以用y=2x-10（y表示尺码数，x表示厘米数）来表示。小红买了37码的鞋，该鞋的鞋底长（ ）厘米。
【典型错误】 13.5
【分析】 出错原因是把字母表示的数值代入算式时计算出错。
【解答】 已知尺码数是37，所以代入公式可得：37=2x-10
2x=37+10
2x=47
x=23.5
【点拨】 解决此类题时只要把字母表示的数值代入算式计算即可。
【跟踪练习】 （1）已知x=1，y=2，z=3，则4x+y-z=（ ）。
（2）已知2x+1=5，则4x+2=（ ）。
3.解方程：
。
【典型错误】 
【分析】 出错原因是没有很好地掌握利用等式的性质解方程。
【点拨】 本题考查的是利用等式的性质解方程。
【跟踪练习】 解方程。
【锦囊妙计】
1.用字母表示数
【例1】 在一个边长为a的正方形纸上剪下一个最大的圆，该圆的面积是多少？剩下部分的面积是多少？
【分析】 此题考查的是用字母表示数和正方形、圆的面积的计算公式的应用。在一个边长为a的正方形纸上剪下一个最大的圆，则圆的直径就是正方形的边长，要求剩下部分的面积，用正方形的面积减去圆的面积即可。
【解答】 圆的面积是
；剩下部分的面积是
。
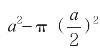【举一反三】 例1中得到的圆的周长是多少？剩下部分的周长是多少？
2.求含有字母的式子的值
【例2】 一本书有x页，丽丽每天看10页，看了y天还没看完。
（1）用含有字母的式子来表示未看的页数。
（2）当x=120，y=9时，利用上面的式子，求未看的页数。
【分析】 此题考查的等量关系是“未看的页数=总页数-已看的页数”，已知总页数是x页，已经看了10y页，因此未看的页数是x-10y。把x=120，y=9代入含有字母的式子中计算，就可求出未看的页数。
【解答】 （1）x-10y
（2）当x=120，y=9时，x-10y=120-10×9=30（页）。
【例3】 已知m-2n=5，求3m-6n+4的值。
【分析】 本题综合性强，解法灵活，在m-2n=5中有两个未知数，无法求出m，n分别是多少，这里要比较两个式子中含有未知数的部分，可发现两者刚好是3倍关系。
【解答】 方法一：
当m-2n=5时，
3m-6n+4
=3（m-2n）+4
=3×5+4
=19
方法二：
因为m-2n=5，所以3m-6n=15，
3m-6n+4
=15+4
=19
方法三：
因为m-2n=5，所以m=5+2n，
当m=5+2n时，
3m-6n+4
=3（5+2n）-6n+4
=15+6n-6n+4
=15+4
=19
【举一反三】 （1）某超市推出购物酬宾活动：凡一次性购物满88元按七折优惠。小明在该超市买了单价为50元的学习用品n件（n＞2），用含有字母n的式子表示应付款数。当n=5时，应付款多少元？
（2）当
时，求
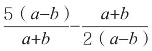的值。
3.解方程
【例4】 列方程解文字题。
x的
与48的25%相等，x是多少？
【举一反三】 （1）x的3倍加上1.5与1.2的积，和是16.8，x是多少？
（2）已知两个数的和是22.7，差是8.9，求这两个数分别是多少。(www.xing528.com)
4.列方程解决实际问题
【例5】 地球的表面积为5.1亿平方千米，其中海洋面积约为陆地面积的2.4倍。地球上的海洋面积和陆地面积分别是多少亿平方千米？
【分析】 海洋面积和陆地面积都是未知的，怎样设呢？等量关系又是什么呢？
方法一：设陆地面积是x亿平方千米，则海洋面积为2.4x亿平方千米。根据等量关系“海洋面积+陆地面积=地球表面积”列方程，得2.4x+x=5.1。
方法二：设陆地面积是x亿平方千米，则海洋面积为（5.1-x）亿平方千米。根据等量关系“陆地面积×2.4=海洋面积”列方程，得2.4x=5.1-x。
【解答】 方法一：
2.4x+x=5.1
3.4x=5.1
x=1.5
2.4x=2.4×1.5=3.6
方法二：
2.4x=5.1-x
3.4x=5.1
x=1.5
5.1-x=5.1-1.5=3.6
答：地球上的海洋面积是3.6亿平方千米，陆地面积是1.5亿平方千米。
【举一反三】 （1）一头东北虎的体重为280千克，比一只羊的体重的7倍少7千克，这只羊重多少千克？
（2）妈妈今年的年龄是小明的3倍，且两人年龄之和是44岁，小明和妈妈今年分别是多少岁？
【专项训练】
简易方程专项训练A组
一、填空题。
1.练习本每本a元，嘉嘉买了3本，付了b元，可以找回（ ）元。
2.李叔叔每小时完成m个零件，3小时能完成（ ）个零件，t小时能完成（ ）个零件。
3.妈妈买了15千克水果，花了x元，x÷15表示（ ）。
4.等腰三角形的一个底角是a°，用含字母的式子表示它的顶角是（ ）°，；当a=30时，顶角是（ ）°。
5.在
里填上适当的数，使每个方程的解都是x=9。
二、判断题。
1.方程一定是等式，等式不一定是方程。 （ ）
2.解方程2x-3.5=6.9时，方程两边要先同时减去3.5。 （ ）
3.规定a＊b=2a-3b，则5＊2=2×5-3×2。 （ ）
4.两个连续自然数的和是x，那么较大的自然数是：x÷2+1。 （ ）
三、选择题。
1.下列各式中，（ ）是方程。
A.5+3=8 B.5=3x-1 C.4+x＞7 D.8x+32
2.y=1.4是方程（ ）的解。
A.y+3.5=4.8 B.y÷1.2=4.5 C.4y=5.6 D.y-4.2=0.8
3.李师傅每小时做x个零件，王师傅每小时做y个零件，5（x-y）表示（ ）。
A.两人5小时共做零件的个数
B.李师傅比王师傅每小时多做的个数
C.共做5小时，两人相差的个数
4.解方程（56-2x）÷4=2.5时，先把（ ）看作一个整体，再把（ ）看作一个整体。
A.56-2x B.（56-2x）÷4 C.2x
5.甲有x支笔，乙有y支笔，甲给乙5支笔后两人的笔同样多，下列关系正确的是（ ）。
A.x-5=y B.x=y+5 C.x-5=y+5 D.x+10=y
四、解方程。
五、列方程求解。
1.一个数的50%比它的
多5，这个数是多少？
2.一个数与28的差的2.5倍是10，求这个数。
六、看图列方程并解答。
七、列方程解决问题。
1.一批零件共300个，师徒两人用了5小时完成，师傅平均每小时做45个，徒弟平均每小时做几个？
2.张伯伯养了60只鸡，其中母鸡数量是公鸡的3倍，张伯伯养了母鸡和公鸡各多少只？
简易方程专项训练B组
一、填空题。
1.9＊2=9+8，5＊4=5+4+3+2，那么x＊3=6时，x=（ ）。
2.小圆的半径是a，大圆的半径等于小圆的周长，大圆的周长是（ ）。
3.圆柱体的底面半径为r，高为h。如果半径不变，高增加3，则圆柱体的体积增加（ ），表面积增加（ ）。
4.华氏度=摄氏度×1.8+32，某天的最高气温是86华氏度，相当于（ ）摄氏度。
5.x是正整数。若2x+1=11，则x=（ ）；若2x+1＜11，则x可以是（ ）；若2x+1＞11，则x可以是（ ）。
二、选择题。
1.m是大于0的数，（m+m+m）÷m+（m-m）×m的结果是（ ）。
A.m B.3 C.3+m D.1
2.小红今年m岁，爸爸今年（m+28）岁，5年后他们的年龄之和是（ ）岁。
A.28 B.2m+28 C.2m+38
3.有这样一组数：0，2，4，6，8，10， …，那么第n个数是（ ）。
A.2n+1 B.2n-1
C.2n D.2n-2
4.多多比妈妈矮m厘米，爸爸比多多高n厘米，已知n＞m，则爸爸比妈妈（ ）。
A.高（n-m）厘米 B.矮（n-m）厘米
C.高（n+m）厘米 D.无法判断
5.下列（ ）图的阴影部分的面积可以用
来表示。
三、先画线段图，再列出方程，不计算。
1.琳琳有一些零花钱，她先用了总数的
，再用了总数的25%，又拿出110元买了一套图书，这些零花钱刚好用完。琳琳原来有多少零花钱？
2.学校有男生450人，比女生少
，学校有女生多少人？
四、列方程解决问题。
1.五（3）班去野营，班长说：“一个人一个饭碗，两个人一个菜碗，三个人一个汤碗，我们需要带55个碗。”五（3）班共有多少人？
2.妹妹比姐姐多56块钱，妹妹每天花掉6块钱，姐姐每天做家务赚8块钱，几天后两人的钱同样多？
简易方程专项训练C组
1.用含字母的式子表示下列图形中涂色部分的面积。
2.如图，按规律摆放小棒：
（1）像这样摆下去，摆n层，共需要（ ）根小棒。
（2）当n=5时，需要的小棒数是多少？
3.甲、乙两队合修一段长1500米的路，两队同时开工，5天修完。已知甲队每天修120米，乙队每天修多少米？设乙队每天修x米，你能列出几个不同的方程？试一试。（想到几种写几种，只列方程不计算）
4.高速公路上发生车祸（该路段限速120千米/时），当警方达到车祸现场时，肇事司机告诉警察，他在车祸前以130千米/时的速度在路面上行驶，警方测量出这辆汽车留下的刹车痕迹为60米，请问该车主是否撒谎？请说明理由。
[估算一辆汽车在刹车前一刻的速度，会采用公式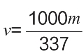
，v（千米/时）表示汽车在刹车前一刻至少有的速度，m（米）表示刹车痕迹的长度]
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
