四则运算的概念及运算顺序详解：加法、减法、乘法、除法的正确使用方法

【知识网络】

【知识梳理】

（一）四则运算的概念和运算顺序

1.加法、减法、乘法和除法统称四则运算。

2.在没有括号的算式里，如果只有加、减法或者只有乘、除法，都要从左往右按顺序计算。

3.在没有括号的算式里，既有乘、除法又有加、减法，要先算乘、除法，再算加、减法。

4.算式有括号，要先算括号里面的，再算括号外面的；大、中、小括号的计算顺序为小→中→大。括号里面的计算顺序遵循以上1、2、3条的计算顺序。

（二）0的运算

1.0不能做除数，a÷0是错误的表达。

2.一个数加上0得原数。字母表示：a+0=a。

3.一个数减去0得原数。字母表示：a-0=a。

4.一个数减去本身，差是0。字母表示：a-a=0。

5.一个数和0相乘，得0。字母表示：a×0=0。

6.0除以任何非0的数，得0。字母表示：0÷a=0（a≠0）。

（三）运算定律

1.加法交换律

在两个数的加法运算中，交换两个加数的位置，和不变。字母表示：a+b=b+a。

2.加法结合律

三个数相加，先把前两个数相加，再加另一个数，或者先把后两个数相加，再加另一个数，和不变。字母表示：（a+b）+c=a+（b+c）。

3.乘法交换律

在两个数相乘的乘法运算中，交换两个乘数的位置，积不变。字母表示：a×b=b×a。

4.乘法结合律

三个数相乘，先把前两个数相乘，再乘另一个数，或先把后两个数相乘，再乘另一个数，积不变。字母表示：（a×b）×c=a×（b×c）。

5.乘法分配律

两个数相加（或相减）再乘另一个数，可以先把它们分别与这个数相乘，再把两个积相加（或相减），得数不变。字母表示：

（1）（a+b）×c=a×c+b×c；a×c+b×c=（a+b）×c。

（2）a×（b-c）=a×b-a×c；a×b-a×c=a×（b-c）。

6.连减定律

（1）一个数连续减两个数，等于这个数减这两个数的和，得数不变。字母表示：

a-b-c=a-（b+c）；a-（b+c）=a-b-c。

（2）在三个数的加、减法运算中，交换后两个数（带加、减号）的位置，得数不变。字母表示：a-b-c=a-c-b；a-b+c=a+c-b。

7.连除定律

（1）一个数连续除以两个数，等于这个数除以这两个数的积，得数不变。字母表示：

a÷b÷c=a÷（b×c）；a÷（b×c）=a÷b÷c。

（2）在三个数的乘、除法运算中，交换后两个数（带乘、除号）的位置，得数不变。字母表示：a÷b÷c=a÷c÷b；a÷b×c=a×c÷b。

【指点迷津】

1.计算。

【典型错误】　原式=1÷1

=1

【分析】　因为除号两边都是“”，很容易将题目看成，从而使原题的运算顺序发生改变。这道题目里只有乘、除法，运算的顺序应该是从左往右，或者简便运算，先算。

2.计算：。

【分析】　这道题很容易会先计算“”，这样计算看似简单，但改变了运算顺序，从而导致计算结果错误。遇到题目里只有乘、除法，我们不能改变运算顺序，应该从左往右计算，将“”转换成“×3”后再计算。

3.计算：3.2×2.5×125。

【典型错误】　原式=（0.4×8）×2.5×125

=（0.4×2.5）+（8×125）

=1+1000

=1001

【分析】　计算时，当看到因数“25”，我们就会想到“4”，当看到因数“125”，我们就会想到“8”，这道题中的因数“3.2”中就隐藏着“4”和“8”，将3.2拆分后题目变成了“（0.4×8）×2.5×125”。但之后的计算很容易错用乘法分配律，乘法分配律用字母表示是“（a+b）×c=ac+bc”，而题目中是连乘，我们应该用乘法交换律和乘法结合律进行简便运算。

【解答】　3.2×2.5×125

=（0.4×8）×2.5×125

=（0.4×2.5）×（8×125）

=1×1000

=1000

4.计算：。

【分析】　这道题目我们可以用乘法分配律进行简便计算，我们知道乘法分配律用字母表示是“（a+b）×c=ac+bc”，而这道题目中的“c”并非是5，也不是9，而是“5×9”，所以我们在这里要将“5×9”看作一个整体，同时分配给和，为了使后面的计算更加简便，建议不要先把“5×9”计算出来。

5.计算：。

【典型错误】

【分析】　通过观察，我们发现可以通过改变运算顺序使这道题的计算更加简便，改变运算顺序前我们首先要去括号。在加、减法运算中，如果括号前面是减号，去掉括号时我们要改变括号内的运算符号，而不能直接将括号去掉，正确的运算方法如下。

6.计算：。

【分析】　遇到这种题型，很多同学容易掉入陷阱，运用“除法分配律”来计算，但实际运算中“除法分配律”并不成立。遇到这样的题目，没有简便方法，只能根据一般的计算方法，先算括号内的，再算括号外的。

【锦囊妙计】

（一）综合算式。1.根据分步列式写出综合算式

【例1】　分步列式：34÷2=17　　24×10=240　　17+240=257

综合列式：__________________________

【分析】　代入法：最后一个等式中的17用算式34÷2代入，240用24×10代入，然后观察运算顺序是否合适，如果分步中先算的加、减法，列成综合算式后要添上括号。

【解答】　34÷2+24×10=257

2.根据文字描述写出综合算式

【例2】　文字描述：34除以2的商与24乘10的积相加，和是多少？

综合列式：__________________________

【分析】　此题可以用下列两种方法分析。

第一种（顺向思维）：“34除以2的商与24乘10的积相加，和是多少？”根据34除以2的商列出算式34÷2，根据24乘10的积列出算式24×10，再把两道算式看成两个数进行相加求和。

第二种（逆向思维）：

第一步：根据最后求“和是多少”想加法留白算式________+________。

第二步：根据先求商和积，将算式34÷2和24×10填入第一步加法留白算式中形成综合算式。

【解答】　34÷2+24×10

【注意】　（1）仔细审题。特别要注意“除以”和“除”的不同含义。

（2）厘清运算顺序。特别要注意先算乘、除法还是加、减法，别忘了添上括号。

（3）列式计算别忘验算。

（二）简便运算

1.巧借（有借有还，再借不难）

【例1】　（1）9999+999+99+9

=10000+1000+100+10-1-1-1-1（借1还1）

=11110-4

=11106

（2）4821-998

=4821-1000+2（借2还2）

=3821+2

=3823

【注意】　第（1）题是多加了要减，第（2）题是多减了要加。

2.关注构造，巧找相同因数（让我们的算式满足乘法分配律的条件）

【例2】　（1）3.8×9.9+0.38

=3.8×9.9+3.8×0.1（把0.38转化成3.8×0.1）(www.xing528.com)

=3.8×（9.9+0.1）

=3.8×10

=38

（3）

（关注不同形式的数和乘、除法的转化）

=1.5×（7.4+0.6+2）

=1.5×10

=15

3.分拆（不要改变数的大小）

【例3】　（1）1.25×88

=1.25×8×11

=10×11

=110

（2）1.25×88

=1.25×（8+80）

=1.25×8+1.25×80

=10+100

=110

【注意】　第（3）题中，但如果是类似于的分数，需要分拆成。

分拆时，分数大小不变！

【专项训练】

四则运算专项训练A组

一、填空题。

1.二成五=（　　）：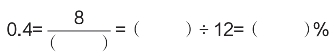

2.把3米长的铁丝平均截成4段，每段占全长的，每段是1米的。

3.（1）6.05千米=（　　）千米（　　）米　　（2）2吨15千克=（　　）吨　　（3）85分=（　　）时

4.比（　　）米多25%是3.5米。60吨比（　　）吨少25%。

5.把一根长为1米的方木料，锯成相等的4段，表面积比原来增加了30平方厘米，原木料的体积是（　　）。

6.（　　）的是27；48的是（　　）。

7.小明把8×（▲-3）错看成8×▲-3，他得到的答案与正确答案相差（　　）。

8.已知那么将a，b，c从小到大排列是（　　）。

9.有48.75吨货物，每次运走它的，那么（　　）次可以运完。

10.在里填上“＞”“＜”或“=”。

二、判断题。

1.4米长的钢管，剪下米后，还剩下3米。　　（　　）

2.20千克减少后再增加，结果还是20千克。　　（　　）

3.松树的棵数比柏树多，柏树的棵数就比松树少。　　（　　）

4.两个真分数的积一定小于1。　　（　　）

5.一桶油用去它的，则剩下的油比用去的油多。　　（　　）

三、计算题。

1.直接写出得数。

2.脱式计算（怎样简便怎样计算）。

3.列式计算。

（1）一个数的，这个数是多少？　　（2）减去 的积，所得的差除以9，商是几？

四、计算下列物体的表面积。

五、解决问题。

1.四（1）班学生在学校运动会上得了40分，比四（2）班学生得分的2倍少24分，四（2）班学生得了多少分？

2.一件上衣90元，是裤子价钱的，买这样的一套衣服需要多少元？

3.买一辆汽车，如果分期付款要加价7%，而一次性付款则可享受“九五折”优惠。李叔叔算了一下，发现分期付款要比一次性购买多付7200元，你知道这辆汽车原价是多少元吗？

4.绘画小组原有42人，女生人数占总人数的，加入了若干名女生后，男女生人数比为6：5。现在绘画小组有多少人？

5.从A地去B地，货车需要90分钟，客车需要80分钟。货车每分钟行千米，客车每分钟行多少千米？

6.一个三位数，个位上的数字是3，如果把3放到百位，原来百位上的数字放到十位，原来十位上的数字放到个位，就组成一个新的三位数，新数比原数小171，则原数是多少？

四则运算专项训练B组

一、填空题。

1.，则c=（　　）。

2.如果，那么6▲（4▲8）=（　　）。

3.数a除以数b，商是12，余数是4。如果数a加上3，再除以数b，商是13，余数是0，则数a是（　　）。

4.用1，4，5，6四个数字（每个数字必须用，且只能用一次），通过四则运算（+、-、×、÷和括号），使计算结果为24。写出满足条件的综合算式：_________________________。

二、选择题。

1.如果，那么a是（　　）。

A.真分数　　B.假分数　　C.1　　D.2

2.估算6.18×8.29时，误差最小的算式是（　　）。

A.6×8　　B.6×9　　C.7×8　　D.7×9

3.的范围是（　　）。

A.2017～2018　　B.2018～2019　　C.2019～2020　　D.2020～2021

4.当x和y同时扩大到原来的2倍时，的值（　　）。

A.扩大到原来的2倍　　B.扩大到原来的4倍

C.不变　　D.缩小到原来的

5.已知a，b，c，d都不为零，设n=a÷b×c÷d，那么下列与n不相等的算式是（　　）。

A.a÷b×（c÷d）　　B.a÷（b×c）÷d

C.a×c÷（b×d）　　D.a÷b÷（d÷c）

三、脱式计算（怎样简便怎样计算）。

四、列式计算。

1.0.2与它的倒数的和除以3与的差，商是多少？

2.从35里减去25的，所得的差去除，得数是多少？

四则运算专项训练C组

一、填空题

1.。

2.M⊕N=4M+5N，若x⊕6=46，则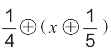的值是（　　）。

3.已知2×2=4，那么，那么，那么，那么；根据你对的理解，计算：。

4.。

5.某练习册共有n页，小红将这些页码全部加起来时，不小心把某一页错加了两次，结果得到1845，则这本书共有（　　）页，错加的那一页是第（　　）页。

6.如果符号[a]表示数a的整数部分，例如，那么根据以上算法，。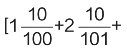

7.3+8+13+18+…+n=（　　）。（结果用n表示）

8.。

9.已知n2=n×n，则12+22+32+…+20182+20192的末位数字是（　　）。

二、计算题。

三、列式计算。

1.如果，根据以上信息，计算。

2.已知a2-b2=（a+b）×（a-b），分数的平方可以写成，根据以上信息，计算 。