求最大公因数和最小公倍数的方法：短除法与互质数的运用

【知识网络】

【知识梳理】

1.整除

被除数、除数和商都是大于零的自然数。

2.因数和倍数

（1）如果a÷b=c（a，b，c都是非0自然数），那么a是b，c的倍数，b，c是a的因数。

（2）因数和倍数这两个不同的概念是相互依存的，不能单独说一个数是因数，或者一个数是倍数，只能说一个数是另一个数的因数，或者一个数是另一个数的倍数。例如：4×3=12，12是4的倍数，12也是3的倍数，4和3都是12的因数。

（3）因数和倍数的特征

一个数的因数的个数是有限的，其中最小的因数是1，最大的因数是本身。

一个数的倍数的个数是无限的，最小的倍数是本身，没有最大的倍数。

（4）一个数最大的因数=这个数最小的倍数=这个数本身。

3.奇数和偶数

（1）概念

奇数：整数中不是2的倍数的数叫奇数。自然数中最小的奇数是1。

偶数：整数中是2的倍数的数叫偶数。自然数中最小的偶数是0。

（2）特征

奇数：个位上是1，3，5，7或9的数。

偶数：个位上是0，2，4，6或8的数。

（3）字母表示

奇数：2n+1（n为整数）。

偶数：2n（n为整数）。

（4）两数之和（积）的奇偶性

奇数+奇数=偶数，奇数+偶数=奇数，偶数+偶数=偶数；奇数×奇数=奇数，奇数×偶数=偶数，偶数×偶数=偶数。

（5）自然数不是奇数就是偶数。

4.倍数特征

（1）2的倍数的特征：个位是0，2，4，6或8。

（2）5的倍数的特征：个位是0或5。

（3）同时是2和5的倍数的特征：个位是0。

（4）3的倍数的特征：各个数位上的数字之和是3的倍数。

（5）9的倍数的特征：各个数位上的数字之和是9的倍数。

（6）能同时被2，3，5整除的最小两位数是30，最大两位数是90；最小三位数是120，最大三位数是990。

5.质数和合数

（1）概念

质数：只有1和它本身两个因数的数（只有2个因数）。

合数：除了1和它本身还有别的因数的数（至少有3个因数）。

（2）最小的质数是2，最小的合数是4。

（3）1既不是质数，也不是合数。（因为1只有1个因数）

（4）自然数中，除了0和1，其余的数不是质数就是合数。

（5）在自然数中，不是奇数的质数只有2。

（6）规律：质数×质数=合数，质数×合数=合数，合数×合数=合数。

（7）100以内的质数：2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97。

6.分解质因数

把一个合数写成几个质数相乘的形式（常用短除法分解质因数）。

7.公因数、最大公因数

（1）几个数公有的因数叫这几个数的公因数。其中最大的那个就叫它们的最大公因数。

（2）两个数的公因数只有1，就说这两个数互质。

（3）用短除法求几个数的最大公因数：除到互质为止，再把所有的除数连乘起来。

（4）两个数互质的特殊情况

1和任何正整数互质；相邻两个正整数互质；两个不同的质数一定互质；2和所有奇数互质；质数与比它小的合数互质。

（5）如果两个数是倍数关系，那么较小的数就是它们的最大公因数。

如果两个数互质，那么1就是它们的最大公因数。

8.公倍数、最小公倍数

（1）几个数公有的倍数叫作这几个数的公倍数。其中最小的那个就叫它们的最小公倍数。

（2）如果两个数是倍数关系，那么较大的数就是它们的最小公倍数。

如果两个数互质，那么它们的乘积就是它们的最小公倍数。

【指点迷津】

1.2×3×6=36，2，3，6这三个数都是36的（　　）。

A.倍数　　B.质因数　　C.公因数　　D.因数

【分析】　因为2×3×6=36，说明2，3，6是36的因数，只有2和3是质数，所以2和3是36的质因数，但6不是质数，是合数，由此选出答案即可。

【解答】　因为2×3×6=36，所以2，3，6是36的因数。故选D。

【点拨】　此题主要考查质因数与因数的区别：一个数的因数可以是质数、合数，也可以是1，而一个数的质因数一定是质数。

2.小明有数量相同的5元和1元纸币若干张，那么小明拥有的总钱数可能是（　　）。

A.38元　　B.36元　　C.26元

【分析】　因为小明有数量相同的5元和1元纸币若干张，可知小明的总钱数是6的倍数，根据选项即可得出答案。

【解答】　设5元有x张，则1元有x张， 5x+1x=6x，小明的总钱数是6的倍数，故选B。

【点拨】　根据找一个数的倍数的方法，在选项中找出6的倍数即可。

3.已知a是自然数，那么2a+1一定是（　　）。

A.奇数　　B.偶数

C.奇数或偶数　　D.既不是奇数也不是偶数

【分析】　自然数是用来表示物体个数的数；奇数不是2的倍数。

【解答】　a是自然数，那么2a+1一定是奇数。故选A。

【点拨】　此题考查的是自然数和奇数的意义。

4.要使三位数36□同时是2，3，5的倍数，□里应填（　　）。

A.0　　B.2　　C.5

【分析】　根据2，3，5的倍数的特征可知该三位数的个位是0，进而得出结论。

【解答】　由分析可知，□里应填0。故选A。

【点拨】　此题根据2，3，5的倍数的特征分析、解答即可。

5.a，b，c是非零自然数，a×b=c，下列说法正确的是（　　）。

A.a是b的最大公因数

B.b是a和c的公因数

C.c是a和b的公倍数

D.c是a和b的最小公倍数

【分析】　根据公倍数的意义：几个数公有的倍数，叫做这几个数的公倍数，进行解答即可。

【解答】　a，b，c是非零自然数，a×b=c，即a和b是c的因数，c是a和b的公倍数。故选C。

【点拨】　此题考查公倍数的意义，应掌握其意义，并能灵活运用。

6.一个数既是3和5的倍数，又是7和10的倍数，那么这个数最小应该是（　　）。

A.105　　B.150　　C.210　　D.350

【分析】　一个数既是3和5的倍数，又是7和10的倍数，那么这个数是3，5，7，10的公倍数，根据题目要求，求出最小公倍数即可。

【解答】　3，5，7，10的最小公倍数是：3×7×10=210。故选C。

【点拨】　有公有质因数的两个数，最小公倍数是这两个数的公有质因数与独有质因数连乘的积。

7.一个数最小的倍数（　　）等于这个数最大的因数。

A.可能　　B.不可能

C.一定　　D.不太可能

【分析】　根据“一个数最大的因数是它本身；一个数最小的倍数是它本身”，进而得出结论，进行判断。

【解答】　C

【点拨】　解答此题应明确一个数最大的因数与一个数最小的倍数之间的关系。

8.在自然数中，最小的奇数、偶数、质数、合数的和是（　　）。

A.7　　B.8　　C.9

【分析】　先确定在自然数中，最小的奇数、偶数、质数、合数分别是几，再计算。

【解答】　在自然数中，最小的奇数是1，最小的偶数是0，最小的质数是2，最小的合数是4，所以和为1+0+2+4=7。故选A。

【点拨】　解决本题的关键是找出在自然数中，最小的奇数、偶数、质数、合数分别是几，再计算。

9.三个连续奇数，如果中间一个用m表示，则前一个是（　　），后一个是（　　）。

A.m+2　　B.m-2　　C.m+l　　D.m-1

【分析】　因为相邻的两个奇数相差2，所以三个连续奇数，前一个比中间一个少2，后一个比中间一个多2，据此解答即可。

【解答】　三个连续奇数，如果中间一个用m表示，则前一个是m-2，后一个是m+2。故选B、A。

【点拨】　解答这类用字母表示数的题目时，解题关键是根据已知条件，把未知的数用字母正确地表示出来，然后根据题意列式计算。

10.a=2×2×3×3，a有（　　）个因数。

A.3　　B.4　　C.9

【分析】　根据找一个数的因数的方法，进行列举。a的因数有：1，2，3，2×2=4，2×3=6， 3×3=9，2×2×3=12，2×3×3=18，2×2×3×3=36。

【解答】　由分析可知，a的因数共有9个。故选C。

【点拨】　解答此题应根据找一个数的因数的方法，进行列举即可。

11.判断：两个数是互质数，这两个数没有公因数。（　　）

【分析】　根据互质数的意义，公因数只有1的两个数叫作互质数，以此判断即可。

【解答】　因为公因数只有1的两个数叫作互质数，所以“两个数是互质数，这两个数没有公因数”的说法是错误的。故答案为×。

【点拨】　此题主要考查互质数的意义以及判断两个数是不是互质数的方法。

12.判断：18是1.8的倍数。（　　）(www.xing528.com)

【分析】　若整数a能够被整数b整除，a叫作b的倍数，b就叫作a的因数，因数与倍数是相互依存的，是指非0自然数，据此判断。

【解答】　因为倍数和因数指的是非0自然数，所以“18是1.8的倍数”的说法是错误的。故答案为×。

【点拨】　本题主要考查因数与倍数的意义，注意因数与倍数是相互依存的，指的是非0自然数。

13.三个连续奇数的和是645。这三个奇数中，最小的奇数是（　　）。

【分析】　用“645÷3=215”求出中间的那个奇数，因为两个连续的奇数相差“2”，所以再减去2就是最小的奇数。

【解答】　645÷3-2=215-2=213，所以这三个奇数中，最小的奇数是213。故答案为213。

【点拨】　此题的关键是求出中间的那个奇数，然后根据两个连续的奇数相差“2”，进行解答。

【锦囊妙计】

1.分解质因数的方法

方法一：对于一个较小的数，可采用塔式图进行分解。

方法二（短除法）：把要分解质因数的数写在短除号“∟”里，在被除数的左边写出除数（除数一定是质数，一般按从小到大的顺序，从最小的质数开始除），如果得到的商还是合数，就按照上面的方法继续除，直到得到的商是质数为止。最后把所有除数和最后得到的商写成连乘的形式。

【例1】　将48分解质因数。

【解答】

2.求最大公因数的方法

（1）枚举法：求几个数的最大公因数，可以将这几个数的因数全部枚举出来，从中找到的公有的因数，就是这几个数的公因数，其中最大的就是这几个数的最大公因数。

（2）分解质因数法：先把几个数分解质因数，再把这几个数全部公有的质因数连乘起来，所得的积就是要求的最大公因数。

（3）短除法：一般先把几个数的公因数作为除数，依次去除这几个数，把除得的商分别写在这几个数的下方，一直除到各个商只有公因数1为止，然后把所有除数连乘起来，所得的积就是这几个数的最大公因数。

【例2】　求18和24的最大公因数。

18和24的公因数有1，2，3，6，所以18和24的最大公因数是6。

（2）分解质因数法：

18=2×3×3，24=2×2×2×3。

18和24都含有质因数2和3，所以它们的最大公因数是2×3=6。

（3）短除法：

18和24的最大公因数是2×3=6。

3.求最小公倍数的方法

（1）枚举法：求几个数的最小公倍数，可以将这几个数的倍数从小到大依次枚举出来，从中找到相同且最小的。

（2）分解质因数法：求两个数的最小公倍数，先把每个数分解质因数，再把这两个数公有的所有质因数和其中每个数独有的质因数全部连乘起来，所得的积就是它们的最小公倍数。

（3）短除法：把几个数公有的质因数作为除数，依次去除这几个数，直到得到的商中任意两个只有公因数1为止，然后把所有的除数和商连乘起来，所得的积就是这几个数的最小公倍数。

【例3】　求18和24的最小公倍数。

【解答】

（1）枚举法：

18和24的最小公倍数是72。

（2）分解质因数法：

18=2×3×3，24=2×2×2×3。

所以18和24的最小公倍数是（2×3）× （3×2×2）=72。

（3）短除法：

18和24的最小公倍数是2×3×3×4=72。

【例4】　用短除法计算45，75，90的最大公因数和最小公倍数。

【解答】　“短除法”是最常用的方法。

当然“分解质因数法”也比较实用，有利于分析数的组成。

【专项训练】

因数与倍数专项训练A组

一、填空题。

1.12的因数有（　　）；42的因数有（　　）。

2.50以内6的倍数有（　　），9的倍数有（　　），6和9的公倍数有（　　），其中最小公倍数是（　　）。

3.6和24的最大公因数是（　　），最小公倍数是（　　）。

4.如果A=2×3×7，B=2×5×7，那么A和B的最大公因数是（　　），最小公倍数是（　　）。

5.a和b的最大公因数是1，它们的最小公倍数是（　　）。

6.使15□成为3和5的公倍数，□里可填（　　）；使52□成为2和3的公倍数，□里可填（　　）。

二、选择题。

1.两个合数的最大公因数是1，最小公倍数是144，这两个合数是（　　）。

A.1和144　　B.9和16　　C.8和18

2.45是5和15的（　　）。

A.公倍数　　B.公因数　　C.最小公倍数

3.既是15的因数，又是30的因数的数是（　　）。

A.30　　B.60　　C.15

4.如果a÷b=7（a，b都是整数），那么a和b的最大公因数是（　　）。

A.b　　B.7　　C.a

三、求下列每组数的最大公因数和最小公倍数。

14和56　　12和8　　15和7　　28，42和21

四、解决问题。

1.一块长方形塑料板，长24厘米，宽18厘米，要把它正好分成若干个小正方形，小正方形的边长最大可以是多少厘米？至少可以分成几个这样的小正方形？

2.学生去军训，按12人一组或10人一组排队，每组都能排满且没有多余的学生，这次军训至少去了多少人？

3.18朵黄花，24朵红花，分别插在花瓶中，要使每个花瓶中黄花的朵数相等，红花的朵数也相等，且黄花、红花没有剩余，最多需要几个花瓶？每个花瓶中黄花和红花各有多少朵？

4.从小明家到学校原来每隔5米安装一根电线杆，加上两端的两根一共有25根电线杆，现在改成每隔6米安装一根电线杆，除两端的两根不需要移动外，中间有多少根不必移动？

因数与倍数专项训练B组

一、填空题。

1.1×2+2×3+3×4+…+99×100的结果是（　　）。（填“奇数”或“偶数”）

2.一个两位质数，交换个位上与十位上的数字所得的两位数仍是质数。这样的两位数有（　　）个。

3.两个数的最大公因数是21，最小公倍数是126。其中一个数是42，则另一个数是（　　）。

4.默默最近买了一个密码玩具，开锁号码顺序如下。（A，B，C，D，E，F，G，H为自然数）

A：最小的合数。　　B：既是合数又是奇数的最小数。

C：10以内最大的偶数。　　D：10以内最大的质数。

E：10以内最大的质数。　　F：既是质数又是奇数的最小数。

G：两个连续质数的和。　　H：既不是质数也不是合数，而且不是0。

你知道这个密码吗？快来猜一猜吧。（　　）

5.用若干个长10cm、宽6cm、高5cm的长方体积木搭一个正方体，至少需要（　　）个这样的长方体积木。

二、阅读材料，回答问题。

一家餐馆要想拥有更多的老顾客，菜单就要丰富。某餐馆的老板保证，一年中任何2天的菜单绝对不重复。她把菜品分为主食类、特色菜、蔬菜类、水果甜点四大类。具体如下表所示：

菜单从每一类的第一种开始排，即第一天菜单是炸薯条、烤鸭、豌豆和西瓜，次日就换到每一类的第二种。当某一类的所有菜品皆轮过一遍之后，再依序从这一类的第一种开始，例如某一天的菜单是大米饭、佛跳墙、卷心菜和水果沙拉，则次日的菜单就是炸薯条、东坡肉、四季豆和西瓜。

（1）菜单经过多久才会重复一次？

（2）餐馆生意太好了，于是老板新招聘了一名厨师。厨师自作主张，在特色菜中增加了甲鱼，蔬菜类中加入了韭菜。不料，厨师被老板辞退。有人认为，这是因为甲鱼价格高，增加了成本，惹怒了老板。其实，近年来，人工养殖的甲鱼价格已经不高了。你知道厨师被老板辞退的真正原因吗？

三、解决问题。

1.有四个孩子，他们的年龄恰好一个比一个大。他们的年龄相乘，积是3024。请你估一估，并算一算这四个孩子的年龄分别是多少。

2.美少年华朋会友，幼长相亲同切磋；杯赛联谊欢声响，念二笑慰来者多；

零天二霄志凌云，九零共庆手相握；聚起华夏中兴力，同唱移山壮丽歌。

请你将上面56个字从第一行左边第一个字起逐行逐字编为1～56号，再将号码中的质数由小到大找出来，将它们对应的字依次排成一行，组成一句话，请写出这句话。

3.有一个长为180cm、宽为45cm、高为18cm的长方体木块，将它锯成尽可能大的正方体木块（不余料）。

（1）这些正方体木块的棱长最大可以是多少厘米？一共可以锯成多少块？

（2）把这些正方体木块排成一行，长多少米？

4.书店里原有同样多的《童话故事》《百科全书》《垃圾分类知识》。开业一段时间后，《童话故事》还剩，《百科全书》还剩，《垃圾分类知识》还剩。已知这些书原来的本数在100本至150本之间，这三种书原来各有多少本？

因数与倍数专项训练C组

一、填空题。

1.20以内所有质数的和是（　　）。

2.a，b分别是不同的质数，且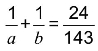。则a=（　　），b=（　　）。

3.一个六位数568abc分别能被3，4，5整除，这个六位数最小是（　　）。

4.一个质数的2倍与另一个质数的3倍之和是100，这两个质数的积是（　　）。

5.6的因数有1，2，3，6，这几个因数的关系是1+2+3=6。像6这样的数，叫完美数。通过验证，我发现28（　　）完美数。（填“是”或“不是”）

6.2012个自然数的和是奇数，那么它们的乘积是（　　）。（填“奇数”或“偶数”）

7.老大、老二、老三的年龄是三个连续的自然数，且三个自然数的积是336，则老大的年龄是（　　）岁。

8.如图，A圈内是63的因数，B圈内是42的因数，C圈内是56的因数，请在图中填上符合要求的数。

二、阅读材料，回答问题。

求两个数的最大公因数和最小公倍数，如果两个数都比较大，不容易看出它们的质因数，我们可以选择“辗转相除法”。

求三个数的最大公因数，可以先求出其中两个数的最大公因数，然后再求出这个最大公因数与第三个数的最大公因数，最后求出的就是这三个数的最大公因数。求几个数的最小公倍数也可以使用类似的方法。

请你试一试：计算（1085，1178），[1085，1178]，（1573，1547，1859）。

三、解决问题。

1.数学老师将62个正方体学具和75个长方体学具分给若干个小组，每个小组分得的正方体学具和长方体学具同样多，最后剩下2个正方体学具和3个长方体学具。请问学生最多被分成多少组？

2.12张卡片，其中3张写着1，3张写着3，3张写着5，3张写着7，你能否从中选出5张，使它们的和为20，为什么？

3.有三个正整数a，b，c，已知a与b，b与c，a与c的最小公倍数分别是525，28和300。那么a的值是多少？

4.24=2×10+4=2×（9+1）+4=2×9+（2）+（4）

2485=2×1000+4×100+8×10+5

=2×（999+1）+4×（99+1）+8×（9+1）+5

=2×999+4×99+8×9+（2×1）+（4×1）+（8×1）+（5）

因此，判断一个数是不是3的倍数，要看数字之和。

请试着用上面的方法验证一下，376是不是3的倍数。