学习整数和小数：十进制计数法和数轴规则详解

整数的认识

【知识网络】

【知识梳理】

（一）整数

1.自然数的定义

在数物体个数的时候，用来表示物体个数的0，1，2，3，4，5，…都是自然数。它可以用来表示物体的多少，即基数；也可以用来编号，表示物体的次序，即序数。

2.自然数“0”的含义

（1）“0”不仅可以表示“没有”，还可以表示特定的数值。“0”表示起点，表示正、负数之间的分界，记数时“0”有占位作用。

（2）“0”是最小的自然数，没有最大的自然数，自然数的个数是无限的。

3.整数的定义

自然数和零都是整数。整数包括正整数、零、负整数。

（二）计数法

1.计数

计数就是数数。计数的过程就是把物体与从1开始的、由小到大的自然数建立一一对应的过程。

2.计数单位

一（个）、十、百、千、万、十万、百万、千万、亿、十亿、百亿、千亿……都是整数的计数单位。“一”是基本单位。

3.十进制计数法

每相邻的两个计数单位之间的进率都是10，特点是“满十进一”。用十进制计数法所表示的数，称为十进制数。

拓展：进位制度，如二进制、八进制、十进制、十六进制、六十进制（时间）。

（三）整数数位顺序表

数级：习惯上把多位数按四位分级，即从个位起，每四个数位作为一级，个、十、百、千四位，称为个级，以此类推。

数位：各个不同的计数单位所占的位置叫作数位。例如：对于36，3在十位，表示3 个十。

位数：一个自然数所含有数位的个数叫作位数。例如：1256是四位数。

（四）整数的读法和写法

1.整数的读法

（1）万以内数的读法

读万以内的数，要从最高位起，按照数位的顺序读。千位上是几就读几千，百位上是几就读几百，十位上是几就读几十，个位上是几就读几；中间有一个“0”或连续几个“0”，都只读一个零；末尾不管有几个“0”，一律都不读。例如：3020读作三千零二十，3002读作三千零二。

（2）万以上数的读法

读万以上的数，要从最高位起，顺次读出各级里的数及它的级名。万级和亿级，都按照个级的读法去读，再在后面加上“万”字或“亿”字；每级末尾的“0”都不读，其他各数位上，有一个“0”或连续几个“0”，都只读一个“零”。例如：150000050读作一亿五千万零五十。

2.整数的写法

从高位到低位，一级一级地写，先写亿级，再写万级，最后写个级。哪一个数位上一个单位也没有，就在那个数位上写0。

（五）整数的改写与近似数

1.整数的改写

为了读写方便，可以把一个较大的多位数改写成用“万”或“亿”作单位的数。

在万位或亿位数字的右下角点上小数点，去掉小数末尾的0，再在后面加上“万”或“亿”字。例如：400000000可改写成4亿或40000万；9600000可改写成960万或0.096亿。

2.近似数

（1）近似数和准确数

准确无误地反映某些数量的真实数值，这种数叫作准确数。例如：有3个苹果，“3”是准确数。根据需要，以很接近的数值来表示统计和测量的结果，这样的数叫作近似数，或叫作近似值。例如：小芳的身高1.25 米，这里的1.25是近似数。

（2）精确度

精确度表示一个近似数近似的程度，一个近似数的近似值截取到哪一位，就说这个数精确到哪一位。

（3）求近似数的方法

3.整数的改写与省略尾数的区别

（六）整数的大小比较

比较两个多位数的大小时，先把两个多位数的相同数位对齐。

（1）如果两个多位数的位数不相同，那么位数多的数就大。

（2）如果两个多位数的位数相同，最高位上的数字大的那个数就大。如果最高位上的数字相同，从左边起第二位开始比较，以此类推，直到比出两个多位数的大小为止。例如：798320＞798319。

负数的认识

【知识网络】

【知识梳理】

（一）正、负数的定义

为了区别具有相反意义的量，我们把其中具有某一种意义的数量规定为正的，而把另一种意义相反的数量规定为负的。如收入与支出、零上温度与零下温度、东与西等，可以用正、负数来表示它们。

（二）正、负数的读写

像8，128，，2.7，…这样大于0的数叫作正数。正数前面也可以添上“+”，如：+8，+128，，+2.7等。正数前面的“+”称为正号。

像-8，，-0.9，…这样小于0的数叫作负数。负数前面的“-”称为负号。

拓展：“0”既不是正数也不是负数。

（三）正、负数的大小比较

1.数轴

规定了原点、正方向和单位长度，用来表示数的直线，就叫作数轴。

2.借助数轴比较两个数的大小

（1）在数轴上，从左到右的顺序就是数从小到大的顺序。

（2）所有的负数都在0的左边，即负数都比0小；所有的正数都在0的右边，即正数都比0大，因此负数都比正数小。

3.正、负数的大小比较

（1）所有的负数都小于正数。

（2）正数与正数比较，数值大的数就大，如5＞1；负数与负数比较，数值大的反而小，如-5＜-1。

拓展：绝对值——一个数在数轴上所对应的点到原点的距离。例如：3和-3的绝对值都是3。

互为相反数——绝对值相等，正、负号相反的两个数互为相反数。例如：3和-3互为相反数。

小数的认识

【知识网络】

【知识梳理】

（一）小数的意义

把整数“1”平均分成10份、100份、1000份……这样的一份或几份可以用分母是10，100，1000，…的分数来表示。这些分数的单位是，…，用来表示十分之几、百分之几、千分之几……的数叫作小数。

（二）小数的数位顺序表

一个小数的小数部分含有几个数位，它就是几位小数。

（三）小数的读法和写法

1.小数的读法

读小数时，整数部分按照整数的读法读，小数点读作“点”，小数部分按数位顺序从左向右顺次读出每个数位上的数字，小数点后面有几个“0”就要读出几个零。

2.小数的写法

写小数时，要先写整数部分，再写小数点，最后写小数部分。整数部分按照整数的写法来写，整数部分是零的写作“0”，然后把小数点写在个位的右下角，小数部分从十分位起，由高位到低位依次写出每一个数位上的数字。

（四）小数的性质

1.小数的性质

小数的末尾添上“0”或去掉“0”，小数的大小不变。例如：3.20=3.2。小数的性质是小数四则运算的基础。

2.小数的性质的应用

（1）利用小数的性质就可以将小数末尾的0去掉。例如：2.2300可以化简为2.23。

（2）利用小数的性质就可以将小数改写成大小不变、位数更多的小数。例如：将2.3改写成三位小数是2.300。

（五）小数点的移动引起小数大小变化的规律

小数点向右移动一位、两位、三位……小数就扩大到原数的10倍、100倍、1000倍……

小数点向左移动一位、两位、三位……小数就缩小到原数的……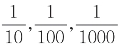

（六）小数的分类

1.按整数部分分类

纯小数：整数部分是0的小数叫作纯小数。纯小数比1小。

带小数：整数部分不是0的小数叫作带小数，也叫混小数。带小数比1大。

2.按小数部分的位数分类

（七）小数的近似数

【指点迷津】

1.一个数由4个亿、9个千万、7个百万、6个0.1和8个0.01组成，这个数是（　　），用“四舍五入”法保留一位小数约是（　　）。

【分析】此题是对数的组成、计数单位、求小数的近似数等知识的综合考查。写数时从最高位写起，将各数字写在对应的数位上，在最高位亿位和最低位百分位之间，哪个数位上一个单位也没有，就写0占位。将组成的数“四舍五入”保留一位小数，看这个数百分位上的数字是几，大于或等于5则向十分位进1，小于5则舍去。

【解答】　497000000.68　497000000.7

2.用竖式计算并验算。

2.5÷0.04

【分析】　这是一道除数是小数的除法算式，计算时要将其转化为除数是整数的除法算式。转化时，被除数2.5和除数0.04要同时扩大到原来的100倍。验算时，可以用小数乘法来验算。

【解答】　2.5÷0.04=62.5

3.简算。

4.6×32.7+54×3.27

【分析】　先把54×3.27转化成5.4×32.7，或者把4.6×32.7转化成46×3.27，这样加号两侧的乘法有相同的乘数，可以用乘法分配律进行简算。

【解答】　4.6×32.7+54×3.27

=4.6×32.7+5.4×32.7

=（4.6+5.4）×32.7

=10×32.7

=327

4.下列说法是否正确？把不正确的改正过来。

（1）大于0而小于1的小数有9个。

（2）和0.6相邻的两个小数是0.5和0.7。

【分析】　此题是对小数的意义和特征的考查。（1）在0与1之间的小数的整数部分是0，小数部分可以有一位、两位、三位……所以大于0而小于1的小数有无数个。（2）条件中没有指明和0.6相邻的小数是几位小数，和0.6相邻的一位小数是0.5和0.7，和0.6相邻的两位小数是0.59和0.61，和0.6相邻的三位小数是0.599和0.601……因此很难确定与0.6相邻的小数是哪两个。

【解答】　（1）说法不正确。大于0而小于1的小数有无数个。

（2）说法不正确。和0.6相邻的两个一位小数是0.5和0.7。（说法不唯一）

5.一个两位小数保留一位小数是8.0，这个两位小数最大是（　　），最小是（　　）。

【分析】　此题是对“四舍五入”法及求小数的近似数等知识的综合考查。

【解答】　8.04　7.95

6.去掉0.38的小数点，使它变成整数，即将原数增加（　　）倍得到；将0.38的小数点向左移动一位，即将原数减少（　　）得到。

【分析】　去掉0.38的小数点，就是把0.38的小数点向右移动两位，得到的数是原数的100倍，即原数增加（100-1）倍；将0.38的小数点向左移动一位，相当于缩小到原数的，即原数减少。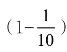

【解答】　99　

7.用估算策略解决下列问题。(www.xing528.com)

（1）7.99×9.99与80比，哪个大？

（2）妈妈带100元去书店买书，她买了两本文学书，每本20.6元，又花39.6元买了一本《汉语词典》，妈妈还想买一本家庭菜谱，有两种可供选择：薄本的13.7元，厚本的23.8元。请帮妈妈估算一下，这时她的钱够买哪一种？

【分析】　此题考查的是用估算策略解决问题的能力。

（1）把7.99看作8，9.99看作10，7.99×9.99≈8×10=80，但是把7.99看作8，9.99看作10，都把原数看大了，所以估算出的积一定比实际的积大。

（2）先用“四舍五入”法估算出妈妈买文学书和《汉语词典》后剩下的钱，再与两种菜谱的价格进行比较，最后确定可以买哪一种家庭菜谱。

【解答】　（1）因为7.99＜8，9.99＜10，8×10=80，所以7.99×9.99＜80，即80大。

（2）100-20.6×2-39.6

≈100-21×2-40

=100-42-40

=18（元）

因为13.7＜18＜23.8，所以这时她的钱够买一本薄本的家庭菜谱。

【锦囊妙计】

1.求近似数的方法

方法一：“四舍五入”法。按需要截取到指定的数位后，再看尾数的最高位，如果尾数的最高位上的数小于或等于4，就把尾数都舍去（四舍）；如果尾数的最高位上的数大于或等于5，把尾数都舍去后，再向它前一位进一（五入）。

方法二：进一法。在截取近似数时，不管尾数的最高位上的数是多少，都向前一位进一。

方法三：去尾法。在截取近似数时，不管尾数的最高位上的数是多少，都要去掉。

【例1】　一个油桶可装油100kg，装425kg油需要多少个这样的油桶？

【解答】　425÷100=4（个）……25（kg），4+1=5（个），也就是说装满4个油桶后还余25kg油。余下的油还需要1个油桶，所以本题应采用“进一法”取近似值，即需要5个油桶。

【例2】　制造一台机器需要1.2t钢材，现有39t钢材，可以制造多少台这样的机器？

【解答】　39÷1.2=32.5（台），也就是说制造32台机器后还余下0.6（因为0.5×1.2=0.6）t钢材。余下的钢材不够制造一台机器，所以应采用“去尾法”取近似值，即可以制造32台机器。

【例3】　在□里填上合适的数。

（1）38□40≈4万

（2）8□6000000≈9亿

（3）49□2300000≈49亿

【解答】　（1）0～9中任意一个数。38□40≈4万，原数千位上是8，按照“四舍五入”法，原数近似值为4万，与百位上的数字无关，所以百位上的数字是几都可以。

（2）5～9中任意一个数。8□6000000≈9亿，原数千万位上的数字要满足“五入”。

（2）0～4中任意一个数。49□2300000≈ 49亿，原数千万位上的数字要满足“四舍”。

2.整数的改写与省略尾数的方法

（1）整数的改写的方法：在要改写的数的万位或亿位右下角点上小数点，去掉小数末尾的0，再在小数后面加写“万”或“亿”字作单位。改写后的结果是一个准确数，与原数相等，要用“=”连接。

（2）省略尾数的方法：用“四舍五入”法省略指定数位后面的尾数，再在小数后面加写“万”或“亿”字作单位。省略后的结果是一个近似数，用“≈”连接。

【例4】　某一个数十万位上是最大的一位数，万位上是最小的质数，百位上是最小的合数，其余各位上都是0，则这个数写作（　　），改写成以“万”为单位的数是（　　），省略万位后面的尾数约是（　　）。

【解答】　920400　92.04万　92万

由题意可知最高位是十万位，十万位上的数字是9，万位和百位上的数字分别是2和4，其余各位上的数字都是0，所以这个数写作920400。改写成以“万”为单位的数，先在万位右下角点上小数点，然后将小数部分末尾的0都去掉，最后写上“万”字，即92.04万。省略万位后面的尾数，先从右向左数到万位，再看千位上的数字是大于等于5还是小于5，920400的千位上是0，小于5，所以省略万位后面的尾数约是92万。

3.小数点的移动引起小数大小变化的规律

【例5】　一个两位小数，若去掉它的小数点，得到的新数比原数多41.58。这个两位小数是（　　）。

【解答】　0.42

去掉两位小数的小数点，就相当于把原数的小数点向右移动了两位，这样小数就扩大到原数的100倍，增加了原数的（100-1）倍。所以原数是41.58÷（100-1）=0.42。

4.循环小数化成分数

【例6】　把分别化成分数。

【解答】　。

纯循环小数化分数，分子是由一个循环节的数字所组成的数；分母各位数字都是9，9的个数与循环节的数字的个数相同。

混循环小数化分数，分子是由小数点后面第一个数字到第一个循环节末的数字所组成的数减去不循环数字所组成的数的差；分母的头几位上的数字是9，末几位上的数字是0，9的个数与循环节的数字的个数相同，0的个数和不循环部分的数字的个数相同。

【专项训练】

整数和小数专项训练A组

一、填空题。

1.国家统计局2019年1月21日公布2018年末我国大陆总人口为1395380000人，横线上的数读作（　　），改写成用亿作单位的数约是（　　）。

2.0.7里面有（　　）个0.01，125个0.01是（　　）。

3.30500.608读作（　　）。5在（　　）位上，表示（　　）；3在（　　）位上，表示（　　）；6在（　　）位上，表示（　　）。

4.在数轴上，+7和-7到0的距离（　　），方向（　　），+7和-7相差（　　）。

5.在自然数中，最小的自然数是（　　），最小的正整数是（　　），（　　）是最大的负整数。一万里面有（　　）个（　　）；10个一万是（　　）。

6.用3个0和3个9组成不同的六位数，只读一个零的有（　　），一个零也不读的有（　　）。其中最大的一个数是（　　），最小的一个数是（　　）。

7.在里填上“＞”“＜”或“=”，在里填上符合条件的最大的数字。

二、选择题。

1.下列四个数中，最接近1亿的是（　　）。

A.1.1亿　　B.99999999

C.9999万　　D.100001000

2.4.08里面有408个（　　）。

A.十分之一　　B.百分之一　　C.千分之一　　D.万分之一

3.65840省略“万”后面的尾数约是65万中能填（　　）个数。

A.2　　B.3　　C.4　　D.5

4.下列句子中有（　　）个近似数。

（1）地球上每天约有30万人出生。　　（2）中国有34个省级行政区。

（3）我国的陆地面积约为960万平方千米。　　（4）实验小学一共有39个班级。

A.1　　B.2　　C.3　　D.4

三、操作题。

1.把下列各数在数轴上表示出来。

2.填表。（单位：cm）

四、解决问题。

1.数学考试成绩85分及以上是优秀，以85分为标准，张老师随机抽取了6名学生的成绩，记作-3分，+5分，+11分，0分，-4分，-12分。这6名学生实际分别考了多少分？

2.下面是我国四个省份（自治区）的面积。请根据要求填写。（单位：平方千米）

（1）写出表格中四个省份（自治区）的面积。这四个省份（自治区）的面积总和是（　　），总面积占我国陆地面积（我国陆地面积约960万平方千米）的（　　）%（保留一位小数）。

（2）在这四个省份（自治区）中，哪个省份（自治区）面积最大，哪个省份（自治区）面积最小？相差多少平方千米？

3.甲、乙两个数之和为373.7，乙数的小数点向右移动两位等于甲数，则甲数是多少？（用两种方法解答）

整数和小数专项训练B组

一、填空题。

1.有一个九位数，最高位上是最小的合数，百万位上是最小的正整数，千位上是最小的质数，其余各位上是最小的自然数，这个数写作（　　），读作（　　），把这个数写成以“万”作单位的数是（　　）。

2.小明在读一个数时，把小数点丢了，结果读成四万零五百零七，而原来的小数只读一个零，原来的小数是（　　）。

3.0.48里含有（　　）个千分之一，把它的小数点先向右移动三位，再缩小到它的（　　）后是0.036。

4.暑假里小明想去外公家住几天，到车站后，小明想打电话让外公来接他，但他只记得外公家的电话号码是6272734，小明至少试（　　）次，才能保证打通外公家的电话。

5.一个五位数，十位上的数字是6，是个位上的数字的2倍，最高位是最大的一位数，前三位数字的和与后三位数字的和都是18。这个五位数是（　　）。

二、判断题。

1.1亿里有10个一千万，或有1000个一百万。　　（　　）

2.大于0.57而小于0.67的小数有10个。　　（　　）

3.一个五位数，最高位上的计数单位是万位。　　（　　）

4.保留两位小数是1.30，保留三位小数是1.291。　　（　　）

三、选择题。

1.两数相乘，积是28.4。如果两个乘数分别缩小到原来的，那么积是（　　）。

A.2.84　　B.0.284　　C.284　　D.2840

2.将大长方形看作单位“1”，阴影部分用小数表示是（　　）。

A.0.25　　B.0.45

C.0.375　　D.0.4

3.近似数是8.00的数的取值范围是（　　）。

A.7.995～7.999　　B.7.989～7.995　　C.7.990～7.999　　D.无法确定

4.在混循环小数中，移动循环节的第一个圆点，使产生的循环小数尽可能小，循环节应含有（　　）。

A.8个数字　　B.6个数字　　C.3个数字　　D.4个数字

四、计算题。

2006×2007-2005×2008　　30.05×19+300.5×4.1+15.025×80

10.54×1.75+0.825×5.4

五、解决问题。

1.把一个数的小数点向右移动两位，所得的数比原数大27.72，那么原数是多少？（先画简单的线段图，再列式解答）

2.用卡片摆出不同的小数。

（1）摆出大于1而小于5且末尾不是“0”的三位小数。

（2）摆出有两位小数的最小的数。

（3）摆出零不读出来的小数。

整数和小数专项训练C组

一、填空题。

1.如果把4.5的整数部分记作a，小数部分记作b，那么3a+3b的值是（　　）。

2.把4÷7的商化为循环小数是（　　），小数点后第1000个数字是（　　）。

3.把0.67万改写成用“一”作单位的数，写作（　　）。

4.把0.96的小数点先向左移动两位，再向右移动一位，得到（　　）。

5.在里填上“＞”“ ＜”或“=”。

二、计算题。

三、解决问题。

1.用3个不同的数字（0除外）能组成6个不同的三位数，这6个三位数的和是3552，这6个数中最小的数是多少，最大的数是多少？

2.循环小数的小数点后面第1位到第2015位上的所有数字之和是多少？

3.会计记账时，由于粗心，把一笔钱的小数点点错了一位，结果多出了51.12元，原来这笔钱有多少元？

4.在由数字0，1，2，3，4，5，6，7组成的三位数中：

（1）可组成多少个不同的三位数（数字互不相同）？

（2）可组成多少个不同的三位数（数字可以相同）？

（3）可组成多少个各位数字互不相同的四位数奇数？

（4）可组成多少个各位数字互不相同的四位数偶数？