套期保值比率与凸度效应的关联分析

科尔布等（1981，1982）提出了一个用于对固定收益证券进行套期保值的基于久期的套期保值比率。他们的套期保值比率为：

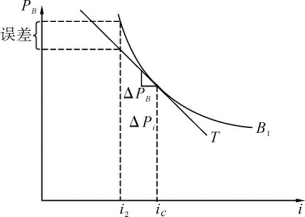
图6-1　显示利率变化时凸度对债券价格的影响

上式中，Dj为第j个工具的麦考利久期，麦考利久期定义为：

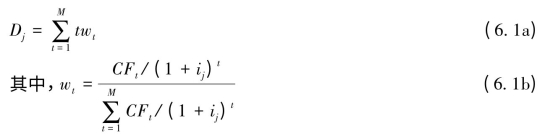
CFt——时间t的现金流（息票或息票加上本金）；

t——时间期数（一般每半年为一期）；

M——工具的到期时间，以期数计；

Pj——工具j的价格；

ij——工具j的以半年计的到期收益率；

j对现金债券而言为B，对期货合约而言为F。

方程（6.1b）的分母为债券的现值。麦考利久期的前提假定为收益率曲线是水平的，并且收益率曲线的变化表现为平行移动。

盖伊和科尔布（1983），波波维奇和高斯曼（2012）通过一些例子说明了如何运用该套期保值比率。然而，麦考利久期的前提假定是利率只发生小的变化（或者说，利率与债券价格之间是线性关系）。从图6-1可看出，如果利率发生大的变化，久期对债券价格变化的估计是不准确的。^[2]该错误产生的原因是，当利率发生变化时，久期也发生了变化，或者说，债券价格线B1的切线的斜率也发生了变化。

用久期进行套期保值时，有人可能认为用于估计债券价格变化的久期所引起的误差可以被用于估计期货价格变化的久期所引起的同等误差所抵消。但是，用久期进行套期保值所引起误差的大小取决于被套期保值债券的特征与套期保值工具的特征之间存在着多大程度的差别。如果二者之间的特征不同，那么比率DB/DF、PB/PF以及（1+iF）/（1+iB）会随着利率的变化而出现很大的变化。引起误差的主要原因在于债券价格与利率之间存在着非线性关系（即凸度），凸度定义为：

(www.xing528.com)

上式中，Cj为工具j的凸度，wt的含义已在方程（6.1b）中定义。

从图6-2和图6-3可看出，用久期进行套期保值，在凸度不相同时，会出现怎样的错误。图6-2显示了现货债券（B1）的价格曲线以及国债期货合约（B2）的价格曲线。与久期一样，固定收益工具的凸度取决于它们的到期日、息票以及收益率。^[3]很显然，在图6-2中，即使在ic处使用了久期套期保值，当利率从ic变化到i2时，因B1和B2的凸度不同，也会引起套期保值误差。在ic处的久期套期保值抵消了利率变化所引起的一阶效应（久期效应），但是，由于没有对固定收益工具与用于套期保值的期货合约的凸度的差别进行套期保值，二阶效应（凸度效应）所引起的误差仍然存在。引起误差的原因显示在图6-3中，即：由于利率从ic移动到i2，两条价格曲线在i2处的久期并不相同，也就是说，两条价格曲线对利率的变化有着不同的敏感性。

表6-1显示，对于有着不同特征的现货债券和期货合约来说，当利率变化时，如用久期套值方法进行套期保值，为什么会出现误差。表中的最后三列显示了误差产生的原因，也即是，当利率变化时，二者的相对久期会发生变化，正是由于这个原因引起了套期保值比率应发生相应的变化。

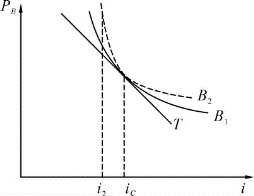
图6-2　显示凸度不同对债券价格的影响

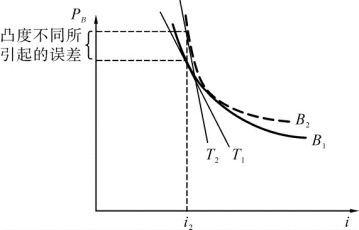
图6-3　凸度不同时，利率变化后久期会不同

表6-1　凸度对套期保值结果的影响（每1000元面值）

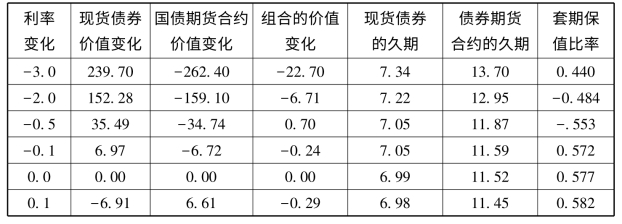
续表

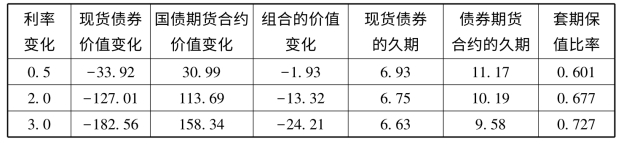
表6-1比较当利率变化时，现货债券及期头货头寸的价格变化和久期。通过本表可以说明为了提高套期保值的效果，需要将凸度作为套期保值的一部分。国债期货合约是持有久期为11.52年的空头头寸，套期保值比率为0.577。现货债券的息票率为、到期时间为10年、久期为6.99年。

避免由于凸度的不同导致久期随利率的变动而变动的方法是，使用既考虑久期效应又考虑凸度效应的套期保值方法。Goodman和Vijayaraghavan（1987、1989）提出了一个两工具套期保值方法，该方法令现货债券与两种固定收益期货合约的久期与凸度相等。他们提出的套期保值比率是^[4]：

上式中，Hj为j的套期保值比率，LTF为长期固定收益期货合约，STF为短期固定收益期货合约，B为现货债券工具。

简单地令久期和凸度相等似乎是消除一阶和二阶效应的合乎逻辑的方法。但是，应该注意的是，为了使现货-期货头寸组合的净价格变动最小化，我们应该让价格变动相匹配，而不是让久期和凸度相匹配。下一部分将提出一个符合该要求的两工具套期保值比率。