我国商业银行利率风险状况实证分析：基于银行收益支出视角

5.2.1　对利率风险进行实证研究的方法

国外对商业银行利率风险状况进行实证分析的文献很多，研究方法大致可分为三种。第一种方法是，通过分析利率变动与商业银行股票收益率之间的关系来推断商业银行的利率风险状况。第二种方法是，通过分析商业银行资产和负债的久期是否匹配来推断商业银行的利率风险状况。第三种方法是，通过分析商业银行的收益、支出与利率变动之间的关系来推断商业银行的利率风险状况。

国外对商业银行利率风险进行实证分析的三种方法中，第一种方法需要上市银行股票价格的数据。第二种方法需要银行每笔资产和负债到期的准确时间的数据，一方面，有些资产和负债没有确切的到期日，如活期存款、通知存款等，另一方面，在我国，即使有确切到期期限的资产和负债的到期日，对银行的外部人员来说是不可得到的。因此，本节用第三种方法对我国商业银行利率风险状况进行实证分析，下一节用第一种方法对我国商业银行利率风险状况进行实证分析。

5.2.2　模型、数据和估计方法

本章运用以下模型分析我国商业银行的利率风险状况。

商业银行的名义利息收入可表示为：

上式中，GIIt表示本期利息收入，rat表示本期贷款利率，TAt表示本期资产，TAt-1表示上期资产，g［rat，TAt-TAt-1］表示新增资产在本期获得的利息收入，这部分应该只对当前利率敏感。原有资产在本期获得的利息收入用表示，原有资产在本期获得的利息收入仅仅是原有资产在本期到期并重新投资的这部分对当前利率敏感。假设原有资产的目标收益用线性形式表示如下：

用下式表示原有资产的实际收益与目标收益之间存在着滞后：

由上式可得到：

（5.1）式右边的第一项可近似地表示为：

上式中φ反映了新增资产的平均增加速度，如果新增资产在本期以固定的速度增加，那么φ=0.5。将（5.4）式和（5.5）式代入（5.1）式，并在方程两边同除以TAt-1可得到：

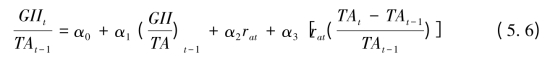
为了用于计量模型，将（5.6）式改写为：(www.xing528.com)

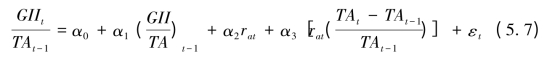
上式中系数的预期符号为：

类似地，可得到估计利息支出对利率变动敏感性的模型：

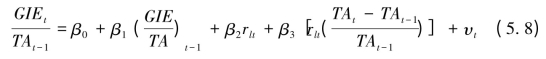
上式中，GIIt表示本期利息支出，rlt表示本期存款利率，其他符号的含义与（5.7）式相同。系数预期的符号为：

以上模型中系数的估计值提供了商业银行利率风险大小状况的信息。系数α2和β2分别反映了利率变化对利息收入和利息支出的初始影响，如果α2=β2，那么表明当贷款利率和存款利率发生同等变化时，商业银行在短期内的利息收入变动与利息支出的变动互相抵消，短期净利息收入的变动不受利率变动的影响；如果α2＞β2，那么表明当贷款利率和存款利率发生同等幅度的下降时，在短期内利息收入的下降幅度会大于利息支出的下降幅度，银行将遭受净利息收入下降的风险；如果α2＜β2，那么表明当贷款利率和存款利率发生同等幅度的上升时，在短期内收入的上升幅度会小于利息支出上升的幅度，银行会遭受净利息收入下降的风险。

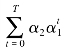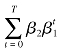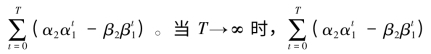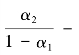
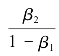上面模型中的系数α1和β1分别反映了资产和负债对利率变化的调节速度。利息收入对贷款利率的一次永久性变动存在着一定的滞后，滞后值的大小既受调节速度α1的影响，又受初始影响α2的影响。贷款利率的一次永久性变化对T期累积的利息收入的影响为。类似地，存款利率的一次永久性变化对T期累积的利息支出的影响为。从而，如果贷款利率和存款利率发生相同幅度的一次永久性变动，对T期累积的净利息收入的影响为成为。如果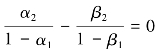，则贷款利率和存款利率发生同等变动时，商业银行在长期中的利息收入变动与利息支出的变动互相抵消，长期净利息收入的变动不受利率变动的影响；如果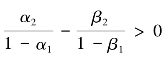，那么表明当贷款利率和存款利率发生同等幅度的下降时，在长期中利息收入的下降幅度会大于利息支出的下降幅度，银行将遭受净利息收入下降的风险；如果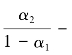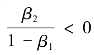，那么表明当贷款利率和存款利率发生同等幅度的上升时，在长期中利息收入的上升幅度会小于利息支出上升的幅度，银行会遭受净利息收入下降的风险。

本章研究的数据来自于《中国金融年鉴》，数据期间从1995年至2015年。1995年的《中国金融年鉴》报告了13家商业银行的资产负债表和损益表，但由于某些银行报告的数据的统计口径不一致，无法得到有用的数据。如中国工商银行从1998年起对系统内往来款项、联行往来收支均轧差报告，与1998年前报告的数据统计口径不一致，无法采用；交通银行从2000年起对统计口径作了调整；上海浦东发展银行1999年年鉴与1998年年鉴中报告的1997年损益表中的数据差别很大，虽然未作说明，应该是统计口径调整所致。故本章只选取其中的7家商业银行进行研究，即中国农业银行、中国银行、中国建设银行、光大银行、广东发展银行、中信实业银行和深圳发展银行。

利率数据是取年度利率的平均值，用百分比表示。资产利率取一年期贷款法定利率，负债利率取一年期存款法定利率。如利率采用半年期的贷款利率和存款利率，得到的结果与采用一年期利率所得到的结果非常接近。GIIt和GIEt是年度的利息收入和年度的利息支出。

由于模型（5.7）、（5.8）中忽略了一些不可观测到的解释变量，这些不可观测的解释变量可能同时影响方程（5.7）和（5.8），方程（5.7）中的干扰项和（5.8）中的干扰项很可能是相关的。对于每家银行，我们用Zellner的似无关回归方法同时估计方程（5.7）和（5.8）。该估计方法的标准误差比用普通最小二乘法估计的标准误差更小。由于方程（5.7）和（5.8）中存在着滞后的因变量，干扰项之间可能是自相关的，这会引起对方程系数和标准误差的估计产生偏误。为了避免这种可能性，每个方程采用Cochrane-Orcutt的迭代法进行估计。

5.2.3　模型检验结果

模型回归分析的结果见表5-1。模型很好地适合了数据，在全部回归方程中，除一个回归方程的调整的R2的值为0.92以外，其余的调整的R2的值均大于0.95。系数α2与β2之差α2-β2衡量了当存款利率和贷款利率均变动一个百分点时，短期内净利息收入变动占总资产的百分比。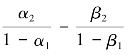衡量了当存款利率和贷款利率均永久性地变动一个百分点时，从长期来看，累计净利息收入变动占总资产的百分比。从表5-1中可以看出，7家银行中，有五家银行的α2-β2的值在5%的显著水平上是异于零的，有6家银行的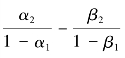的值在5%的显著水平上是异于零的。如果按2003年资产总值是否大于1万亿元把7家银行分为两类，属大型银行的有3家：农业银行、建设银行、中国银行；属中等银行的有其余4家。3家大型银行中，有一家银行的α2-β2显著异于0，其均值为0.1；4家中等银行中，有4家银行的α2-β2的值显著异于0，其均值为0.47。3家大型银行中，有两家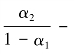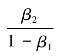的值显著异于0，其绝对值的平均值为0.37；4家中等银行中，有4家银行的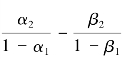的值显著异于0，其绝对值的平均值为0.66。表中还列出了1995—2003年各家银行的净利差收入占总资产的百分比的平均值。

表5-1　回归模型的估计结果

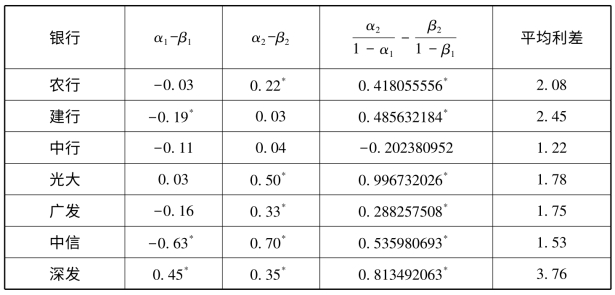
注：*表示值在5%的显著水平上异于0。

从以上计量模型的结果可以看出，我国商业银行从总体上说抗利率风险的能力并不强，利率的波动不管是对银行的短期净利息收入还是长期净利息收入都有较大的影响。其中，中等银行的利率风险暴露比大型银行的利率风险暴露更大。