比较2.5幂久期方法与传统的久期加凸度方法

第二部分和前面的数字例子已表明，传统的久期方法可以通过在估计时加上债券价格的泰勒展开式的第二项（即凸度）加以改进。导数的第二项减少了估计误差的绝对值，与传统的久期方法相比较，久期加凸度方法的估计结果更准确。但是，当利率上升时，由传统的久期加凸度方法得到的债券价格的估计值要大于债券价格的真实值。估计价格过高的原因在于债券价格对收益率的导数的第三项是负值。

传统久期加凸度方法对债券价格的过高估计对风险回避型的投资者来说是不利的。与利率下降所引起的债券价格上升所带来的利益相比较，风险回避型的投资者更关注利率上升所引起的债券价格下降所带来的不利影响。也就是说，与债券价格上升同等幅度相比较，债券价格下降是更不愿看到的。然而，幂久期方法的估计值总是小于真实价格，因为债券价格的自然对数对到期收益率的导数的第二项总是正值。

虽然在多数情况下，传统的久期加凸度方法所导致的误差要比幂久期方法所导致的误差小，但二者之间的差别是很小的。图2-2以到期时间为30年、息票率为5%的平价债券为例，对传统的久期方法、幂久期方法和传统的久期加凸度方法所引起的误差进行了比较。与传统的久期方法相比较，幂久期方法要准确得多。当利率下降时，由幂久期方法所导致的误差要比由传统的久期加凸度方法所引起的误差稍大，当利率上升时误差绝对值的差距与利率下降时误差绝对值的差距相近。当利率上升引起债券价格下降时，幂久期方法提供了一个更保守的估计。这一点正是幂久期方法的优势。

图2-3显示了30年期零息票债券的估计误差。与传统的久期加凸度方法以及传统的久期方法相比较，幂久期方法的估计误差要小得多。图2-4显示了永久债券的估计误差。与图2-2中一样，幂久期方法的估计值比传统久期方法的估计值要准确得多。当利率下降时，幂久期方法的估计误差比传统的久期加凸度方法的估计误差要大；当利率上升时，幂久期方法的估计误差与利率下降时的估计误差相近。但与传统的久期加凸度方法相比，幂久期方法的估计价格要低于实际价格。

将由幂久期方法及传统久期加凸度方法所产生误差的绝对值占真实价格的百分比进行大量的数字比较，可以发现，即使在利率变动3%时，由两种方法所产生的误差的差别程度总是小于真实价格的2%。在图2-5、图2-6和图2-7中，我们以息票率为5%的平价债券、息票率为10%的平价债券和到期收益率为5%的零息票债券，在各种到期时间和各种利率变化情况下为例，画出了两种方法的估计误差的绝对值的差占真实价格的百分比。如果差是正值（负值），幂久期方法的估计值有更大的（更小的）误差。

图2-5和图2-6以到期时间从零至30年、息票率分别为5%和10%的平价债券为例，比较了由幂久期方法所产生的误差和由传统久期加凸度方法所产生的误差。在这两个图形中，幂久期方法所产生的误差都比传统久期加凸度方法所产生的误差稍大，到期时间越短，两种方法所产生的误差的差别程度也越小。

图2-5　比较用幂久期方法和传统久期加凸度方法估计年息票率为5%的平价债券时的误差(www.xing528.com)

图2-5假想一个年息票率为5%的平价债券。到期时间轴变化从1年到30年，到期收益率轴变化从-3%到3%。垂直轴给出用幂久期方法和传统久期加凸度方法估计误差的绝对值占真实价格的百分比之差。如果显示在垂直轴的差为正值（负值），幂久期方法估计误差的绝对值更大（更小）。因此，如果垂直轴的读数为0.02，表明幂久期方法估计误差的绝对值占真实价格的百分比，比传统久期加凸度方法估计误差的绝对值占真实价格的百分比大2%。

图2-7以到期收益率为5%、到期时间从零至30年的零息票债券为例对两种方法所产生的误差进行了比较。幂久期方法总是比传统久期加凸度方法的准确程度更高（因为差是负值）。与传统久期加凸度方法相比，利率上升时，幂久期方法的准确程度更高；到期时间越长，幂久期方法的准确程度也越高。概括起来说，这些图形清楚地表明，幂久期方法的误差的绝对值与传统久期加凸度方法的误差的绝对值非常接近。当利率下降时，幂久期方法与传统久期加凸度方法几乎一样准确。当利率上升时，幂久期方法的估计误差的绝对值与利率下降时估计误差的绝对值很接近，但它没有过低地估计价格的下降。

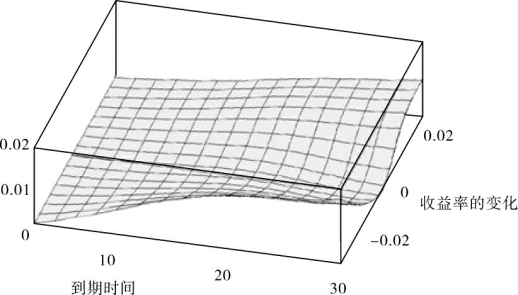
图2-6　比较用幂久期方法和传统久期加凸度方法估计年息票率为10%的平价债券时的误差

图2-6假想一个年息票率为10%的平价债券。到期时间轴变化从1年到30年，到期收益率轴变化从-3%到3%。垂直轴给出用幂久期方法和传统久期加凸度方法估计误差的绝对值占真实价格的百分比之差。如果显示在垂直轴的差为正值（负值），幂久期方法估计误差的绝对值更大（更小）。因此，如果垂直轴的读数为0.015，表明幂久期方法估计误差的绝对值占真实价格的百分比，比传统久期加凸度方法估计误差的绝对值占真实价格的百分比大1.5%。

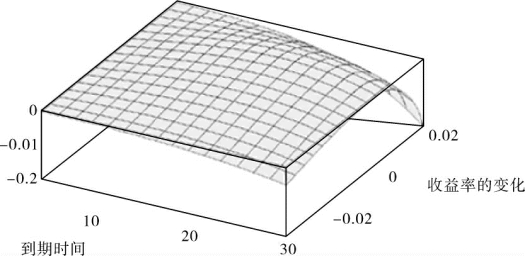
图2-7　比较用幂久期方法和传统久期加凸度方法估计到期收益率为5%零息票债券时的误差

图2-7假想一个到期收益率为5%的零息票债券。到期时间轴变化从1年到30年，到期收益率轴变化从-3%到3%。垂直轴给出用幂久期方法和传统久期加凸度方法估计误差的绝对值占真实价格的百分比之差。如果显示在垂直轴的差为正值（负值），幂久期方法估计误差的绝对值更大（更小）。因此，如果垂直轴的读数为0.05，表明幂久期方法估计误差的绝对值占真实价格的百分比，比传统久期加凸度方法估计误差的绝对值占真实价格的百分比大5%。