【摘要】：如果我们将债券价格的对数对收益率求导，可得到负的修正的久期：表2-3息票率为5%的永久债券表2-3显示了年息票率5%的永久债券的价格敏感性。第六列给出了用幂久期方法估计的新价格。从概念上看，两种近似方法都是可行的，但更准确的方法是更好的近似方法。从方程（2.9）可得到：上式可写成：新价格可近似地写成：价格的百分比变化可近似地表示成：因为在上面的式子中，幂中含有修正的久期，我们称它为幂久期方法。
有几位学者指出：债券价格的自然对数是测度利率变化时债券价格的百分比变化的一个更好的方法。基于这些思想，本章提出一个简单但准确程度很高的测度利率变化时债券价格百分比变化的方法。如果我们将债券价格的对数（lnP）对收益率（Y）求导，可得到负的修正的久期（D）：
表2-3 息票率为5%的永久债券
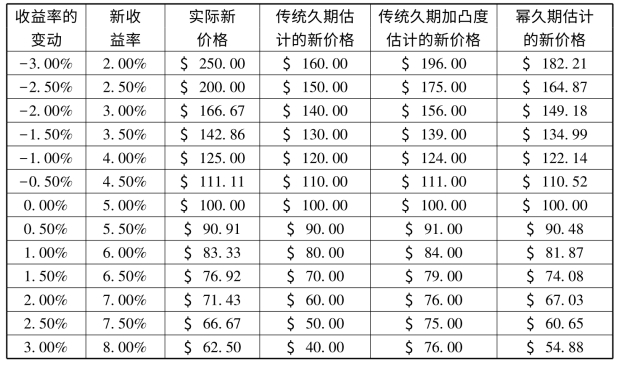
表2-3显示了年息票率5%的永久债券的价格敏感性。修正的久期（D）为20，凸度（C）为400。第三列给出了到期收益率（YTM）变化后债券的实际价格。第四列给出了用传统久期方法
估计的新价格。第五列给出了用传统久期加凸度方法
估计的新价格。第六列给出了用幂久期方法
估计的新价格。
整理后得：
如果用ΔY近似地代替dY，则有：
我们近似地以Δ（lnP）代替d（lnP），则有：
(www.xing528.com)
上式中P0为初始价格，
是利率变化后新价格的近似值。
方程（2.9）用债券价格的自然对数的变化作为债券价格百分比变化的近似值。传统的久期是测度债券价格百分比变化的另一个方法，它用债券价格变化的近似值除以初始的价格。从概念上看，两种近似方法都是可行的，但更准确的方法是更好的近似方法。稍后，可以看到用自然对数的变化作为债券价格百分比变化的测度，是一种更准确的近似方法。
从方程（2.9）可得到：
上式可写成：
新价格可近似地写成：
价格的百分比变化可近似地表示成：
因为在上面的式子中，幂中含有修正的久期（D），我们称它为幂久期方法。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
