传统估计方法

对于平坦的期限结构，到期时间为T的债券或固定收益资产的价格可表示成以到期收益率（Y）为贴现率的息票（C）和平价（Par）的现值，即：

在下面的分析中，为简单起见，我们用“债券价格”这一术语，但下面分析的结果对所有固定收益资产都是成立的。如果我们取债券价格（P）相对于到期收益率（Y）的一阶导数，并除以P，我们可得到负的修正的久期（D）：^[2]

修正的久期提供了利率变化时债券价格百分比变化的近似估计。用修正的久期估计债券的百分比变化为：

上式中P0为初始价格，为新价格的估计值，ΔY为利率的变动值。对上式进行整理得：

表2-1、表2-2和表2-3给出了用传统久期方法估计三种不同的债券价格的例子，三种债券分别为：平价债券、零息票债券和永久债券。例如，表2-1中显示30年期、年息票率为5%的平价债券的修正的久期为15.37，表2-1也显示了实际的新价格（第3列）和用传统的修正的久期方法估计的新价格（第4列）。当利率上升50个基本点时，根据方程（2.4）估计出的新价格为92.31美元，与实际的新价格92.73美元很接近。

然而，当利率变化较大时，用传统久期方法进行估计得到的估计值不是很准确。例如，表2-1中，如果利率上升3%，估计的新价格为53.88美元，与实际的新价格66.23美元相差很大。

为了得到更好的估计，金融实践者往往用凸度将传统的久期估计方法修改如下：(www.xing528.com)

上式中，，为凸度。是由进行凸度修正后的传统久期方法估计出的新价格。C，即凸度，等于债券价格的二阶导数除以2P0。

用凸度修正后，估计值的误差更小，特别是当利率发生较大的变化时。表2-1、表2-2和表2-3的第5列给出了用传统的久期加凸度方法得到的估计值。对于30年期、息票率为5%的平价债券，凸度值为175.23。当利率上升3%时，用传统的久期

表2-1　息票率为5%的30年期平价债券

表2-1显示了年息票率为5%、到期时间为30年的平价债券的价格敏感性。修正的久期（D）为15.37，凸度（C）为175.23。第三列给出了到期收益率（YTM）变化后债券的实际价格。第四列给出了用传统久期方法估计的新价格。第五列给出了用传统久期加凸度方法估计的新价格。第六列给出了用幂久期方法估计的新价格。

加凸度方法得到的新价格的估计值为69.65美元。与仅用久期方法得到的估计值相比，用久期加凸度方法得到的估计值与实际新价格要接近得多。

然而，通过比较表2-1、表2-2和表2-3中的第三列和第五列可以看到，当利率上升时，用传统久期加凸度方法过高地估计了债券的价格。对于风险回避型的投资者而言，对债券价格的过高估计是不利的，因为他们的头寸在利率上升时实际遭受的价格下降比用传统久期加凸度方法给出的估计值要大。因此，传统久期加凸度方法过低估计了利率上升时价格下降的风险。

表2-2　30年期零息票债券

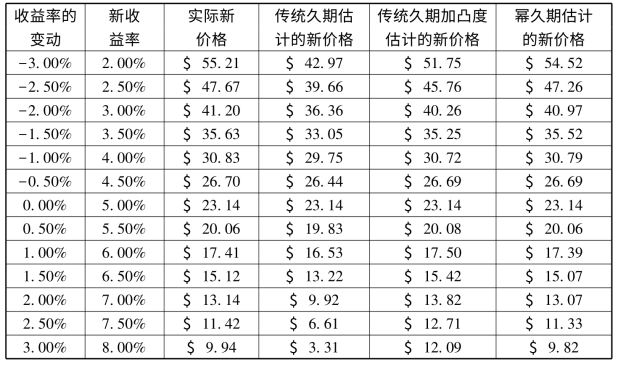
表2-2显示了30年期零息票债券的价格敏感性。修正的久期（D）为28.57，凸度（C）为421.77。第三列给出了到期收益率（YTM）变化后债券的实际价格。第四列给出了用传统久期方法估计的新价格。第五列给出了用传统久期加凸度方法估计的新价格。第六列给出了用幂久期方法估计的新价格。