规律探寻：糖水不等式等比放缩法应用指南

(一)概述

基本放缩结构1

基本放缩结构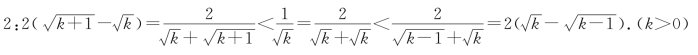

基本放缩结构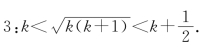

基本放缩结构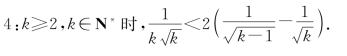

数列不等式放缩技巧操作指南：

①数列不等式一般都有一定的结构特点，要会判断数列不等式的结构模型；

②不同的结构有不同的放缩方向与方法，要积累结构模型及相应的放缩技巧；

③放缩有一些基本类型，但问题主干向着基本类型转化是前提，要具备转化的意识；

④数列不等式中一般含有通项，要抓住通项的结构特点，进行适当的变形，为放缩技巧的应用奠定基础；

⑤放缩过程有一系列的操作，必须掌握放缩过程中的操作顺序.

(二)常用方法

(1)函数放缩法(构造函数，利用函数单调性进行放缩)(www.xing528.com)

基本结论：lnx≤x－1等价于ln(1＋x)≤x.

(2)裂项放缩法

裂项放缩法是最广泛、最重要的放缩技巧之一，常见于积式、分式、根式、二次等结构，基本思想是转化成差形结构ƒ(n)－ƒ(n－1)累加求和解决问题，一般思路是配积、取倒、凑差.

基本结论：若a－b＝mab，则

ƒ(1)－ƒ(n)＝ƒ(1)－ƒ(2)＋ƒ(2)－ƒ(3)＋…＋ƒ(n－1)－ƒ(n).

a1 ＋a2 ＋… ＋an ＜ƒ(n ＋1)的裂项放缩思路：先证an ＜ƒ(n ＋1)－ƒ(n)，再累加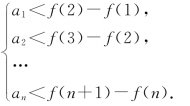，得

a1＋a2＋…＋an＜ƒ(n＋1)－ƒ(1)≤ƒ(n＋1)，只要判断ƒ(1)≥0即可.

(3)对偶放缩法

基本结论：糖水不等式

(4)等比放缩法

等比放缩适用于指数结构，当后、前项不是纯等比关系，可以考虑将后、前项的比值放缩成一个常数，转化为等比数列求和处理.

基本结论：正数列中