朱载堉十二平均律的等比数列数学理论

时间：2023-07-21 理论教育版权反馈

【摘要】：为纪念这位为人类科学文化作出了杰出贡献的历史人物，这里就他十二平均律的等比数列数学理论，谈谈自己的浅见。朱载堉在创建十二平均律所做的数学工作，无疑具有上述所有关于数学理论的这些内容和特点。在这样的比数或数列中的某项数值，被称为某项率数或简称为某项之率。他将十二平均律各律率称为密率。约率、密率的划分是律率概念的进一步深化，为十二平均律的等比数列理论准备了必要的基本数学概念。

朱载堉十二平均律的等比数列数学理论

◎黄国玺

（1937.11- ）原四川音乐学院附中高级讲师。

关键词：朱载堉率等比数列十二平均律

朱载堉（1536—1611）在明万历九年正月吉日（1581年2月6日）之前，已经完成了人类音乐文化史上建立十二平均律的创举。①在创建十二平均律理论的同时，他横跨自然科学与艺术科学，除了在音乐、天文历法、声学和物理、舞蹈、文学等众多学科领域取得累累硕果外，特别在数学上表现出非凡的创造精神，取得一系列世界第一的成就。为纪念这位为人类科学文化作出了杰出贡献的历史人物，这里就他十二平均律的等比数列数学理论，谈谈自己的浅见。

所谓数学理论，主要指使用数学概念与逻辑方法，对数学公式、方法进行推理、证明。主要表现为对概念给予科学的定义，对所作的判断、公式给予合乎逻辑的论证。朱载堉在创建十二平均律所做的数学工作（包括他在等比数列方面的数学工作），无疑具有上述所有关于数学理论的这些内容和特点。

一、“率”的概念的运用与深化

为研究发音体（弦、管等）长度、面积、体积的需要，朱载堉引进了圆、圆柱、立方体等有关几何图形概念，研究了圆周、半径、直径、内接正方形、外切正方形间的数量关系，对平方、立方、开平方、开立方、幂、积等众多概念给予了科学定义。例如他对平方幂所作定义：“平方谓之幂，立方谓之积”，“算术自乘，其数必方，纵横正等有类乎幂”②等，可说与今日定义无异。

在音高频率尚未发现之时，音高的相对高度，几乎只有通过管弦的长度比值来给予衡量，因而“率”的数学概念在确定相对音高上起着重要作用，历来受到律学家的重视。汉蔡邕（132—192）曾在《月令章句》中这样写道：“律者，率也，……律者，清浊之率法也。声之清浊，以管之长短为度。律谓之分，言其长短有分度也。”就清楚地说明了音律的高低与音高间相互比较，由发音体长短与其比率来确定。

中国古算的“率”，是指有一定相比关系的两个数或一列数。例如三国时魏刘徽在注《九章算术》中就定义道：“凡数相与者谓之率”，并说：“令每行为率”。就是说有“相与”关系——相当于今天的相比关系的两数或数列，被称为率③。在这样的比数或数列中的某项数值，被称为某项率数或简称为某项之率。

律率，就是指按一定生律方法与程序所得到的有一定相比关系的音律数列。例如按“三分损益法”生律，就是以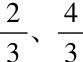为生律率，上下依次生得各律率数，不论这些律率数是按音高顺序还是按相生顺序排列，各律率数之间总是具有一定相比关系的。因而律率实是率概念在律学领域的运用与具体化。

一组率数具有这样的性质：各率数扩大或缩小不为零的同样倍数，它们之间原有的比例关系不变；律率也具有同样的这一性质。

朱载堉正是准确地运用了率及其性质，解决了一系列律学难题。其中，他以率的概念澄清了历史遗留下来的律尺、度尺标准不一所造成的混乱；运用率的性质，成功的在世界首次提出九、十两种进位制小数互化的原则与计算方法，取得了突出的成就。在朱氏之前，何瑭（1474—1543）已认识到，律度混乱产生的原因，是自《汉志》未能区分黄钟音律一尺被划分为九寸，与度量一尺被划分为十寸而开始的。朱氏说：“《汉志》谓黄钟之律九寸，加一寸为尺。……若加一寸以为尺，则又何取于黄钟？殊不知黄钟长，固非人所能为。至于九其寸而为律，十其寸而为尺，则人之所为也。”⑤朱载堉除根据上古“同律度量衡”断定“度本起于黄钟之长，则黄钟之长即是一尺”。⑥⑦此外，更加明确地指出：将黄钟一尺划分为九寸是为了三分损益算律无不尽小数，使之保持整数。而之所以能够这样做，其根据是由率的性质所决定，只要各律保持应有比例关系，黄钟可假设任意率数，当然黄钟律率可定为九，其度量尺亦可定为十。朱载堉写道：“所谓长九寸，长八寸十分一之类，盖算家立率耳。”⑧“夫率者，算经假如之法也，……古称黄钟九寸，其数八十一，此亦算率耳。”⑨这样，他在澄清上千年律度混乱的问题中，以率的概念与性质的运用，为确立九、十两种进位制小数互化找到了数学理论依据。他在律度互求法则“从微至著，用九乘除”⑩，以及律度互化的计算规范化程序的叙述中，都贯穿了率的性质的运用。

朱载堉还提出了“约率”、“密率”两个重要数学概念。“约率”、“密率”二词，较早运用的有南北朝祖冲之（429—500），他将圆周率π的近似比数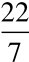称约率，π的另一近似程度较高的比数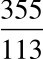称密率。朱氏所提约率、密率，广义来讲是指各律之间长度、管径、体积的比例关系而言，狭义来讲是对各律之间的长度率数及律率数而言，本文仅谈狭义。他将所有不能返回黄钟的律率数列或各律率统称为约率，其中包括三分损益所生各律之率。他说：“古法颇疏，得其大略而已，非精密之算术，故谓之约率也。”○1他将“749”法所生各律亦称约率，因其所生律率不能返回黄钟。他将十二平均律各律率称为密率。他特别指出约率“749”法与密率根本不同，他说：“约率所谓七百四十九，即密率所谓七亿四千九百万有奇也。有奇是以密，无奇是以疏，此自然之理耳。”⑫他在此先指明约率“749”与密率的近似值关系，然后明确指出有奇是以密，无奇是以疏，两者截然不同，泾渭分明，不容相混。约率、密率的划分是律率概念的进一步深化，为十二平均律的等比数列理论准备了必要的基本数学概念。

二、“三分损益”不能返回黄钟的数学证明

“三分损益法”生律十二次不能返回黄钟，继续往下生律是否能返回呢？朱氏之前，从这一思路考虑的有汉京房（前77—前37）生六十律，有南北朝钱乐之（420—589）生三百六十律，以为生律越多，越有可能回到黄钟，结果未能返回黄钟。人们不得不从另一角度思考问题，即从十二律本身内部来调整各律高度，使之能返回黄钟。于是有南朝宋何承天（370—447）的均差律，有隋刘焯（544—610）的等差管律，均因未能从理论上透彻论证“三分损益”不能返回黄钟的缘由，故而也就不能寻找到正确的数学方法去产生新律。朱载堉是第一个以数学方法论证“三分损益”不能返回黄钟的艺术科学家。他指出不能返回黄钟是因为三分损益的生律比值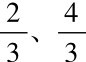自身数量特点所决定。他多次指出：“三分损益往而不返，其弊概由七五为法，法太过而实不及也。”⑬“七五者何？四分尺之三也。实弱法强，往而不返是以疏也。”⑭即分母太大，分子太小不能返回黄钟。他认为不论这样继续生律多少次，三分损益总是不能回到黄钟的。对此他作了如下精彩的数学证明：“苟不因自然之理，而但以三分损益之法衍之，殆不止三百六十，虽至百千万亿，往而不返，终不能合还元之数，况于六十律哉!”⑮这里是命题，接着在下面给予了证明：“然算家以仲吕求黄钟，殚其术而不能合乎十七万七千一百四十七之算。有以倍数四因之者，则三分之不尽二算，而亏数已多；有以正数四因之者，则亦有一算不行，而亏数且过半矣。……”⑯这里是说黄钟律数177147（即311，首见于《淮南子·天文训》，按三分损益其所生得的仲吕律数为131072），若从仲吕律数继续再生律，应乘以得：

131072×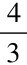=174762……2（余数二，即“不尽二算”）。

四舍五入第一位小数后得174763，与应返回的黄钟律数177147比较就“亏数已多”7○1。若依从《前汉书·律历志》所生仲吕正律65536继续生律，则应得：

65536×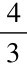=87381……1（余数一，即“亦有一算不行”）。

即所生得的已亏损的律数87381与黄钟半律数88573.5相比较，已低过了黄钟半律数，这就是“亏数且过半矣。”

到此，朱氏是以前十二次生律论证三分损益法不能返回黄钟。随后，则是对十二次之后的生律进行论证。他说：“三分不行之算既未有以处之，记其余分终有不尽之处，持未定之算而谓之黄钟变律，又推以为林钟、太簇、南吕、姑洗、应钟之变。甚者讬名执始，不自信其为黄钟，……”⑱就是说自第十二次生律起，继续生律，“其余分终有不尽之处”，即总是得到无限小数，而黄钟正律、倍律是整数，就是半律或再折半下去的某一再半律也是有限小数，自然与三分损益在十二次后（包括第十二次）生得的律数是无限小数绝不相同。因而，即使生律“虽至百千万亿”次之多，仍然“往而不返，终不能合还元之数”。

朱载堉对三分损益不能返回黄钟的这一证明，完全合于形式逻辑演绎法的任何严格要求。朱氏说：“是故新法不用三分损益，别造密率”⑲是有严格的数学理论根据的。

三、十二平均律等比数列模型的构建与求解

朱载堉在《律吕精义·内篇》中，以数学方法与形式，对十二平均律作了科学的定义，称其为“新法密率”。他写道：“盖十二律黄钟为始，应钟为端，终而复始，循环无端，……是故各律皆以黄钟正数十寸乘之为实，皆以应钟倍数十寸五分九厘四毫六丝三忽○九纤……为法除之，即得其次律也。”⑳这个定义与当今十二平均律的定义没有什么差别，仅仅须将数学用语与符号变换为适合当今的习惯，例如将应钟倍律数改写成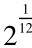的形式即可。这定义是以准确的数学语言，构造了以黄钟律数为首项，以应钟倍律的倒数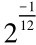（或大吕正律）为公比的十二平均律等比数列。他按定义逐项计算了从黄钟倍律2到应钟半律共三十六项律数，每项计算数值达二十五位数字! 现列出其中的二十五项律数（保留六位小数），以示意朱氏的十二平均律等比数列（见“表一”）。

表一朱载堉十二平均律等比数列

朱氏留下的著作，叙述了他是如何确定构建十二平均律等比数列的充分并且必要条件的。首先，他确定一个八度音程内应是十二律。他说：“……殊不知圣人所以定律止于十二者，取诸自然之理而已。”“天之大数止于十二，故律吕相生其数亦然也。”即是确定了数列在一个八度音程内应为十三项（倍黄与正黄各一项）。其次，他说：“二，本是二尺，进作二百寸为实……”命黄钟倍律为2，而黄钟之长一尺，即设八度音程律长的比值为2。再次，他还多次表述了十二律应是等比的意见，例如他对何承天、刘焯的平均律倾向称：“似亦有见矣。”特别是他以天文历法中的冬至、夏至、春分、秋分的关系比喻黄钟、蕤宾、夹钟、南吕，以阐明蕤宾是黄钟倍律与黄种正律的比例中项，夹钟是黄钟倍律与蕤宾的比例中项，而南吕是蕤宾与黄钟的比例中项，并以详细运算程序的数学语言表达了求解各律的公式，明确地表现了十三项律数为等比数列。这样，他就确立了首项与末项的比值为2，项数为十三的等比数列，并在首项为黄钟倍律2，末项黄钟正律为1的条件下解出了数列的各项。

除上述用求等比中项解十二平均律等比数列各项外，朱氏还在《律吕精义·内篇》卷一《不用三分损益第三》中，将黄钟倍律数2连续两次开平方，然后又开立方，当然这就是将黄钟倍律数2开十二次方。他指出，所得到的2的十二次方根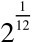，就是应钟倍律数。然后，就如上面所提到的那样，他定义了十二平均律：“各律皆以黄钟正数……为实，皆以应钟倍数……为法除之，即得其次律也”，这样构造性地给出了等比数列的各项。他明确指出：“新法算律与方圆皆用勾股术”，即用我国古算勾股定理进行运算。在第一次开平方时，以 “……二百寸为弦幂，置弦幂为实，开平方法除之得弦一尺四寸……即蕤宾倍律之率，”即是以二百平方寸作正方形面积，开平方得平方根，就是蕤宾倍律数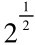。第二次开平方是将蕤宾倍律数“以勾十寸乘之”，转化为正方形面积得“平方积一百四十一寸……为实，开平方法除之得一尺一寸……即南吕倍律之率”，即得2的四次方根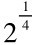。第三次是开立方，他将南吕倍律以“勾十寸乘之，又以股十寸乘之得立方积一千一百八十九立方寸……为实，开立方法除之得一尺〇五分……即应钟倍律之率。”这即是将南吕倍律变换为正立方体体积，开立方求得应钟倍律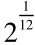，完成了求2的十二次方根的数学工作。

可以认为，朱氏以两种方法解出並构建十二平均律等比数列，是为了从不同角度出发得出结论的一致性来证实结论的正确性。这一工作，使他成为世界上第一位用等比中项解等比数列及第一位用珠算算法完成2的十二次方根达二十五位数字的数学家。

在此，我们不能不为《新格罗夫音乐与音乐家大辞典》所载库特纳（Fritz A. Kuttner）先生关于朱载堉十二平均律的意见感到遗憾。库特纳先生认为：“朱发明的十二平均律的计算方法，并不是通过对2的十二次方根理论的理解和计算，而是用数字学的方法得出了同样的解答。”这里仅就上面我们对朱氏创建十二平均律中的部分数学工作——求等比中项法解等比数列与求2的十二次方根的勾股术方法——的简要介绍，足以证实库特纳先生的意见与朱氏所作工作及论述是完全不相符合的，是违背历史事实的论断。至于说用数字学方法，居然能够准确求出2的十二次方根达二十五位数字，那更是没有任何根据的谈论了。

四、十二平均律等比数列的一个重要性质的论述——两项间项数差求两律间生律率

朱氏在求解、定义十二平均律等比数列模型的基础上，还对多种生律法进行了论述，如“相生四法”、各律自乘应得何律，等等。除“相生四法”中的“其三”法是采用十二平均律定义生律外，其余皆可说是十二平均律等比数列性质的论述。其中，《算学新说》答第十一问所论，从两律项数差求两律间生律率，至为重要，应予重视。

朱氏曾以“隔八、隔六相生之图”○29（如图一），将同一八度中，从黄钟律开始，长生短隔八、短生长隔六的生律顺序所生各律，由长到短排列出来。为此他写道：“律吕相生，或逾五，或逾七。逾五者连本位数则为隔六，逾七者连本位数则为隔八。”此处的两项相“逾”者，即所生律与本位律之间的项数差。两项相“隔”者，即连同所生律到本位律在内的所有项数。

图1 隔八隔六相生之图

图二大吕应钟夹辅之图

朱氏还在《算学新说》第九问中，通过用于旋宫的《大吕应钟夹辅之图》（如图二）的外圈律名，将十二平均律各项顺序与项数差给予了图示。并通过可转动的内圈，将十二平均律的七声音阶各音与宫音的项数差作了图示。

在《算学新说》答第十一问中，他论述了如何由任意一音为宫的律数，去求得音阶中其余各音律数的“相求之率”即生律率。这里以他所述“宫徵相求之率”为例，以见其论述这一问题的一斑。

所谓“宫徵相求之率”即是由宫音右转项数差为七生得徵音的生律率。他写道：“仲吕为宫则黄钟为徵，黄钟为宫则林钟为徵，是故仲吕、林钟二律，名为宫徵相求之率。”因为宫音可以任意旋定，旋宫实际已阐明等比数列的这样一个性质：两律项数差一定，则两律间的生律率也就一定。这里他明确指出：仲吕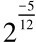律率、林钟律率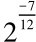，是由宫求徵的相生率。

之后，他穷举了所有十二音为宫时求徵的计算程序。例如他以黄钟为宫，求黄钟之徵时写道：“置黄钟为实以林钟乘之得林钟，或置黄钟为实以仲吕除之亦得林钟，是为黄钟之徵。”又如他以大吕为宫，求大吕之徵时写道：“置大吕为实，以林钟乘之得夷则，或置大吕为实以仲吕除之亦得夷则，是为大吕之徵。”如果将“宫徵相求”的十二条文用今日数学形式表示，可概括为：(www.xing528.com)

为宫律率n×林钟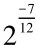律率=为徵律率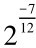n……（1）'

为宫律率n÷仲吕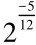律率=为徵律率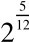n……（2）'

以上二式，所得为徵律率仅是八度的差别，运用他所讲“所得多则半之，少则倍之”的原则，所得律数可化为相同。

朱氏以上面的方式论述了由宫某律求七声音阶中其余六声的全部“相求之率”与各律。虽然他未对七声音阶之外的各律再一一阐述其“相求之率”，但其论述过程已经表明他无疑掌握了由任意两律项数差求两项间相生律这一等比数列的重要性质。

这一性质与朱氏其他生律方法有密切关系，这里仅以“相生四法”中的“其一”法为例作一说明。朱氏在“其一”法中写道：“其一，黄钟生林钟，林钟生太簇，……仲吕生黄钟。长生短，五亿乘之，短生长，十亿乘之，皆以七亿四千九百一十五万三千五百三十八除之。”将这段话用今日数学式写出，即是：

长生短隔八；

短生长隔六；

两相对照，“其一”法的生律公式（1）'、（2）'与前面所列“宫徵相求”公式（1）、（2）所表达的内容全然相同，这就告诉我们，“隔八、隔六相生”的“其一”法，实是连续运用“宫徵相求”的结果。

若是对“相生四法”中的“其四”法，也作如上剖析，不难明白实是连续运用“宫和相求”的结果。

可以说十二平均律的任何相生之法，都可以从项数差确定生律率这一性质中找到相应的生律根据。朱氏正是以这一重要性质，掌握各生律法并以多种形式构建十二平均律的。可以说在朱氏定义了十二平均律之后，这一性质实际上揭示了十二平均律各种生律法之间、各构建法之间的等价关系。朱载堉以他的等比数列理论及运用数学理论的娴熟技巧，出色地做到了“十二律吕，参伍以变，错综其数，交互相求，反复皆得。”○30

五、结束语

朱载堉对十二平均律等比数列的论述，所给定义确切、严密，运用概念准确、合理，论断合乎逻辑，完全具备数学理论的特点与要求。限于篇幅，这里不能讨论他的更广泛的数学工作及所建立的数学理论，例如他的珠算开平方、开立方的算法程序化，等等。但是不能忘记，如果不是在所有这些数学方法与理论上的创见，十二平均律所遇到的艰辛工作是万难完成的。那种以为他的数学工作仅是“数学演算”的看法，即使是出于对他的工作缺乏了解，也不能不说是错误的看法。

中国古代数学有着光辉的成就，在世界科学文化史上有着崇高的地位，为人类文明与进步作出了巨大贡献。中国古代数学未采用公理化方法体系。但没有采用公理化方法并不等于没有归纳出公理或没有运用公理，更不等于没有逻辑推断与数学思维，不等同于没有数学理论。我国古代数学是以问题为出发点，以解决问题为主旨，以构造性程序化和精于计算见长为其特色的算法体系。计算本身就含有推证，就要运用公理、假设、前提、定理、公式以达到正确的结论。朱载堉的数学理论正是保持了中国古代数学这一特点，并使得他完成了中华音乐文化史上近两千年追求旋宫的审美理想，同时也使他毫无愧色地第一个登上在世界音乐文化史上创建十二平均律的这一高峰。他所创建的数学理论，关于音、律、数、度、理的闪烁着辩证唯物主义光辉的哲理以及他为追求真理所表现出来的献身精神，永远值得我们学习和纪念。