网络计划基本概念与识读 ─ 专业施工管理实战指南

（一）网络计划的概念及基本原理

网络计划是以网络图的形式来表达任务构成、工作顺序并加注工作时间参数的一种进度计划。网络图是指由箭线和节点（圆圈)组成的，用来表示工作流程的有向、有序的网状图形。网络图按其所用符号的意义不同，可分为双代号网络图和单代号网络图两种。

网络计划方法的基本原理是：首先，绘制工程施工网络图，以此来表达计划中各施工过程先后顺序的逻辑关系；其次，通过计算，分析各施工过程在网络图中的地位，找出关键线路及关键施工过程；再次，按选定目标不断改善计划安排，选择最优方案，并付诸实施；最后，在执行过程中进行有效的控制和监督，使计划尽可能地实现预期目标。

（二）网络计划分类

网络计划是一种内容非常丰富的计划管理方法，在实际应用中，通常从不同角度将其分成不同的类别。比较常见的分类方法有以下几种：

1.按工作表示方法的不同分类。

（1)双代号网络计划。

双代号网络计划是各项工作以双代号表示法绘制而成的网络计划。在网络图中，以箭线代表工作，节点表示过程开始或结束的瞬间，计划中的每项工作均可用箭线两端的节点内的编号来表示。

（2)单代号网络计划。

单代号网络计划是以单代号的表示方法绘制而成的网络计划。在单代号网络图中，以节点表示工作，箭线仅表示过程之间的逻辑关系，并且，各工作均可用该工作节点中的编号来表示。

2.按有无时间坐标分类。

（1)无时标网络计划。

不带有时间坐标的网络计划称为无时标网络计划。在无时标网络计划中，工作箭线长度与该工作的持续时间无关，各施工过程持续时间用数字写在箭线的下方，习惯上简称网络计划。

（2)有时标网络计划。

带有时间坐标的网络计划称为有时标网络计划。该计划以横坐标为时间坐标，每项工作的时间坐标的时间单位可根据实际需要来确定。

（三）双代号网络图的构成

双代号网络图的基本构成有箭线、节点、节点编号和线路，通常箭线、节点和线路成为双代号网络图组成的三要素。

1.箭线。

网络图中一端带箭头的线称为箭线。在双代号网络图中，它与其两端的节点共同表示一项工作。箭线的形式与对应的含义有以下几种情况：

（1)实箭线与其两端的节点构成的工作，表示实际发生的工作，即实工作。在双代号网络图中，实工作有两种情况：

①既消耗时间又消耗资源的工作，它是在网络计划中必须要发生的工作，如装饰抹灰。

②只消耗时间而不消耗资源的工作，它在网络计划中也是必须要发生的工作，如装饰抹灰中的砂浆找平层的干燥时间，如果单独作为一个施工过程来对待，它也应该要发生的，因此要作为一个实实在在的工作来对待。

（2)虚箭线与其两端的节点构成的工作，表示虚拟发生的工作，即称为虚工作。在网络图中，虚箭线仅表示工作之间的逻辑关系，不消耗任何时间和资源。

2.节点。

节点表示工作之间的联结。在时间上，它表示一个工作的开始（结束)或另一个工作的结束（开始)，这意味着前后工作交接的瞬间。箭线的出发节点叫作该工作的开始节点，箭头指向的节点叫该工作的结束节点。任何工作都可以用箭线和其前、后的两个节点来表示，起点节点编号在前，终点节点编号在后。网络图的第一个节点称为整个网络图的起始节点，最后一个节点称为网络图的终点节点，其余的节点均称为中间节点。起点节点是网络图的第一个节点，表示一项任务的开始。终点节点是网络图的最后一个节点，表示一项任务的完成。除起点节点和终点节点外的中间节点都有双重的含义，既是前面工作的结束节点，也是后面工作的开始节点。

3.节点编号。

网络图中的每个节点都有自己的编号，以便赋予每项工作以代号。节点编号一般有以下的基本规则。

（1)箭头节点编号大于箭尾节点编号。

（2)在一个网络图中，所有节点不能出现重复编号。

（3)编号的号码可以按连续编号，也可以按非连续编号。

4.线路。

从起始节点开始，沿着箭线方向直至终点节点，中间经由一系列节点和箭线，由此所构成的若干条“通道”，称为线路。一个网络图中，从起始节点到终点节点，一般都存在着许多条线路，每条线路上都包含若干项工作，这些工作的持续时间之和就是该线路的时间长度，即完成线路上所有工作所需花费的时间。在网络图的所有线路中，持续时间最长的线路被称为关键线路，它表示完成网络计划中所有工作所需花费的最短时间。网络计划中，关键线路可能不止一条，关键线路条数的多少由持续时间最长线路的个数决定。位于关键线路上的工作称为关键工作，除关键工作以外的其他工作称为非关键工作。关键线路通常采用粗箭线、双箭线或彩色线来表示，以表示突出。在实际工作中，关键线路也不是一成不变的，在一定的条件下，关键线路和非关键线路会相互转化，例如，当采取技术组织措施，缩短关键工作的持续时间，或者延长非关键工作持续时间时，就有可能使关键线路发生改变。

（四）双代号网络图的绘制

正确绘制工程的网络图是网络计划方法应用的基础。因此，正确绘制网络图一方面必须正确表达工作之间的各种逻辑关系；另一方面必须遵守双代号网络图绘制的基本规则。也就是说：一个正确的双代号网络图应是在遵守绘图规则的基础上，正确表达工作之间的逻辑关系的一个网络图。此外，绘制工程的网络图时，还应选择适当的排列方法。

1.网络图逻辑关系。

网络图中的逻辑关系是指网络图中所表示的各个工作之间客观上存在或主观上安排的先后顺序关系。这种顺序关系划分为两类：一类是施工工艺关系，简称工艺逻辑；另一类是施工组织关系，简称组织逻辑。工艺逻辑关系是由施工工艺或操作规程所决定的各个工作之间客观上存在的先后施工顺序。对于一个具体的分部工程来说，当确定了施工方法以后，该分部工程的各个工作的先后顺序一般是固定的，不能颠倒。组织逻辑关系是施工组织安排中，考虑劳动力、机具、材料或工期等影响，在各工作之间主观上安排的先后顺序关系。这种关系不受施工工艺的限制，不是工程性质本身决定的，而是在保证施工质量、安全和工期等前提下，人为安排的顺序关系。

逻辑关系表达是否正确，是网络图能否正确反映工程实际情况的关键，错误的逻辑关系将使各项工作的时间参数、关键线路和工程工期发生错误，就不能正确反映工程客观实际情况。

2.网络图绘制的基本规则。

网络图在绘制过程中，除正确表示逻辑关系外，还要遵循一定的绘图规则：

（1)网络图中应只有一个起点节点和一个终点节点。

（2)除网络图的起点节点和终点节点外，不允许出现没有外向箭线的节点和没有内向箭线的节点。

（3)网络图中严禁出现从一个节点出发，顺箭头方向又回到原出发点，即出现循环回路。

（4)在网络图中严禁出现用相同的编号表示不同的工作。

（5)网络图中严禁出现没有箭尾节点的箭线或没有箭头节点的箭线。

（6)网络图中严禁出现无指向箭头或有双向箭头的连线。

（7)应尽量避免网络图中工作箭线的交叉。当交叉不可避免时，可以采用过桥法或指向法处理。

（8)双代号网络图中的箭线（包括虚箭线)宜保持自左向右的方向，不宜出现箭头指向左方的水平箭线和箭头偏向左方的斜向箭线。

（9)双代号网络图中，一项工作只有唯一的一条箭线和相应的一对节点编号。严禁在箭线上引入或引出箭线。

（10)在双代号网络图中某些节点有多条外向箭线或多条内向箭线时，在保证一项工作有唯一的一条箭线和对应的一对节点编号前提下，允许使用母线绘制。

3.双代号网络图的绘制步骤和要求。

（1)绘制步骤。

①绘制网络图之前，首先收集整理有关该网络计划的资料。

②根据工作之间的逻辑关系和绘图规则，从起始节点开始，从左到右依次绘制网络计划的草图。

③检查各工作之间的逻辑关系是否正确，网络图的绘制是否符合绘图规则。

④整理、完善网络图，使网络图条理清楚、层次分明。

⑤对网络图各节点进行编号。

（2)绘制要求。

①网络图的箭线应以水平线为主，竖线和斜线为辅，不应画成曲线。②在网络图中，箭线应保持自左向右的方向，尽量避免“反向箭线”。③在网络图中应正确应用虚箭线，力求减少不必要的虚箭线。

例3.1 已知网络图的资料见表3.1，试绘制双代号网络图。

表3.1 网络图中各工作之间的逻辑关系表

解：绘制网络图，如图3.2所示。

图3.2 双代号网络图

（五）双代号网络图时间参数的计算

网络计划时间参数的计算是确定关键工作、关键线路和计算工期的基础，是对网络计划进行有目的地调整、优化的主要依据。双代号网络计划时间参数主要包括节点最早时间、节点最迟时间、工作最早可能开始和完成时间、工作最迟必须开始和完成时间、工作总时差和自由时差以及计算工期等。时间参数的计算方法主要分为工作计算法和节点计算法两种。每一种方法又可以分为公式计算法（也叫分析法)、图上计算法、矩阵法和电算法等，这里只介绍公式计算法。

1.时间参数表示的常用符号。

设有线路○h→○i→○j→○k，则：

Di-j——工作i-j的持续时间；

ETi——i节点的最早时间；

LTi——i节点的最迟时间；

ESi-j——i-j工作的最早开始时间；

LSi-j——i-j工作的最迟开始时间；

EFi-j——i-j工作的最早完成时间；

LFi-j——i-j工作的最迟完成时间；

TFi-j——i-j工作的总时差；

FFi-j——i-j工作的自由时差。

2.工作的时间参数计算。

常用的双代号网络计划工作的时间参数标注的形式通常采用六时参数标注法。

公式计算法计算时间参数的步骤如下：

（1)计算工作的最早开始时间（ESi-j)。

工作最早开始时间亦称工作最早可能开始时间。它是指各紧前工作全都完成，具备了本工作开始的必要条件的最早时刻。

①计算顺序。

由于最早开始时间是以紧前工作的最早开始或最早完成时间为依据，所以，它的计算必须在各紧前工作都计算后才能进行。因此该种参数的计算，必须从网络图的起点节点开始，顺箭线方向逐项进行，直到终点节点为止。

②计算方法。

凡与起点节点相连的工作（平行工作)都是计划的起始工作，当未规定其最早开始时间ESi-j时，其值都定为零。即ESi-j=0（i=1)

所有其他工作的最早开始时间的计算方法是：将其所有紧前工作h-i的最早开始时间ESh-i分别与各工作的持续时间相加，取和数中的最大值；或取各紧前工作最早完成时间的最大值。如下式：

ESi-j=max｛ESh-i+｝

式中，ESh-i——工作i-j的紧前工作h-i的最早开始时间；Dh-i——工作i-j的紧前工作h-i的持续时间。

（2)计算工作的最早完成时间（EFi-j)。

工作最早完成时间亦称工作最早可能完成时间。它是指一项工作如果按最早开始时间开始的情况下，该工作可能完成的最早时刻。工作i-j的最早完成时间用EFi-j表示，其值等于该工作最早开始时间与其持续时间之和。工作的最早完成时间的计算应从网络计划的起始节点开始，顺着箭线方向依次进行，计算公式如下：

EFi-j=ESi-j+Di-j

在采用六时参数标注法时，某项工作的最早开始时间计算后，应立即将其最早完成时间计算出来，以便于其紧后工作的计算。

（3)确定网络计划的工期。

网络计划的工期泛指完成工程任务所需的时间，分为计算工期、要求工期和计划工期三种。

①计算工期是指根据网络计划时间参数计算而得到的工期，用Tc表示。计算公式：

Tc=max｛EFi-n｝

式中，EFi-n——以终点节点（j=n)为箭头节点的工作i-n的最早完成时间。

②要求工期是指合同规定或业主要求、企业上级要求的工期，用Tr表示。

③计划工期是指完成网络计划的工作所计划（打算)工期，用Tp表示。

当规定了要求工期时，计划工期不应超过要求工期，即：

Tp≤Tr

当未规定要求工期时，可令计划工期等于计算工期，即：

Tp=Tr

（4)计算工作的最迟完成时间LFi-j。

工作最迟完成时间是指在不影响整个任务按期完成的前提下，工作必须完成的最迟时刻。工作最迟完成时间和工作最迟开始时间的计算应从网络计划的终点节点开始，逆着箭线方向依次进行。其计算步骤如下。

第一步：以网络计划终点节点为完成节点的工作，其最迟完成时间等于网络计划的计划工期，即：

LFi-n=Tp

式中，LFi-n——以网络计划终点节点n为完成节点工作的最迟完成时间。

第二步：其他工作的最迟完成时间应等于其紧后工作最迟开始时间的最小值，即：

LFi-j=min｛LFj-k-Dj-k｝=min｛LSj-k｝

式中，LSj-k——工作i-j的紧后工作j-k的最迟开始时间；LFj-k——工作i-j的紧后工作j-k的最迟完成时间；Dj-k——工作i-j的紧后工作j-k的持续时间。(www.xing528.com)

（5)计算工作的最迟开始时间LSi-j。

工作的最迟开始时间亦称最迟必须开始时间。它是在保证工作按最迟完成时间完成的条件下，该工作必须开始的最迟时刻。工作的最迟开始时间的计算应从网络计划的终点节点开始，逆着箭线方向依次进行。其计算步骤如下：

LSi-j=LFi-j-Di-j=min｛LSj-k｝-Di-j

（6)计算工作的总时差TFi-j。

工作总时差是指在不影响总工期的前提下，一项工作所拥有机动时间的最大值。它等于本工作最早开始时间到最迟完成时间这段极限活动范围，再扣除工作本身必需的持续时间所剩余的差值。用公式表达如下：

TFi-j=LSi-j-ESi-j=LFi-j-EFi-j

（7)计算工作的自由时差FFi-j。

自由时差是指一项工作在不影响其紧后工作最早开始的前提下，可以灵活使用的机动时间。它等于本工作最早开始时间到紧后工作最早开始时间这段极限活动范围，再扣除工作本身必需的持续时间所剩余的差值的最小值。用公式表达如下：

FFi-j=min｛ESi-j-EFi-j｝=min｛ESi-j-ESi-j-Di-j｝

式中，ESj-k——工作i-j的紧后工作j-k的最早开始时间。

采用六参数法计算时，用紧后工作的最早开始时间的最小值减本工作的最早完成时间即可。对于网络计划的结束工作，应将计算工期看作紧后工作的最早开始时间进行计算。对于无紧后工作的工作，也就是以网络计划终点节点为完成节点的工作，其自由时差等于计划工期与本工作最早完成时间之差，即：

FFi-n=TP-EFi-n

式中，FFi-n——以网络计划终点节点n为完成节点的工作i-n的自由时差；EFi-n——以网络计划终点节点n为完成节点的工作i-n的最早开始时间。

（8)确定关键工作和关键线路。

在网络计划中，总时差最小的工作为关键工作。当网络计划的计划工期等于计算工期时，总时差为零的工作就是关键工作。

从起点节点到终点节点全部由关键工作组成的线路为关键线路，一般用粗线、双线箭线或彩色箭线标出。

3.节点的时间参数计算。

公式法计算节点的时间参数和时差。

每个节点有两个时间参数：节点最早时间和最迟时间，分别用ETi和LTi表示。

（1)节点的最早时间ETi。

节点i的最早时间ETi是指以计划起点节点的时间ETi=0相对于这个时间，顺着箭线方向到达每一个节点的时刻，它表示以该节点为结束节点的各项工作全部完成，并以这个节点为开始节点的紧后工作最早可能开始的时间。节点最早时间的计算应从网络计划的起点节点开始，顺着箭线方向依次进行。其计算步骤如下：

①网络计划的起点节点，如未规定最早时间时，其值等于零。

②其他节点的最早时间应按公式进行计算：ETj=max｛ETi+Di-j｝。

③网络计划的计算工期等于网络计划终点节点的最早时间，即：Tc=ETn。（网络计划终点节点n的最早时间)

（2)节点的最迟时间LTi。

节点i的最迟时间LTi是指在计划工期Tp确定的情况下，以计划工期作为网络图终点节点的最迟时间，逆箭线方向依次逐项计算。它表示以该节点为开始节点的各项工作最迟必须开始的时间，也就是说以该节点为结束节点的各项工作最迟在这个时间必须全部完成，否则必将延误总工期。其计算步骤如下：

①网络计划终点节点的最迟时间等于网络计划的计划工期，即：LTn=Tp。

②其他节点的最迟时间应按公式进行计算：LTi=min｛LTj-Di-j｝。

（3)节点时间参数与工作总时差的关系。

根据总时差的含义以及节点时间参数与工序时间参数的关系，用两个节点时间参数表示工作总时差的公式为：

TFi-j=LTj-LTi

（4)节点时间参数与工作自由时差的关系。

根据自由时差的含义以及节点时间参数与工序时间参数的关系，用两个节点时间参数表达工作自由时差的公式为：

FFi-j=ETj-ETi-Di-j

4.关键节点的特性。

在双代号网络计划中，当计划工期等于计算工期时，关键节点具有以下一些特性，掌握好这些特性，有助于确定工作的时间参数。

（1)开始节点和完成节点均为关键节点的工作，不一定是关键工作。

（2)以关键节点为完成节点的工作，其总时差和自由时差必然相等。

（3)当两个关键节点间有多项工作，且工作间的非关键节点无其他内向箭线和外向箭线时，则两个关键节点间各项工作的总时差均相等。在这些工作中，除以关键节点为完成的节点的工作自由时差等于总时差外，其余工作的自由时差均为零。

（4)当两个关键节点间有多项工作，且工作间的非关键节点有外向箭线而无其他内向箭线时，则两个关键节点间各项工作的总时差不一定相等。在这些工作中，除以关键节点为完成的节点的工作自由时差等于总时差外，其余工作的自由时差均为零。

5.节点标号法确定关键线路和计算工期。

标号法是一种快速寻求网络计算工期和关键线路的方法。它利用按节点计算法的基本原理，对网络计划中的每一个节点进行标号，然后利用标号值确定网络计划的计算工期和关键线路。现以图3.3为例说明节点标号法确定关键线路的具体步骤。

（1)设网络计划起点节点的标号值为零，即b1=0。

（2)顺箭线方向逐个计算其他节点的标号值。每个节点的标号值，等于以该节点为完成节点的各工作的开始节点标号值与相应工作持续时间之和的最大值，即：

bj=max｛bi+Di-j｝

图3.3 双代号网络计划(标号法)

图3.3中，节点③和节点④的标号值分别为：

b3=b1+D1-3=0+4=4

b4=max｛b1+D1-4，b3+D3-4｝

=max｛0+2，4+0｝=4

当计算出节点的标号值后，应该用其标号值及其源节点对该节点进行双标号。所谓源节点，就是用来确定本节点标号值的节点。如果源节点有多个，应将所有源节点标出。例如在图3.3中，节点④的标号值4是由节点③所确定，故节点④的源节点就是节点③。

（3)节点标号完成后，终点节点的标号值即为网络计划的计算工期。在图3.3中，其计算工期就等于终点节点⑦的标号值15。

（4)从网络计划终点节点开始，逆箭线方向按源节点寻求出关键线路。例如在本例中，从终点节点⑦开始，逆着箭线方向按源节点可以找出关键线路为①→③→④→⑥→⑦。计算结果如图3.4所示。

图3.4 双代号网络计划(标号法)

（六）单代号网络计划

单代号网络图是以节点及其编号表示工作，以箭线表示工作之间逻辑关系的网络图，并在节点中加注工作代号、名称和持续时间，以形成单代号网络计划。

1.单代号网络图的特点。

单代号网络图与双代号网络图相比，具有以下特点：

（1)工作之间的逻辑关系容易表达，且不用虚箭线，故绘图较简单。

（2)网络图便于检查和修改。

（3)由于工作持续时间表示在节点之中，没有长度，故不够形象直观。

（4)表示工作之间逻辑关系的箭线可能产生较多的纵横交叉现象。

2.单代号网络图的基本符号。

（1)节点。

单代号网络图中的每一个节点表示一项工作，节点宜用圆圈或矩形表示。节点所表示的工作名称、持续时间和工作代号等应标注在节点内单代号网络图中的节点必须编号。编号标注在节点内，其号码可间断，但严禁重复。箭线的箭尾节点编号应小于箭头节点的编号。一项工作必须有唯一的一个节点及相应的一个号。

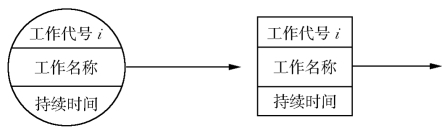
图3.5 单代号网络图工作的表示方法

（2)箭线。

单代号网络图中的箭线表示紧邻工作之间的逻辑关系，既不占用时间，也不消耗资源。箭线应画成水平直线、折线或斜线。箭线水平投影的方向应自左向右，表示工作的行进方向。工作之间的逻辑关系包括工艺关系和组织关系，在网络图中均表现为工作之间的先后顺序。

（3)线路。

单代号网络图中，各条线路应用该线路上的节点编号从小到大依次表述。

3.单代号网络图的绘图规则。

（1)单代号网络图必须正确表达已定的逻辑关系。

（2)单代号网络图中，严禁出现循环回路。

（3)单代号网络图中，严禁出现双向箭头或无箭头的连线。

（4)单代号网络图中，严禁出现没有箭尾节点的箭线和没有箭头节点的箭线。

（5)绘制网络图时，箭线不宜交叉，当交叉不可避免时，可采用过桥法或指向法绘制。

（6)单代号网络图中只应有一个起点节点和一个终点节点。当网络图中有多项起点节点或多项终点节点时，应在网络图的两端分别设置一项虚工作，作为该网络图的起点节点（St)和终点节点（Fin)。

单代号网络图的绘图规则大部分与双代号网络图的绘图规则相同，故不再进行解释。

4.单代号网络计划时间参数的计算。

单代号网络计划时间参数的计算应在确定各项工作的持续时间之后进行。时间参数的计算顺序和计算方法基本上与双代号网络计划时间参数的计算相同。

（七）双代号时标网络计划

1.双代号时标网络计划的定义。

双代号时标网络计划是以时间坐标为尺度编制的网络计划。时标网络计划中应以实箭线表示工作，以虚箭线表示虚工作，以波形线表示工作的自由时差。

2.双代号时标网络计划的特点。

双代号时标网络计划是以水平时间坐标为尺度编制的双代号网络计划，其主要特点如下：

时标网络计划兼有网络计划与横道计划的优点，它能够清楚地表明计划的时间进程，使用方便；

时标网络计划能在图上直接显示出各项工作的开始与完成时间，工作的自由时差及关键线路；

在时标网络计划中可以统计每一个单位时间对资源的需要量，以便进行资源优化和调整；

由于箭线受到时间坐标的限制，当情况发生变化时，对网络计划的修改比较麻烦，往往要重新绘图。但在使用计算机以后，这一问题已较容易解决。

3.双代号时标网络计划的一般规定。

（1)双代号时标网络计划必须以水平时间坐标为尺度表示工作时间。时标的时间单位应根据需要在编制网络计划之前确定，可为时、天、周、月或季。

（2)时标网络计划应以实箭线表示工作，以虚箭线表示虚工作，以波形线表示工作的自由时差。

（3)时标网络计划中所有符号在时间坐标上的水平投影位置，都必须与其时间参数相对应。节点中心必须对准相应的时标位置。

（4)时标网络计划中虚工作必须以垂直方向的虚箭线表示，有自由时差时加波形线表示。

4.双代号时标网络计划的编制。

时标网络计划宜按各个工作的最早开始时间编制。在编制时标网络计划之前，应先按已确定的时间单位绘制出时标计划表（表3.2)。

表3.2 时标计划表

双代号时标网络计划的编制方法有两种。

（1)间接法绘制。

先绘制出时标网络计划，计算各工作的最早时间参数，再根据最早时间参数在时标计划表上确定节点位置，连线完成，某些工作箭线长度不足以到达该工作的完成节点时，用波形线补足。

（2)直接法绘制。

根据网络计划中工作之间的逻辑关系及各工作的持续时间，直接在时标计划表上绘制时标网络计划。绘制步骤如下。

将起点节点定位在时标表的起始刻度线上。

按工作持续时间在时标计划表上绘制起点节点的外向箭线。

其他工作的开始节点必须在其所有紧前工作都绘出以后，定位在这些紧前工作最早完成时间最大值的时间刻度上，某些工作的箭线长度不足以到达该节点时，用波形线补足，箭头画在波形线与节点连接处。

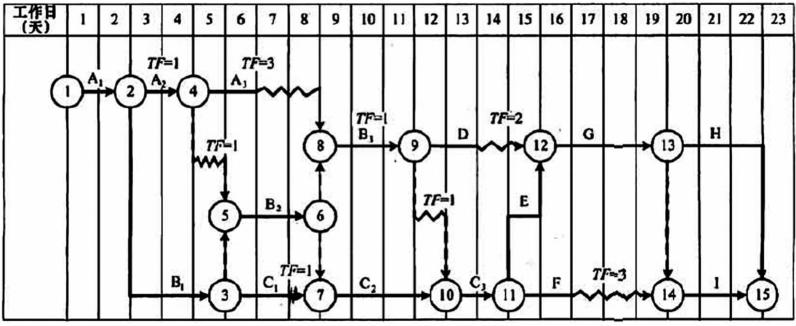
图3.6 时标网络计划示例