【摘要】:众所周知,动力问题通过达兰贝尔原理可以转化为静力问题。我们有理由认为,一切动力系统的变分问题只不过是奥斯特罗德茨基—哈米顿原理之引申。因此下述两个变分原理[1][2]引用奥—哈原理证明,就更为简捷。假定受压柱在振动过程中振幅很小,这样,在其振动中某一瞬时之位能为:图1体系在振动中某一瞬时之动能为:由奥—哈原理得:所以α可以表示为:αmin相应右式的最小值,下面证明上式与精确理论相合。
众所周知,动力问题通过达兰贝尔原理可以转化为静力问题。因此,动力系统的极值问题就能转化为静力系统的变分问题。我们有理由认为,一切动力系统的变分问题只不过是奥斯特罗德茨基—哈米顿原理之引申。因此下述两个变分原理[1][2]引用奥—哈原理证明,就更为简捷。
(一)弹性体系固有频率的变分式
令 为弹性体系单位体积的应变能
为弹性体系单位体积的应变能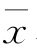

 为弹性体边界上单位面积的约束分量,u、v、w表示三向位移,容易说明体系的总位能为:
为弹性体边界上单位面积的约束分量,u、v、w表示三向位移,容易说明体系的总位能为:
体系的总动能为:
由奥—哈原理:
将①、②式代入③得:
[1] 关于弹性体系固有频率的两个变分原理.胡海昌.
[2] 弹性系统动力稳定理论中的一个变分原理.胡海昌.
对于微幅振动体系存在下列关系:
将⑤式代入④式:
所以体系的固有频率可以表示为:
体系的基本固有频率相应上式的最小值。
(二)变截面杆的动力稳定(https://www.xing528.com)
考虑图1变截面柱,一端固定而另一端铰支且受动力荷载p=p0+αpt作用。假定受压柱在振动过程中振幅很小,这样,在其振动中某一瞬时之位能为:
图1
体系在振动中某一瞬时之动能为:
由奥—哈原理得:
所以α可以表示为:
αmin相应右式的最小值,下面证明上式与精确理论相合。
利用部分积分:
将


 式代入⑨式得:
式代入⑨式得:
上式合并整理:
考虑δw的任意性,由上式可得:
这就是变截面杆的动力稳定方程。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




