二项式定理及常数项的求解

二项式定理可以用以下公式表示:称为二项式系数,即取的组合数目,此系数亦可表示为杨辉三角．

方法简述

例1　求(x＋a)12的展开式中的倒数第4项．

点拨　展开式基本应用

解答　(x＋a)12的展开式中共13项,它的倒数第4项是第10项,

反思　注意是倒数第4项．

例2　(1)求(1＋2x)7的展开式的第4项的系数;

(2)求的展开式中x3的系数及二项式系数．

点拨　展开公式基本应用．

解答　(1＋2x)7的展开式的第4项是

∴(1＋2x)7的展开式的第4项的系数是280．

(2)∵的展开式的通项是

∴9－2r＝3,r＝3．

∴x3的系数(－1)3＝－84,x3的二项式系数＝84．

反思　注意项的系数与二项式系数的区别．

例3　求(x2＋3x－4)4的展开式中x的系数．

点拨　要把上式展开,必须先把三项中的某两项结合起来,看成一项,才可以用二项式定理展开,然后再用一次二项式定理,也可以先把三项式分解成两个二项式的积,再用二项式定理展开．

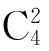解答　解法一:(x2＋3x－4)4＝[(x2＋3x)－4]4＝(x2＋3x)4－(x2＋3x)3×4＋(x2＋3x)2×42－(x2＋3x)×43＋×44,显然,上式中只有第4项中有含x的项,

∴展开式中含x的项的系数是－×3×43＝－768．

解法二:(x2＋3x－4)4＝[(x－1)(x＋4)]4＝(x－1)4(x＋4)4＝

∴展开式中含x的项的系数是

反思　如何体现展开式中x的系数是本题难点．

例4　已知f(x)＝(1＋2x)m＋(1＋4x)n(m,n∈N∗)的展开式中含x项的系数为36,求展开式中含x2项的系数最小值．

点拨　展开式中含x2项的系数是关于m,n的关系式,由展开式中含x项的系数为36,可得2m＋4n＝36,从而转化为关于m或n的二次函数求解．

解答　(1＋2x)m＋(1＋4x)n展开式中含x的项为

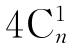×2x＋×4x＝(＋)x,

∴＝36,即m＋2n＝18．

(1＋2x)m＋(1＋4x)n展开式中含x2的项的系数为

t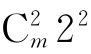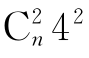＝＋＝2m2－2m＋8n2－8n．

∵m＋2n＝18,∴m＝18－2n．

∴t＝2(18－2n)2－2(18－2n)＋8n2－8n＝16n2－148n＋612＝．

∴当n＝时,t取最小值,但n∈N∗,

∴n＝5时,t(即x2项的系数)最小,最小值为272,此时n＝5,m＝8．

反思　通过含x项的系数为36,求出m,n的关系,进而求得最小值．

易错解读

例5　已知(1－2x)7＝a0＋a1x＋a2x2＋…＋a7x7,求:

(1)a1＋a2＋…＋a7;(2)a1＋a3＋a5＋a7;(3)|a0|＋|a1|＋…＋|a7|．

解答　(1)当x＝1时,(1－2x)7＝(1－2)7＝－1,展开式右边为(www.xing528.com)

a0＋a1＋a2＋…＋a7．

∴a0＋a1＋a2＋…＋a7＝－1．

当x＝0时,a0＝1,∴a1＋a2＋…＋a7＝－1－1＝－2．

(2)令x＝1,a0＋a1＋a2＋…＋a7＝－1．　①

令x＝－1,a0－a1＋a2－a3＋a4－a5＋a6－a7＝37．　②

①－②,得2(a1＋a3＋a5＋a7)＝－1－37．∴a1＋a3＋a5＋a7＝．

(3)由展开式知,a1,a3,a5,a7均为负,a0,a2,a4,a8均为正．

∴由(2)中①＋②,得2(a0＋a2＋a4＋a6)＝－1＋37．

∴a0＋a2＋a4＋a6＝．

∴|a0|＋|a1|＋…＋|a7|＝a0－a1＋a2－a3＋a4－a5＋a6－a7．＝(a0＋a2＋a4＋a6)－(a1＋a3＋a5＋a7)＝37．

易错点　通过赋值法,找到本题的突破口．

例6　已知的展开式中,第五项与第三项的二项式系数之比为14∶3,求展开式的常数项．

解答　依题意

设第r＋1项为常数项,又

令

∴．因此所求常数项为180．

易错点　注意二项式系数与项的系数的区别．

例7　设(1＋x)＋(1＋x)2＋(1＋x)3＋…＋(1＋x)n＝a0＋a1x＋a2x2＋…＋anxn,当a0＋a1＋a2＋…＋an＝254时,求n的值．

解答　令x＝1,得a0＋a1＋a2＋…＋an＝2＋22＋23＋…＋2n＝＝254,∴2n＝128,n＝7．

易错点　对于f(x)＝a0(x－a)n＋a1(x－a)n－1＋…＋an,令x－a＝1,即x＝a＋1可得各项系数的和a0＋a1＋a2＋…＋an的值;令x－a＝－1,即x＝a－1,可得奇数项系数和与偶数项系数和的关系．

1．

经典训练展开式中x4的系数为________,各项系数之和为________．

2．多项式的展开式中,x6的系数为_________．

3．若二项式)的展开式中含有常数项,则n的最小值为(　)．

A．4　B．5　C．6　D．8

4．某企业欲实现在今后10年内年产值翻一番的目标,那么该企业年产值的年平均增长率最低应(　)．

A．低于5%　B．在5%~6%之间

C．在6%~8%之间　D．在8%以上

5．在(1＋x)n的展开式中,奇数项之和为p,偶数项之和为q,则(1－x2)n等于(　)．

A．0　B．pq　C．p2＋q2　D．p2－q2

6．求和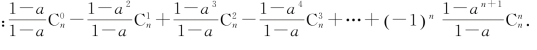

7．求(2＋x)10的展开式中系数最大的项．

8．已知(a2＋1)n展开式中的各项系数的和等于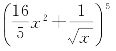的展开式的常数项,而(a2＋1)n展开式的系数的最大的项等于54,求a的值(a∈R)．

9．设(1－x)5 (3＋2x)9＝a0(x＋1)14＋a1(x＋1)13＋…＋a13(x＋1)＋a14．求:

(1)a0＋a1＋…＋a14;

(2)a1＋a3＋…＋a13．

10．求值