正态分布的标准化变换及计算方法简述

由于一般的正态总体其图象不一定关于y轴对称,对于任一正态总体,其取值小于x的概率,只要会用它求正态总体在某个特定区间的概率即可．为了便于描述和应用,常将正态变量作数据转换．将一般正态分布转化成标准正态分布．若

服从标准正态分布,通过查标准正态分布表就可以直接计算出原正态分布的概率值．故该变换被称为标准化变换．

方法简述

例1　设有一正态总体,它的概率密度曲线是函数f(x)的图象,且,则这个正态总体的平均数与标准差分别是(　)．

A．10与8　B．10与2　C．8与10　D．2与10

点拨　由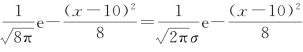,可知σ＝2,μ＝10．故选B．

解答　B

反思　直接运用公式即可．

例2　已知随机变量X服从正态分布N(2,σ2),且P(X＜4)＝0．8,则P(0＜X＜2)等于(　)．

A．0．6　B．0．4　C．0．3　D．0．2

点拨　由P(X＜4)＝0．8知P(X≥4)＝P(X≤0)＝0．2,

故P(0＜X＜2)＝0．3．故选C．

解答　C

例3　已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)＝0．6826,则P(X＞4)等于(　)．

A．0．1588　B．0．1587　C．0．1586　D．0．1585

点拨　由正态曲线性质知,其图象关于直线x＝3对称,∴P(X＞4)＝0．5－(2≤X≤4)＝0．5－×0．6826＝0．1587．故选B．

解答　B

反思　注意图象的对称性．

例4　已知随机变量X服从正态分布N(0,σ2),若P(X＞2)＝0．023,则P(－2≤X≤2)等于(　)．

A．0．477　B．0．628　C．0．954　D．0．977

点拨　P(－2≤X≤2)＝1－2P(X＞2)＝0．954．故选C．

解答　C

反思　直接运用公式．

例5　设随机变量X服从正态分布N(2,9),若P(X＞c＋1)＝P(X＜c－1),则c等于(　)．

A．1　B．2　C．3　D．4

点拨　∵μ＝2,由正态分布的定义知其函数图象关于x＝2对称,于是∴c＝2．故选B．

解答　B

反思　注意图象的对称性．

例6　若一个正态分布的概率密度函数是一个偶函数,且该函数的最大值为．

(1)求该正态分布的概率密度函数的解析式;

(2)求正态总体在区间(－4,4]的概率．

点拨　要确定一个正态分布的概率密度函数的解析式,关键是求解析式中的两个参数μ,σ的值,其中μ决定曲线的对称轴的位置,σ则与曲线的形状和最大值有关．

解答　(1)由于该正态分布的概率密度函数是一个偶函数,所以其图象关于y轴对称,即μ＝0．由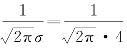,得σ＝4,故该正态分布的概率密度函数的解析式是

(2)P(－4＜X≤4)＝P(0－4＜X≤0＋4)＝P(μ－σ＜X≤μ＋σ)＝0．6826．

反思　解决此类问题的关键是正确理解函数解析式与正态曲线的关系,掌握函数解析式中参数的取值变化对曲线的影响．(www.xing528.com)

例7　设X~N(1,22),求:

(1)P(－1＜X≤3);

(2)P(3＜X≤5);

(3)P(X≥5)．

点拨　将所求概率转化到(μ－σ,μ＋σ],(μ－2σ,μ＋2σ]或[μ－3σ,μ＋3σ]上的概率,并利用正态密度曲线的对称性求解．

解答　∵X~N(1,22),∴μ＝1,σ＝2．

(1)P(－1＜X≤3)＝P(1－2＜X≤1＋2)＝P(μ－σ＜X≤μ＋σ)＝0．6826．

(2)∵P(3＜X≤5)＝P(－3＜X≤－1),

∴P(3＜X≤5)＝[P(－3＜X≤5)－P(－1＜X≤3)]＝[P(1－4＜X≤1＋4)－P(1－2＜X≤1＋2)]＝[P(μ－2σ＜X≤μ＋2σ)－P(μ－σ＜X≤μ＋σ)]＝×(0．9544－0．6826)＝0．1359．

(3)∵P(X≥5)＝P(X≤－3),

∴P(X≥5)＝[1－P(－3＜X＜5)]＝[1－P(1－4＜X＜1＋4)]＝[1－P(μ－2σ＜X＜μ＋2σ)]＝×(1－0．954 4)＝0．0228．

反思　求服从正态分布的随机变量在某个区间取值的概率,只需借助正态曲线的性质,把所求问题转化为已知概率的3个区间上．

易错解读

例8　2011年中国汽车销售量达到1700万辆,汽车耗油量对汽车的销售有着非常重要的影响,各个汽车制造企业积极采用新技术降低耗油量,某汽车制造公司为调查某种型号的汽车的耗油情况,共抽查了1200名车主,据统计该种型号的汽车的平均耗油为百公里8．0升,并且汽车的耗油量X服从正态分布N(8,σ2),已知耗油量X∈[7,9]的概率为0．7,那么耗油量大于9升的汽车大约有________辆．

点拨　由题意可知X~N(8,σ2),故正态分布曲线以μ＝8为对称轴,又因为P(7≤X≤9)＝0．7,故P(7≤X≤9)＝2P(8≤X≤9)＝0．7,所以P(8≤X≤9)＝0．35,而P(X≥8)＝0．5,所以P(X＞9)＝0．15,故耗油量大于9升的汽车大约有1200×0．15＝180(辆)．

解答　180

易错点　服从正态分布的随机变量在一个区间上的概率就是这个区间上,正态密度曲线和x轴之间的曲边梯形的面积,根据正态密度曲线的对称性,当P(X＞x1)＝P(X＜x2)时必然有,这是解决正态分布类试题的一个重要结论．

例9　已知某次数学考试的成绩服从正态分布N(116,64),则成绩在140分以上的考生所占的百分比为(　)．

A．0．3%　B．0．23%　C．1．5%　D．0．15%

点拨　依题意,μ＝116,σ＝8,所以μ－3σ＝92,μ＋3σ＝140,而服从正态分布的随机变量在(μ－3σ,μ＋3σ)内取值的概率约为0．997,所以成绩在区间(92,140)内的考生所占百分比约为99．7%,从而成绩在140分以上的考生所占的百分比为＝0．15%．故选D．

解答　D

易错点　(1)不能正确得出该正态分布的两个参数μ,σ导致计算无从下手;(2)对正态分布中随机变量在3个区间内取值的概率数值记忆不准,导致计算出错．

经典训练

1．在正态分布中,数值落在(－∞,－1)∪(1,＋∞)内的概率为(　)．

A．0．097　B．0．046　C．0．03　D．0．0026

(第2题图)

2．设两个正态分布N(μ1,σ21)(σ1＞0)和N(μ2,)＞0)的密度函数图象如图所示,则有(　)．

A．μ1＜μ2,σ1＜σ2

B．μ1＜μ2,σ1＞σ2

C．μ1＞μ2,σ1＜σ2

D．μ1＞μ2,σ1＞σ2

3．随机变量X服从正态分布N(1,σ2),已知P(X＜0)＝0．3,则P(X＜2)＝_______．

4．工厂制造的某机械零件尺寸X服从正态分布,问在一次正常的试验中,取1000个零件时,不属于区间(3,5]这个尺寸范围的零件大约有多少个?