离散型随机变量及其分布-3.2.1

随机取值的变量就是随机变量,随机变量分为离散型随机变量与连续型随机变量两种,随机变量的函数仍为随机变量．有些随机变量,它全部可能取到的不相同的值是有限个或可列无限多个,也可以说概率“1”以一定的规律分布在各个可能值上．这种随机变量称为离散型随机变量．

方法简述

例1　设离散型随机变量X的分布列为

求2X＋1和|X－1|的分布列．

点拨　设Y＝2X＋1,Y＝|X－1|分别是X的函数,而函数关系可用表格的形式表示出来,然后再写出分布列．

解答　首先列表如下:

从而由上表得两个分布列如下:

2X＋1的分布列为

|X－1|的分布列为

反思　由于X的值不同,Y＝f(X)会取到相同的值,这时要考虑所有使f(X)＝Y成立的X1,X2,…,Xi等值,则P(Y)＝P(f(X))＝P(X1)＋P(X2)＋…＋P(Xi)．

例2　一袋中装有5只球,编号为1,2,3,4,5,在袋中同时取3只,以X表示取出的3只球中的最小号码,写出随机变量X的分布列．

点拨　因为在编号为1,2,3,4,5的球中,同时取3只,所以小号码可能是1或2或3,即X可以取1,2,3．从而可分别求出X所对应的各个值的概率,写出分布列．

解答　随机变量X的可能取值为1,2,3．

当X＝1时,即取出的三只球中最小号码为1,则其他两只球只能在编号为2,3,4,5的四只球中任取两只,故有;

当X＝2时,即取出的3只球中最小号码为2,则其他两只球只能在编号为3,4,5的3只球中任取两只,故有;

当X＝3时,即取出的3只球中最小号码为3,则其他两只球只能是编号为4,5的两只球,故有

因此,X的分布列如下表所示:

反思　求随机变量的分布列,应按以下3个步骤进行:(1)明确随机变量的所有可能取值,以及取每个值所表示的意义;(2)利用概率的有关知识,求出随机变量每个取值的概率;(3)按规范形式写出分布列,并用分布列的性质进行检验．

例3　盒中装有一打(12个)乒乓球,其中9个新的,3个旧的(用过的球即为旧的),从盒中任取3个使用,用完后装回盒中,此时盒中旧球个数X是一个随机变量,求X的分布列．

点拨　从盒中任取3个,这3个可能全是旧的,2个旧的1个新的,1个旧的2个新的或全是新的,所以用完放回盒中,盒中旧球个数可能是3个,4个,5个,6个,即X可以取3,4,5,6．

解答　X的所有可能取值为3,4,5,6．

所以X的分布列为

反思　本题的关键是正确地求出X取某个值时对应的事件个数．

例4　某运动员射击一次所得环数X的分布列如下:

现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为X．

(1)求该运动员两次都命中7环的概率;

(2)求X分布列．

点拨　由于题设条件中所列出的环数最低为6环,且射中6环的概率为0,所以X的最小值取7,当然也可以取8,9,10．从而可得出分布列．

解答　(1)该运动员两次都命中7环的概率为P(7)＝0．2×0．2＝0．04．

(2)X的可能取值为7,8,9,10．

P(X＝7)＝0．04;P(X＝8)＝2×0．2×0．3＋0．32＝0．21;

P(X＝9)＝2×0．2×0．3＋2×0．3×0．3＋0．32＝0．39;

P(X＝10)＝2×0．2×0．2＋2×0．3×0．2＋2×0．3×0．2＋0．22＝0．36．

X分布列为

反思　读懂题意是解决问题的关键,因此在做题时,可不必着急去做,而是要先分析,后做题．例如本题,很多同学误认为X可以取6,7,8,9,10,从而导致错误．

例5　某批产品成箱包装,每箱5件．一用户在购进该批产品前先取出3箱,再从每箱中任意抽取2件产品进行检验．设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品．

(1)用X表示抽检的6件产品中二等品的件数,求X的分布列;

(2)若抽检的6件产品中有2件或2件以上为二等品,用户就拒绝购买这批产品,求这批产品被用户拒绝的概率．

点拨　对于X≥2的情况,由于本题中的X要求取整数,所以X≥2所代表的意义是X＝2与X＝3两种情况．

解答　(1)X可能的取值为0,1,2,3．

X的分布列为

(2)所求的概率为

反思　准确找到随机变量X的取值,明确第一个值所对应的概率,然后代入概率公式进行求解,是解决这类问题的一般步骤．其中,准确找到随机变量的取值是解决本题的关键．

例6　某城市有甲、乙、丙3个旅游景点,一位游客游览这3个景点的概率分别是0．4,0．5,0．6,且游客是否游览哪个景点互不影响,用X表示该游客离开该城市时游览的景点数与没有游览的景点数之差的绝对值．

(1)求X的分布列;

(2)记“f(x)＝2X·x＋4在区间[－3,－1]上存在x0,使f(x0)＝0”为事件A,求事件A的概率;

(3)记“函数f(x)＝x2－3Xx＋1在区间[2,＋∞)上单调递增”为事件B,求事件B的概率．

点拨　游客离开该城市时游览的景点数与没有游览的景点数可以看成是两个取值的问题,因此可以将游客游览的景点数可能取值记为0,1,2,3,相应的游客没有游览的景点数可能取值记为3,2,1,0,则X的可能取值为1,3．从而求出分布列．

解答　(1)设游客游览甲、乙、丙景点分别记为事件A1,A2,A3．

已知A1,A2,A3相互独立,且P(A1)＝0．4,P(A2)＝0．5,P(A3)＝0．6．

游客游览的景点数可能取值为0,1,2,3,相应的游客没有游览的景点数可能取值为3,2,1,0,所以X的可能取值为1,3．

则P(X＝3)＝P(A1·A2·A3)＋＝P(A1)·P(A2)·P(A3)＋＝2×0．4×0．5×0．6＝0．24．

P(X＝1)＝1－0．24＝0．76．

所以分布列为

(2)∵f(x)＝2Xx＋4在区间[－3,－1]上存在x0,使得f(x0)＝0,∴f(－3)·f(－1)≤0,即(－6X＋4)(－2X＋4)≤0,解得≤X≤2．

∴

(2)解法一:因为,所以函数f(x)＝x2－3Xx＋1在区间上单调递增,要使f(x)在区间[2,＋∞)上单调递增,当且仅当,即X≤,从而(www.xing528.com)

解法二:X的可能取值为1,3．

当X＝1时,函数f(x)＝x2－3x＋1在区间[2,＋∞)上单调递增;

当X＝3时,函数f(x)＝x2－9x＋1在区间[2,＋∞)上不是单调函数．

所以P(B)＝P(X＝1)＝0．76．

反思　本题所考查的二点分布的问题,只是进一步地进行了抽象,这里的X的取值并不容易找到,需注意．

例7　以下茎叶图记录了甲、乙两组各4名同学的植树棵数

分别从甲、乙两组中各随机选取一名同学,

(1)求这两名同学的植树总棵数Y的分布列;

(2)每植一棵树可获10元,求这两名同学获得钱数的数学期望．

点拨　本题解题的关键是求出Y的取值及取每一个值的概率,注意用分布列的性质进行检验．

解答　(1)分别从甲、乙两组中随机选取一名同学的方法是4×4＝16(种),这两名同学植树总棵数Y的取值分别为17,18,19,20,21．则

则随机变量Y的分布列为

(2)由(1)知

设这名同学获得钱数为X元,则X＝10Y,

则E(X)＝10E(Y)＝190．

反思　关键是求出Y的取值及取每一个值的概率．

易错解读

例8　已知箱中装有4个白球和5个黑球,且规定:取出一个白球得2分,取出一个黑球得1分．现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出3球所得分数之和．

(1)求X的分布列;

(2)求X的数学期望E(X)．

解答　(1)X的可能取值有:3,4,5,6．

故所求X的分布列为

(2)所求X的数学期望E(X)为:

易错点　求解概率出错导致求解数学期望出错．

例9　某公司有5万元资金用于投资开发项目,如果成功,一年后可获利12%;一旦失败,一年后将丧失全部资金的50%．下表是过去200例类似项目开发的实施结果:

求该公司一年后估计可获收益的期望．

解答　设该公司一年后估计可获得的钱数为X元,则随机变量X的取值分别为50000×12%＝6000(元),－50000×50%＝－25000(元)．由已知条件知随机变量X的概率分布列为

因此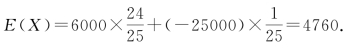

易错点　不理解题意导致出错．

经典训练

1．已知离散型随机变量X的分布列如表所示．若E(X)＝0,D(X)＝1,则a＝_________,b＝________．

2．某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量X表示选出的志愿者中女生的人数,则数学期望E(X)＝________(结果用最简分数表示)．

3．在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次．某同学在A处的命中率q1为0．25,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用X表示该同学投篮训练结束后所得的总分,其分布列为

(1)求q2的值;

(2)求随机变量X的数学期望E(X);

(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小．

4．在10件产品中,有3件一等品,4件二等品,3件三等品．从这10件产品中任取3件,求:

(1)取出的3件产品中一等品件数X的分布列和数学期望;

(2)取出的3件产品中一等品件数多于二等品件数的概率．

5．在1,2,3,…,9这9个自然数中,任取3个数．

(1)求这3个数中恰有1个是偶数的概率;

(2)设X为这3个数中两数相邻的组数(例如:若取出的数为1,2,3,则有两组相邻的数1,2和2,3,此时X的值是2)．求随机变量X的分布列及其数学期望E(X)．

6．某人向一目标射击4次,每次击中目标的概率为．该目标分为3个不同的部分,第一、二、三部分面积之比为1∶3∶6．击中目标时,击中任何一部分的概率与其面积成正比．

(1)设X表示目标被击中的次数,求X的分布列;

(2)若目标被击中2次,A表示事件“第一部分至少被击中1次或第二部分被击中2次”,求P(A)．

7．从集合{1,2,3,4,5}的所有非空子集中,等可能地取出一个．

(1)记性质r:集合中的所有元素之和为10,求所取出的非空子集满足性质r的概率;

(2)记所取出的非空子集的元素个数为X,求X的分布列和数学期望E(X)．

8．某地有A,B,C,D四人先后感染了甲型H1N1流感,其中只有A到过疫区,B肯定是受A感染的．对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是．同样也假定D受A,B和C感染的概率都是．在这种假定之下,B,C,D中直接受A感染的人数X就是一个随机变量．写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)．

9．甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束．假设在一局中,甲获胜的概率为0．6,乙获胜的概率为0．4,各局比赛结果相互独立,已知前2局中,甲、乙各胜1局．

(1)求甲获得这次比赛胜利的概率;

(2)设X表示从第3局开始到比赛结束所进行的局数,求X的分布列及数学期望．

10．某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是,遇到红灯时停留的时间都是2分钟．求:

(1)这名学生在上学路上到第3个路口时首次遇到红灯的概率;

(2)这名学生在上学路上因遇到红灯停留的总时间X的分布列及期望．