回归分析是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛.回归分析按照涉及的变量的多少,分为一元回归分析和多元回归分析;在线性回归中,按照因变量的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析.如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析;如果回归分析中包括两个或两个以上的自变量,且自变量之间存在线性相关,则称为多元线性回归分析.
方法简述
1.基本定义法
例1 19世纪未,德国统计学家恩格尔根据统计资料,对消费结构变化得出一个规律:一个家庭收入越少,家庭收入中(或总支出中)用来购买食物的支出所占的比例就越大,随着家庭收入的增加,家庭收入中(或总支出中)用来购买食物的支出会下降.推而广之,一个国家越穷,每个国民的平均收入中(或平均支出中)用于购买食物的支出所占的比例就越大,随着国家的富裕,这个比例呈下降趋势.恩格尔系数是根据恩格尔定律得出的比例系数,是表示生活水平高低的一个指标,其计算公式为:恩格尔系数=![]() .
.
在我国,判定生活发展阶段的标准是:贫困>60%,温饱50%~60%,小康40%~50%,富裕<40%.根据国家统计局统计显示,随着中国经济的不断增长,城镇居民家庭的恩格尔系数不断下降,居民消费已从温饱型向享受型、发展型转变.如下表所示:
求:(1)根据年份预报恩格尔系数的回归方程;
(2)预报2007年的恩格尔系数;
(3)求相关指数;
(4)作出残差图.
例1答图(a)
点拨 由于问题中要求根据年份预报恩格尔系数,因此选取年份为自变量x,恩格尔系数为因变量y,作出散点图,并根据散点判断x,y是否具有相关关系,从而利用最小二乘法求出回归直线方程.
解答 (1)散点图如图所示:
并由最小二乘法求得线性回归方程为:![]()
(2)由线性回归方程可知,2007年的恩格尔系数为:-0.9018×2007+1845.9=35.9874.
(3)R2=1- =1-
=1-![]() =0.82.
=0.82.
(4)列出编与残差图表如下:
由上表可得残差图如下图所示:
例1图(b)
反思 作残差图是残差分析的一种重要方法,在作图时,横坐标可以选用样本编号,或有关数据,这样作出的图形称为残差图.如果残差点比较均匀地分布在水平带状区域,说明选用的模型比较适合,这样的带状区域越窄,说明所选用的模型的拟合精度越高,回归方程的预报精度也越高.如果残差分布不均匀,应首先确认采集的样本点是否有误,如果有误,就予以纠正,然后再重新利用线性回归模型来拟合数据,如果数据采集没有错误,则需要寻找其他原因.
2.散点图
例2 下表给出了我国从1949年至1999年人口数据资料,试根据表中数据估计我国2004年的人口数.
点拨 作出散点图.
解答 为了简化数据,先将年份减去1949,并将所得值用x表示,对应人口数用y表示,得到下面的数据表:
例2答图
作出11个点(x,y)构成的散点图.
由图可知,这些点在一条直线附近,可以用线性回归模型y=a+bx+ε来表示它们之间的关系.
根据公式可得
这里的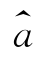 ,
,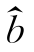 分别为a,b的估计值,因此线性回归方程为
分别为a,b的估计值,因此线性回归方程为![]()
由于2004年对应的x=55,代入线性回归方程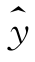 =527.591+14.453x可得
=527.591+14.453x可得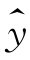 =1322.506(百万),即2004年的人口总数估计为13.23亿.
=1322.506(百万),即2004年的人口总数估计为13.23亿.
反思 通过散点图,准确求出线性回归方程.
3.非线性关系处理
例3 某地区对本地的企业进行了一次抽样调查,下表是这次抽查中所得到的各企业的人均资本x(万元)与人均产出y(万元)的数据:
(1)设y与x之间具有近似关系y≈axb(a,b为常数),试根据表中数据估计a和b的值;
(2)估计企业人均资本为16万元时的人均产出(精确到0.01).
点拨 根据x,y所具有的关系可知,此问题不是线性回归问题,不能直接用线性回归方程处理.但由对数运算的性质可知,只要对y≈axb的两边取对数,就能将其转化为线性关系.
解答 (1)在y≈axb的两边取常用对数,可得lg y≈lg a+b lg x,设lg y=z,lg a=A,lg x=X,则z≈A+b X.相关数据计算如下表所示:
仿照问题情境可得A,b的估计值![]() 分别为
分别为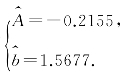 由
由![]() 可得
可得 ≈0.6088,即a,b的估计值分别为0.6088和1.5677.
≈0.6088,即a,b的估计值分别为0.6088和1.5677.
(2)由(1)知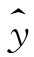 =0.6088x1.5677.
=0.6088x1.5677.
当x=16时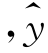 =0.6088×161.5677≈47.01(万元),故当企业人均资本为16万元时,人均产值约为47.01万元.
=0.6088×161.5677≈47.01(万元),故当企业人均资本为16万元时,人均产值约为47.01万元.
反思 非线性关系的处理方法
例4 下表是随机抽取的8对母女的身高数据,试根据这些数据探讨y与x之间的关系.
点拨 所给数据的散点图如图所示,由图可以看出,这些点在一条直线附近.
例4答图
所以![]()
由检验水平0.05及n-2=6,在附录2中查得r0.05=0.707,因为0.963>0.707,所以可以认为x与y之间具有较强的线性相关关系.线性回归模型y=a+bx+ε中a,b的估计值a,b分别为
故y与x的线性回归方程为y=-53.191+1.345x.
反思 结合散点图准确分析.
例5 为了研究某种细菌随时间x变化,繁殖的个数,收集数据如下表所示:
(1)用天数作解释变量,繁殖个数作预报变量,作出这些数据的散点图;
(2)描述解释变量与预报变量之间的关系,计算残差、相关指数R2.
点拨 由题意先作出散点图,判断采用哪种函数模型对样本数据进行拟合,再计算残差与相关指数进行回归分析.
解答 (1)散点图如下图所示:
例5答图
(2)由散点图看出样本点分布在一条指数函数y=C1eC2x的周围,于是令Z=ln y,则
由计算器算得 =0.69x+1.112,则有
=0.69x+1.112,则有 =e0.69x+1.112._________________
=e0.69x+1.112._________________
即解释变量天数对预报变量繁殖细菌的个数解释了99.99%.
反思 从散点图中我们可以看到,样本点分布在某一曲线的附近,而不是在一条直线的附近,所以不能用一次函数来描述它们之间的关系.在回归分析中,通过模型由解释变量计算预报变量时,应注意:(1)回归模型只适用于所研究的总体.(2)回归方程具有时效性.(3)样本的取值范围影响回归方程的适用范围.(4)预报值是预报变量可能取值的平均值.在线性回归模型中,R2表示解释变量对预报变量的贡献率,R2越接近1时,表示线性回归的效果越好;R2越接近0时,线性效果越差.
其中x为高一数学成绩,y为高二数学成绩.
(1)判断y与x是否具有相关关系;
(2)如果y与x是相关关系,求回归直线方程.
点拨 先利用线性相关系数r或散点图判断y与x是否具有相关性,再利用最小二乘法求回归直线方程.
解答 (1)由表格中的数据,利用计算器进行计算得:
由于r≈0.780297>0.75知,有很大的把握认为x与y之间具有线性相关关系.
(2)y与x具有线性相关关系,设回归方程为![]() ,则
,则
∴y关于x的回归方程为![]()
反思 能从散点图直观地判断相关关系,但散点图不明显时,我们就要进行相关性检验,根据相关系数r进行判断.这类问题的解决方法一般分为两步进行.第一步:分析两个变量是否存在线性相关关系(可以利用散点图,也可以利用样本相关系数r);第二步:求出回归直线方程.
例7 假设关于某种设备的使用年限x(年)与所支出的维修费用y(万元)有如下统计资料:
已知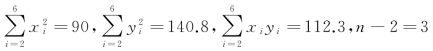 时,r0.05=0.878.
时,r0.05=0.878.
(参考数据:![]() .)
.)
(1)对x,y进行相关性检验,如果x与y具有相关关系,求出回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
点拨 求出回归方程,将使用年限10年代入进行求解维修费用.(https://www.xing528.com)
解答 (1)由题设条件可得![]()
作统计步聚如下:
①作统计假设:x与y不具有相关关系.
②n-2=3时,r0.05=0.878.
③ =112.3-5×4×5=12.3,
=112.3-5×4×5=12.3,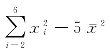 =90-5×42=10,
=90-5×42=10,![]() =140.8-125=15.8,所以
=140.8-125=15.8,所以
④|r|=0.987>0.878,即|r|>r0.05.
所以认为“x与y之间具有线性相关关系”,去求回归直线方程是有意义的.
所以所求的回归直线方程为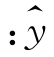 =1.23x+0.08.
=1.23x+0.08.
(2)当x=10时, =1.23×10+0.08=12.38(万元).
=1.23×10+0.08=12.38(万元).
即估计用10年时,维修的费用为12.38万元.
反思 在解决具体问题时,要先进行相关性检验,通过检验确认两个变量之间是否具有相关关系.若它们之间具有线性相关关系,再求出直线方程,否则,即使求出回归方程也是毫无意义的,而且其估计和预测的量也是不可信的.回归直线方程求解需要复杂的运算,随着新课程标准的继续实施和新课程高考改革的不断深入,考查学生数据处理能力,特别是运用计算器等现代技术工具进行数据处理的能力,将是改革的方向之一.对于求回归直线方程时会遇到很复杂的运算,为准确运算,可借助计算器与计算机,先列表求出相关数据,然后求回归系数,从而写出回归直线方程.
易错解读
例8 在彩显影中,由经验可知:形成染料光学密度y与析出银的光学密度x由公式y=![]() 表示.现测得试验数据如下:
表示.现测得试验数据如下:
试求y对x的回归方程.
解答 由题意知,对于给定的公式![]() 两边取自然对数,得
两边取自然对数,得![]()
与线性回归方程相对照可以看出,只要取u=![]() ,v=ln y,a=ln A,就有v=a+bu.这是v关于u的线性回归直线方程,对此我们再套用相关性检验,求出回归系数b和a.题目中所给出的数据由变量置换
,v=ln y,a=ln A,就有v=a+bu.这是v关于u的线性回归直线方程,对此我们再套用相关性检验,求出回归系数b和a.题目中所给出的数据由变量置换![]() ,得到如下数据:
,得到如下数据:
可以求得:r≈0.998.
由于|r|≈0.998>0.75,可知u和v具有很强的线性相关性.再求出b≈-0.146,a≈0.548.所以 =0.548-0.146u.
=0.548-0.146u.
再将u和v置换过来,可得![]()
所以![]()
所以所求的回归方程为![]()
易错点 非线性回归问题有时并不直接给出经验公式,此时我们可以由已知的数据画出散点图,并把散点图与我们已经学习的各种函数,如幂函数、指数函数、对数函数、二次函数等作比较,然后采用变量的置换,把问题转化成线性回归分析问题,使问题得以解决.
例9 关于x与y有以下数据:
有如下两个线性模型:(1) =6.5x+17.5;(2)
=6.5x+17.5;(2) =7x+17,试比较哪一个拟合效果比较好?
=7x+17,试比较哪一个拟合效果比较好?
解答 由(1)得![]() 的关系如下表所示:
的关系如下表所示:
所以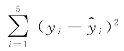 =(-0.5)2+(-3.5)2+102+(-6.5)2+0.52=155.
=(-0.5)2+(-3.5)2+102+(-6.5)2+0.52=155.
所以
由(2)得![]() 的关系如下表所示:
的关系如下表所示:
所以![]() =(-1)2+(-5)2+82+(-9)2+(-3)2=180.
=(-1)2+(-5)2+82+(-9)2+(-3)2=180.
所以
由于![]() ,所以方程(1)的拟合效果比较好.
,所以方程(1)的拟合效果比较好.
易错点 如果对于某组数据采用几种不同的回归方程进行分析,我们可以比较几个R2的值,选择R2大的模型作为这组数据的回归模型.
1.下列关系中,是相关关系的为_________(填序号).
经典训练
①学生的学习态度与学习成绩之间的关系;
②教师的执教水平与学生的学习成绩之间的关系;
③学生的身高与学生的学习成绩之间的关系;
④家庭的经济条件与学生的学习成绩之间的关系.
2.为了考查两个变量x,y之间的线性相关关系,甲、乙两同学各自独立地做10次和15次试验,并利用最小二乘法求得回归直线分别为l1和l2.已知在两人的试验中发现变量x的观测数据的平均值恰好相等,都为s,变量y的观测数据的平均值也恰好相等,都为t,那么下列说法中正确的是_________(填序号).
①直线l1,l2有交点(s,t);
②直线l1,l2相交,但是交点未必是(s,t);
③由于斜率相等,所以直线l1,l2必定平行;
④直线l1,l2必定重合.
3.下列有关线性回归的说法中,正确的是________(填序号).
①相关关系的两个变量不一定是因果关系;
②散点图能直观地反映数据的相关程度;
③回归直线最能代表线性相关的两个变量之间的关系;
④任一组数据都有回归直线方程.
4.下列命题中:
①线性回归方法就是由样本点去寻找一条贴近这些样本点的直线的数学方法;
②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示;
③通过回归直线![]() 及回归系数
及回归系数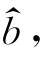 可以估计和预测变量的取值和变化趋势.
可以估计和预测变量的取值和变化趋势.
其中正确命题的序号是_________.
5.已知回归方程为![]() ,则x=25时
,则x=25时 的估计值为_________.
的估计值为_________.
6.下面是水稻产量与施化肥量的一组观测数据(单位:千克/亩):____________
(1)将上述数据制成散点图;
(2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?水稻产量会一直随施化肥量的增加而增长吗?
7.随着我国经济的快速发展,城乡居民的生活水平不断提高,为研究某市家庭月平均收入与月平均生活支出的关系,该市统计部门随机调查了10个家庭,得数据如下表所示:
(1)判断家庭平均收入与月平均生活支出是否相关?
(2)若二者线性相关,求回归直线的回归方程.
8.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]()
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
9.在研究硝酸钠的可溶性程度时,对于不同的温度观测它在水中的溶解度,得观测结果如下表所示:
由资料看y与x呈线性相关,试求回归方程.
10.某企业上半年产品产量与单位成本资料如下表所示:
(1)求出线性回归方程;
(2)指出产量每增加1000件时,单位成本平均变动多少?
(3)假定产量为6000件时,单位成本为多少元?
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




