主要随机波动率模型介绍

传统的BSM模型取得了巨大的成功，然而我们在之前多章内也提到了其常数波动率假设产生的模型风险。从原理上来说，本章第二节和第三节，都是为了说明这样一个问题：在市场上观测到的隐含波动率曲线所呈现的微笑或倾斜结构，与常数波动率假设所必然导致的水平波动率差别过大。显然，BSM的模型假设在真实世界中是不成立的。

处于更准确地为期权定价的目的，在实操中，对于复杂结构的衍生品结构，我们往往需要使用随机波动率模型来优化期权价格的计算。随机波动率模型认为波动率本身是随着价格的变化而变化的，并且这个变化过程是一个随机过程，在数学上而言，随机波动率模型的思路是将标的资产价格过程中的波动率描述为一个由均值回归和方差加以控制的随机过程，并以此对波动率随着时间的增量进行动态刻画，进而提供对期权进行更高精度的定价的可能性。

随机波动率模型的校准往往非常复杂，大部分情况下都是通过对于期权的市场价格或隐含波动率的拟合而进行的。换言之，对于每一个随机波动率模型，在参数已经确定的情况下，其能够确定一个唯一的资产价格随机过程，并且根据这个价格的随机过程，可以得到一个唯一的、确定性的隐含波动率曲面（尽管曲面函数可能很复杂，甚至不存在解析公式，需要用数值方法计算）。反之亦然，对于任何一个满足Dupire公式的隐含波动率曲面，在确定所使用的随机波动率模型以后，均可以逆向校准出一个随机波动率模型及其全部参数。

在本节中，我们会粗略地介绍几种可能常用的随机波动率模型的函数形式和模型特性，包括CEV、Heston、SVI和SABR。对于大部分的模型，我们不会深入到具体的模型推导和技术细节中去，由于相应的方法论是明确的，有兴趣的读者亦可以参考Cox＆Ross、Heston、Gatheral等人的原始文献，他们的工作包括了对拟合算法非常详尽的说明和推导。

首先，我们从常数波动率模型开始（如果一个常数也能称之为模型的话），一个常数波动率模型所隐含的标的资产价格的随机过程，正如我们一再提及的，如下：

特别地，在风险中性测度之下，其将会变为：

然而，常数波动率首先要面对的问题，就是在股票市场中呈现的隐含波动率倾斜的问题，即当股票资产价格下跌时，其波动率将会上升，这非常直观的与常数波动率模型不符。

Cox和Ross（1975）提出了CEV模型，即常弹性方差模型。在该模型中，标的资产的价格过程为：

其中，弹性系数β∈（0,2]，可以看到，当β=2时，CEV所假设的资产价格过程与BSM模型完全相同。而当2β＜时，波动率将会随着股价的下降而上升。此时的资产价格分布能够较好地解释实际中观测到的资产价格和波动率的负相关，进而更好的解释波动率微笑。特别的，狭义概念上的CEV模型，特指1β=的情况。而在本章节的介绍中，我们也以此作为例进行阐述。

为什么称其为常弹性方差模型，可以看到：

因此，从经济学中的弹性定义可知，下式成立：

即，股票价格的瞬时方差对于股票价格的弹性为常数β。

我们略过复杂的模型推导，仅介绍大致逻辑和结论，CEV模型下的期权定价逻辑和BSM的推导过程高度一致，利用动态对冲思想构建一个股票债券组合，并利用几乎相同的方法可以得到CEV模型下，期权定价所应当满足的偏微分方程：

可以看到，这与BSM PDE非常接近，确切的来说，在2β=时，这就是BSM PDE，与之前介绍的CEV特征相同。

Heston于1993年在CIR模型的基础之上得到了如下的偏微分方程：

其中，St、Vt分别是标的资产的价格和价格的方差，Ws和Wv为两个维纳过程，且二者相关系数为ρ，可以看到，标的资产的价格过程是一个参数为非常数的扩散过程，但是波动率是一个均值回归过程，其中k为回归速率，θ为方差的长期均值，而η则为波动率的方差。

为什么说波动率是一个均值回归过程，可以看到，在这个模型形式中，价格的方差将会收敛于长期均值θ，当短期的方差大于均值时，会产生一个负向的dt项，而当短期的方差大于均值时，则会产生一个正向的dt项，且将会以k作为乘数随时间影响dVt。因此，这种长期会收敛于固定值的过程，被称为均值回归过程。

那么为什么波动率需要是一个均值回归过程呢？简单来说，波动率从直觉上来说是有界的，即任何资产的波动率都不会变得非常大，也难以长期维持得非常小，即使给定无限的时间也是如此。这一点和资产价格是有显著不同的，在无限的时间假设下，由于通货膨胀率是正的，资产价格理论上而言，最终是会变得无穷大的，因为这个时候货币的购买力已经变得非常低。因此波动率需要是一个均值回归过程，而从长期来看，股票价格往往不能被假设为一个均值回归过程。

Heston模型使用了随机波动率来替代BSM模型的常波动率假设，这使其能够在不丧失模型严谨性的前提下，更好地贴近实际情况。并且，Heston模型对于欧式期权的定价存在解析解，因此当Heston模型的参数给定以后，计算Heston模型下的隐含波动率可以使用我们在本章第一节中介绍的二分法来解决。当然，给定市场期权价格，拟合Heston模型参数就没有这么简单了。

在隐含波动率曲线的描述上，有充分的实证研究表明，Heston模型对于隐含波动率的曲线描述效果较好，进而对欧式期权的定价有显著的指导意义。(www.xing528.com)

然而，在没有其他模型补充的情况下，Heston模型也至少有两个主要问题需要解决：

1.Heston模型的参数拟合需要使用完整的期权横截面数据，良好的拟合效果的代价是非常慢，尽管可以使用快速傅里叶变换（Fast Fourier Transform，FFT）等技术加速这个过程，但是相比于其他模型的拟合而言，即使使用这些相对复杂且难以实现的技术，Heston的拟合依然非常慢；

2.实证结果显示，Heston模型仅对有良好流动性的欧式期权的定价效果较好，在涉及奇异结构的情况下，直接使用Heston模型的效果不佳。

问题2是有解决方案的，Derman提出的局部波动率模型（Local Volatility）可以解决对于场外奇异结构的定价问题，只要存在连续的隐含波动率曲面，我们会在本节第七部分详细地讨论这个问题。而问题1，目前看来没有特别好的解决方案，仅能够通过上硬件，即配置更多的算力来解决。这使得在实务中，大部分情况下，即使对于模型要求较高的场外结构而言，使用Heston模型也经常显得过于奢侈，有多种其他拟合较快，同时模型假设也较为严谨的模型可以达到相同的效果，比如说SABR或者SVI模型。

SABR是由Hagan等人于2002年提出的，对资产的远期价格进行描述的随机波动率模型。SABR为Stochastic Alpha Beta Rho的缩写。其函数形式为：

可以看到在SABR中存在4个常数参数，α、β、ρ、ν。在上述公式中，Ft为资产远期价格的过程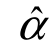，为资产远期价格过程的波动率的随机过程；常数ν＞0被定义为波动率的波动性，当ν=0时，可以看到，SABR模型将会坍缩为一个CEV模型；偏移系数β为常数，且β∈[0,1]，主要用来描述资产远期价格与平值期权波动率之间的关系，当β=1时，SABR模型所假设的资产价格分布将会是一个对数正态分布，正如我们在对股票价格进行BSM模型推导时所假设的，当β=0.5时，SABR模型将会坍缩为CIR模型，而当β=0时，SABR假设的资产价格分布就会变成一个正态分布。

由于函数形式较为简单，我们在此给出SABR模型所对应的隐含波动率曲面函数：

在平值处的波动率计算：

在非平值的波动率计算：

SABR模型的拟合方法较为简单，甚至可以直接通过极大似然估计（Maximum Likelihood Estimate，MLE）进行拟合，速度较快。同时其模型形式可以近似的求得一个隐含波动率的曲线函数，因此直接从隐含波动率曲面即可完成拟合，进而对于所有没有实际报价的行权价格的期权也可以完成定价。更好的是，SABR可以赋予模型参数直观的图像意义，且这个图像意义是单调的，因此在实操中，SABR被广泛地使用在利率等主要资产类别的衍生品建模上。

SVI是由Gatheral在2004年提出的一个很流行的波动率曲线拟合模型。对于某一个特定期限的期权合约而言，其隐含波动率曲线可以用下式拟合：

与SABR相似的，SVI模型的5个参数具有直观且单调的图像意义。由于其自由度更高，在某种意义上而言，其图像调整的灵活性是高于SABR的。同时，有文献证明SVI模型在极端实值或虚值部分是近似线性，即满足Roger Lee的动量方程的，且在T趋于无穷大时，SVI亦展示了对于Heston模型的收敛（事实上，我个人的实证研究发现在1个月左右的时间处，误差即小到满足大部分场外衍生品的定价和风控要求，在3个月左右，几近于没有区别）。因此，尽管SVI是一个实际意义上的参数模型，其对于随机波动率模型良好的收敛性依然使得我们不得不在介绍随机波动率模型时进行阐述和介绍，而非简单的将其看作是一个参数模型。

值得强调的一点是，SVI的拟合是基于某一条特定到期期限的隐含波动率曲线而非曲面的，如果要形成曲面的话，可以使用本节第二部分中介绍的方差线性插值的做法进行处理。

SVI模型提供了一个非常接近于随机波动率模型，然而在拟合和运算上迅速且高效的参数模型。我们在此介绍Zeliade Systems在2009年提出的SVI模型的Quasi-Explicit优化法逻辑，对具体算法感兴趣的读者可以查阅原始文献“Quasi-Explicit Calibration of Gatheral’s SVI model”。该算法优化效率高，且对于参数拟合的稳定性强。

Quasi-Explicit算法的主要逻辑是将原始对于五个参数的优化问题进行拆分和降维，并将其转化为内外层两个优化问题，以提升运算效率：

内层的优化问题中函数平滑且严格凸，因此极值唯一。

外层优化中的函数存在多个极值。因此使用成熟的Nelder-Mead Simplex优化算法，通过引入模式搜索，对初始点的选择包含了对于过去的记忆。因而优化过程中反复得到相同的局部最优解的概率较低，其优化结果将会显著好于随机初始点的选择方法。

Quasi-Explicit算法无法保证一定能找到全局最优，但是对于业务开展而言，全局最优不是必需的。如果可以接受为了提升速度而选择相对不那么严谨的近似模型，在同一个较为严谨的模型中选择无法保证全局最优的优化方法，亦是高度可接受的。

因此在主流的厂商定价系统中，Quasi-Explicit算法都是最主要的解决方案。