交易策略：Delta策略、跨式策略-金融工程原理

1.Delta策略

这类策略，主要通过持有期权、期货、标的资产以获取Delta或者说方向性敞口获利。

一个简单的例子是持有一个欧式看涨期权，当标的资产价格上涨时，欧式看涨期权的价格将会上涨，而标的资产价格下跌时，欧式看涨期权的价格就会下跌。在Delta面前，其余所有的Greeks对于损益的影响均远小于Delta。

当然，欧式看涨期权价格比较高，尤其是平值和实值期权，那么通过卖出一个虚值期权构建一个价差组合，可以通过放弃上行收益获得一个更加廉价的成本。同时也可以降低Gamma，Theta和Vega敞口。

与此同理，任何涉及对标的资产的方向性敞口的策略，往往被看成是一个Delta策略。比方说Covered Call（买入标的资产，同时卖出看涨期权），Protective Put（买入标的资产，买入看跌期权），Zero Cost Collar（买入看涨期权同时卖出看跌期权使两个合约的权利金相等以达到零成本）等等。这些策略都带有一定的对于标的资产未来走势的看法，不同之处在于最终损益由于行权价格，到期时间的不同，可能会呈现不同的结构，但是本质是完全一样的。

2.Gamma/Theta策略

这类策略，主要是通过持有期权头寸，来赚取时间价值或者赚取Gamma。典型策略包括跨式策略（同时买入或者卖出相同行权价格和到期日的看涨看跌，往往是Gamma最大的平值附近），宽跨式策略（和跨式类似，只是看涨的行权价格高于看跌的行权价格），以及其他Delta中性，同时主要交易近月合约的策略。这种通过交易Gamma，对冲Delta以维持中性以赚取标的市场波动产生的Gamma利润的策略，叫作Gamma Scalping。

赚取时间价值听起来非常好理解，卖出一堆期权，然后期望资产价格尽可能不要变动，理想情况下标的资产价格完全没有变动，期权时间价值坍缩到0，我直接能够赚取这些期权的时间价值。然而事情真的这么简单吗？

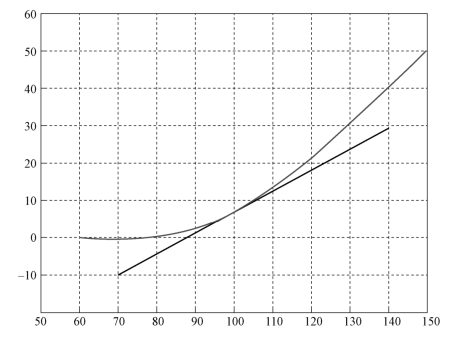
图10-5　Gamma-Theta交换策略

回想我们之前在推导BSM公式中得到的结论，如果我们不通过不断调整头寸，使得股票-债券组合始终和期权价值一致的话，我们无法完整复制，也就是说，无论我们把期权卖了多高的价格，只要我们不这样不断地调整头寸，我们都有大于0的概率亏损。

那么我们怎么进行头寸调整呢？

那个股票-债券组合里面的股票仓位at，不就是Delta吗，我们可以时时刻刻通过买卖标的资产或者期权来保持整个组合的Delta为0。那我们的组合，根据第一节中的解释，就完全变成了一个Gamma-Theta之间的博弈交换。

这个交换是如何完成的？

我们重新回到期权价格随着标的资产价格波动的图中。在该张图中，假设标的资产价格为100，与行权价格相符，那么我们需要多少单位标的资产复制这个期权？Delta单位。在图形上，体现为蓝线，即期权价格曲线在标的资产价格为100处的切线。

但是持有期权比持有Delta单位的标的资产更加有利。我们可以看到，当标的资产价格上涨高于100时，很明显，由于正Gamma的存在，我们会有一个正向的Delta，上涨幅度越大，我们的Delta就越大，这很明显是对权利方有利的，因此也可以看到，期权价格会高于蓝线。

那么下跌的时候呢？正Gamma会导致一个负向的Delta，下跌幅度越大，Delta负值程度也越大，这依然对权利方有利，期权价格依然高于蓝线。

可是这是这个瞬间期权价格的损益，一旦市场重新回到100，这个损益岂不是没了？权利方还要损失时间价值，这听起来似乎是纸上富贵，不是吗？

当然不是。考虑我们在BSM里面做的调仓。当市场上涨，由于正Gamma的存在，我们原本Delta中性的组合会获得一个正向的Delta，为了保持Delta中性，我们应当进行什么操作？做空Delta，无论是卖出标的资产（此时处于高位），卖出期货（同样处于高位），卖出看涨期权（依然处于高位）或者是买入看跌期权（处于低位），我们都在以一个比原本Delta中性时更好的价格进行交易。同理，在市场下跌时，我们也同样可以以更好的价格交易相关资产。正向的Gamma在不断地调整头寸，使得我们Delta中性的过程中，不断地在让我们执行买低卖高的操作，而这一切，完全不需要我们对市场有任何的预测。

那么同理，当我们做多Theta，卖出Gamma的时候，我们就面临自动的买高卖低操作。但是同时，正向的Theta可以让我们赚取时间价值，以弥补我们买高卖低的亏损，在本章第一节中我们已经对此进行了介绍。

那么，既然卖出Theta会导致我们调仓的时候买高卖低，那么不调仓不就好了吗？为什么我们还要做这种一定导致亏损的事情？

答案是，如果不调仓，会导致更大的亏损。对此，我们回到期权损益的计算公式：

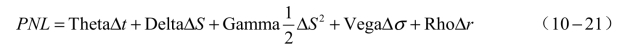
当我们持有负向Gamma的时候，为简便起见，我们假设这个Gamma恒定。当标的资产变动一单位时，我们Gamma损益为：

而当标的资产变动两个单位的时候呢？如果我们在资产变动一个单位的时候就把Delta重新平衡到0，我们的损益将会是：

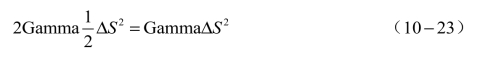(www.xing528.com)

如果我们不平衡呢？我们的Gamma损益会是：

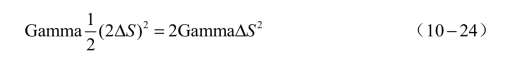
可见，鸵鸟战术会使得我们的亏损变成积极保持我们Delta中性的两倍。除非标的资产有超过2/3的概率回到原点，否则我们的期望收益都是负的。谁给我们的勇气去假设标的资产会回到原点呢？要知道，我们之前对于标的资产的假设是一个布朗运动，标的资产贴现后的现值的上涨下跌期望完全一致，这并不是一个均值回归的过程。很明显，在做空Gamma做多Theta时不平衡组合大概率会导致更大的亏损。

一个惨痛的教训来自股灾后的50ETF期权市场。在几个月内，50ETF被作为指数的稳定器，呈现窄幅波动。在这个时间段内，做多Theta，完全是稳赚不赔，甚至不需要调仓，因为50ETF无论上涨还是下跌，都会回到起始点附近。在那几个月，50ETF的波动一度低至年化8％，这是一个难以想象的低波动（要知道，外汇市场的波动可能都高于8％）。很多基金经理在那半年通过做空Gamma做多Theta（简而言之，卖期权）赚到了非常稳定的收益。然而随后50ETF的逻辑变成了拉指数，构建白马龙头的大牛市的工具。50ETF的迅速上涨，导致做空Theta很快产生大量亏损。在短短几天之内，不对冲Gamma导致的亏损就超过了之前几个月赚取的Theta总和。这直接导致了一些基金经理在大牛市中爆仓。

那么相反的，当做多Gamma而做空Theta的时候，不平衡组合就变得有利可图。道理是一样的，平衡会导致期望收益降低。

但是不管如何，根据Feynman Kac，理论上来说，如果我们不断地把Delta敞口调整到0的话，当一开始的波动率是完全准确的时候，Gamma和Theta双方损益都为0。然而，实际中真的这么操作，一定会导致损益是0吗？

答案是否定的，因为波动率预期可能会变，这会导致路径依赖的Gamma，如果在急需对冲的时点Gamma非常大的话，会导致Gamma的多头出现额外的利润。同时，理论假设往往不考虑交易成本，而实际上，很大的Gamma会导致频繁调仓，交易成本和买卖价差会吃掉一部分利润。

这是这个问题的一种标准答案，然而从交易的角度来说的话，这两点加在一起也没多少。如果一个市场如此疯狂，或者交易成本如此之高的话，参与这个市场又有多少实际意义呢？

3.套利策略

什么是套利？一价定律告诉我们，如果有两个自筹资金（即可以不依靠外部现金流注入而维持）的组合，如果在某一刻这两个组合的价值相等，那么在每时每刻这两个组合的价值都应当相等。

那么如果不相等怎么办？很简单，通过买低卖高，然后等待二者价格收敛平仓赚取差价，就是我们所说的套利。

在期权上有什么套利策略吗？我们在此介绍一个最简单的套利策略：看涨看跌平价（Put-Call Parity）。

我们考虑一个欧式看涨期权和一个欧式看跌期权。欧式看涨期权的Delta是N（d1），欧式看跌期权的Delta是−N（−d1）=N（d1）−1。

所以我们可以得到两个特性：

（1）买入一个欧式看涨期权，卖出一个欧式看跌期权，如果二者行权价格相同的话，这个组合的Delta将会是N（d1）−N（d1）+1 =1，这个Delta会等价于一个期货多头或者一个标的资产，同时，行权价格相同的看涨看跌的Gamma，Vega大小方向均相同，一买一卖我们完全对冲掉了这些敞口。

（2）考虑两个组合，一个是一个看跌期权多头和一单位满足这个看跌期权义务的标的资产，另一个是一个看涨期权多头和按照无风险利率到期将会满足这个看涨期权义务的无风险收益资金。并且看涨期权和看跌期权的行权价格，到期时间和标的资产完全相同。

我们分析到期标的资产价格不同的可能性，当标的资产价格高于行权价格时，看涨期权行权，看跌期权不行权，两个组合的价值均为标的资产价值。当标的资产价格低于行权价格时，看涨期权不行权，看跌期权行权，两个组合的价值均为与行权价格相等的现金。无论如何这两个组合到期价值均相等。

根据一价定律，这两个组合到期价值相等，则在之前的每一个时点，这两个组合的价值均相等，这意味着：

也就是说，如果在市场上发现的行权价格相同，到期时间相同，标的资产相同的看涨和看跌期权，如果上述等式不成立，并且利润空间大于买卖价差和手续费的话，套利策略即成立。这就是看涨看跌平价套利策略（Put-Call Parity）。

听起来很厉害。抱歉，市场上还有一万八千个交易员也都在盯着，还有另外三千个程序在自动搜索这个套利机会。这么简单的所有人都知道的策略，怎么可能如此轻易出现。即使偶尔出现一次，也是先到先得，谁家电脑、网络、程序快，谁就能够捡到这个硬币，最后这个策略就变成了军备竞赛，门槛如此之低，最后大家都挣不到钱。

有一个面试题是这么问的，如果一个资产现在价格是100，并且没有任何下跌的风险，那么平值欧式看跌的价值是0，对不对？这很好理解，不存在下跌的可能性，那看跌期权就不会行权，价值当然是0。那么假设无风险收益率为0的话，这项资产现在平值的欧式看涨期权的价值是多少？

答案是0，根据看涨看跌平价即可得到。

听起来非常违反常识，如果不存在下跌的风险的话，看涨期权怎么看都是稳赚不赔，怎么可能是0呢？这毫无疑问是一个好问题，当然一个更好的问题可能是：如果一个价格100的资产，没有任何下跌风险，即资产价格不会低于100的话，那有什么理由这个资产的价格还是100？只有一种可能性，这个资产的价格也不存在高于100的可能性，它的价格被冻结在100。那么看涨期权的价格当然也只能是0。

这两个案例告诉我们什么？

世上没有白吃的午餐。谁也不是世界上最聪明的人，如果一个机会看起来好到不像是真的，那么，大概率它就不是真的。

培养正确的收益-风险意识，其重要性远远大于知识本身。