伊藤积分与几何布朗运动

在实际的金融环境中，我们会构建一个数学模型来描述资产的价格或者收益率的变化过程，并在此基础上对衍生品进行定价。一个主流的用来描述资产价格和收益率的模型如式（9-11）。

在上面的公式中，St是标的资产在t时刻的价格，μ（St,t）是标的资产在t时刻，在股价为St时的收益率，或者叫漂移率（Drift），σ（St,t）是标的资产在t时刻，在股价为St时收益率的波动率，而dWt是一个概率分布，其服从均值为0，方差为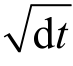的正态分布。

这个公式很好理解，在任何一个瞬间，资产价格的收益率都服从于一个正态分布，其均值为这段时间的短期趋势μ（St,t）dt，同时还有一个市场交易导致的随机扰动σ（St,t）dWt。

为什么dWt服从均值为0，标准差为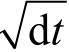的正态分布？

根据定理9.1中心极限定理的结论，我们定义随机扰动项服从一个正态分布，其扰动幅度（标准差）已经由σ（St,t）规定，则我们将随机扰动项标准化为一个标准正态分布。根据中心极限定律，在单位为1的时间内，其标准差为1，那么在dt的时长内，这个扰动项的概率分布的方差即为dt，其标准差为。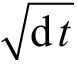

把式（9-11）两边同乘以St，我们得到式（9-12）

接下来，为了简化起见，我们再假设μ（St,t）=μ,σ（St,t）=σ均为常数。式（9-12）就缩为式（9-13）

我们现在计划要得到St的概率分布。在微积分上，只需要对微分方程的两边同时积分即可。如果我们够幸运的话，我们可以找到这个积分的解析解，然后解决这个问题。如果我们实在找不到的话，我们也可以通过计算机的数值方法来解决这个问题。最简单直接然而有效的方式是欧拉方法，直觉上来说就是求阴影部分面积，在此我们不过多阐述。

然而在式（9-13）中却没有这些操作。因为dSt是一个随机过程，dWt是一个服从正态分布的随机变量，这使得dSt在传统的微积分观点中处处不可积。那么是否有什么方法可以让我们用和微积分比较相似的方法对dSt或者df（St）进行积分呢？答案是肯定的，这个方法叫作伊藤引理（Ito’s Lemma）。(www.xing528.com)

为了简便起见，我们只介绍一个简单版本。

定理9.3（伊藤引理）假设存在一个布朗运动tW和一个二次可导函数，资产价格服从

dSt=μStdt+σStdWt

则有以下等式成立：

对式（9-13）使用伊藤引理，我们可以做出计算如式（9-14）：

对两端积分，我们可以得到式（9-15）和式（9-16）：

其中Wt为一个均值为0，标准差为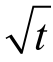的正态分布。

因此我们可以看到，在我们刚才假设的过程下，St服从一个对数正态分布，所谓对数正态分布是指一个随机变量的对数服从正态分布，因此这个随机变量本身是恒正的，也和资产一定具有价值的现实情况相符。