内在价值与时间价值-金融工程原理

内在价值（Intrinsic Value）是多方行使期权时所具有的价值和0之间的最大值。它反映了期权持有者马上执行期权可获得的收益。期权的“内在价值”可有可无，如平价或溢价的期权合约便没有“内在价值”。

时间价值（Times Value），也称投机价值，即期权费减去“内在价值”后剩余的部分。时间价值是指在期权有效期内标的资产价格波动为期权持有者带来收益的可能性所隐含的价值，反映了交易商愿意为标的资产价格波动的不确定性所支付的代价。显然，标的资产价格的波动率越高，期权距离到期期限的时间越长，期权的时间价值就越大。当内在价值接近0时，不确定性是最大的，时间价值最高。对于深度实值看涨期权与深度虚值看涨期权来说，其时间价值极低。

期权的价格应该等于内在价值和时间价值之和。内在价值原理是指期权的价格决不会低于其内在价值。如果市场中给出期权价格低于内在价值，则有套利。我们看一个例子。

例8.4　美式看涨期权S=83，X=80，如果C=2，期权交易商将进行怎样的套利交易行为？

解：在这个例子中，期权价格小于内在价值，因此有套利机会。投资者借入2元，买入看涨期权，立刻执行，获得3元，除去2元，套利收益1元。

1.欧式看涨期权的内在价值与时间价值

无收益的欧式看涨期权在到期日的内在价值为max（ST−X,0），在t时刻的内在价值等于max（St−Xe−r（T−t）,0）。

图8-1给出了欧式看涨期权的价格曲线。从中可以看出，对无收益资产的情况。看涨期权价格的上限为S，下限为max[S−Xe−r（T−t）,0]。期权价格下限就是期权的内在价值。当内在价值等于零时，期权价格就等于时间价值。时间价值在S=Xe−r（T−t）时最大；当S趋于0和∞时，时间价值也趋于0，此时看涨期权价值分别趋于0和S-Xe−r（T−t）。特别地，当S=0时，C=c=0。

图8-1　欧式看涨期权的价格曲线(www.xing528.com)

2.欧式看跌期权的内在价值与时间价值

下面我们讨论无收益资产看跌期权的情形。无收益资产欧式看跌期权在T时刻的内在价值为max（X−ST,0），在t时刻的内在价值为　max（Xe−r（T−t）−St,0）。

图8-2给出了欧式看跌期权的价格曲线。欧式看跌期权的上限为　Xe−r（T−t），下限为max[Xe−r（T−t）−　S,0]。当　Xe−r（T−t）−S＞0时，它就是欧式看跌期权的内在价值，也是其价格下限，当　Xe−r（T−t）−S＜0时，欧式看跌期权内在价值为0，其期权价格等于时间价值。当S=Xe−r（T−t）时，时间价值最大。当S趋于0和∞时，期权价格分别趋于Xe−r（T−t）和0。特别地，当S=0时，p=Xe−r（T−t）时间价值为0。当S趋于∞时，p=0。对于无收益资产欧式期权，时间价值最大点：St=Xe−r（T−t）。

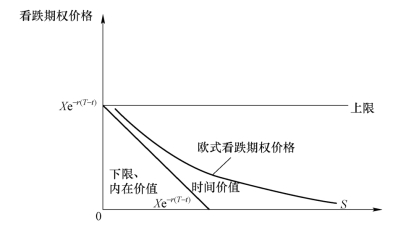
图8-2　欧式看跌期权价格特性

r越低，期权期限越长，标的资产价格波动率越高，看跌期权价值以0为中心越往右上方旋转，但不能超过上限。

3.美式看涨看跌期权的内在价值与时间价值

美式看涨期权的内在价值为max（S-X，0），美式看跌期权的内在价值为max（X-S，0）。对于美式看涨期权多头，内在价值=max（S-X，0），时间价值=C-max（S-X，0）。对于美式期权，时间价值最大点为S=X。图8-3给出了美式看跌期权的价格曲线。

图8-3　美式看跌期权的价格曲线