之前我们讨论了利用衍生品与股票复制无风险资产。如果引入无风险债券,与股票适当搭配头寸形成资产组合,能否复制出与衍生产品相同的现金流?
1.无风险资产与股票复制期权
假设一只无红利支付的股票,当前时刻t价值是S,期末T时刻价值是S1,有两种市场状态,即S1只可能取两个值:一是uS,u>1;二是dS,d<1。我们现在想要确定的是依附于该股票的看涨期权的价值。假设无风险利率为r(d<er(T−t)<u)。
我们构造这样一个投资组合,使它与看涨期权的价值特征完全相同。以无风险利率r借入一部分资金B(相当于卖空无风险债券),同时在股票市场上购入N股标的股票。由于这一组合完全复制期权的价格变动,那么在期初,组合的价值应该与看涨期权的价值相同,即有NS–B=f。
股票和期权的二叉树模型分别如下:
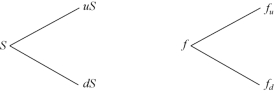
图3-7 股票和期权的二叉树图
则期末时我们有:

解得:
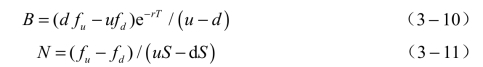
我们的目的是求得f,则有:
![]()
其中:
p=(erT−d)/(u−d)
显然,这里得到的期权价格f与我们之前利用风险中性定价法得到的结论是一样的。下面我们来看一个例子。
例3.9 一份看涨期权,到期时间为1年,执行价格112元;标的股票当前的价格为100元,无风险利率为8%。一年后,股票的价格或是上升到180,或是下降到60元,则期权的价格为多少?(用复制、Delta对冲以及风险中性法分别验证)需要借入多少资金来购买多少股票可以复制该期权?(https://www.xing528.com)
解:根据已知条件,可以得到股票和期权的二叉树模型分别为:
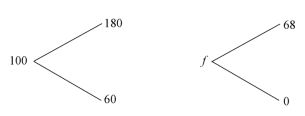
图3-8 股票和期权的二叉树图
方法1,delta对冲法。
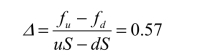
60×0.57e−0.08=100Δ−f
f=25.43元
方法2,无风险定价法。先求出风险中性概率:
180p+60×(1−p)=100erT
求出风险中性概率p=0.4。进一步求得期权价格为:
f=68×0.4e−rT=25.43元
方法3,复制方法:借入L份无风险资产,买入Δ份股票:
180Δ−LerT=68
60Δ−LerT=0
求出Δ=0.57,L=31.57。因此:
f=25.43元
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




