二叉树模型下的欧式期权平价关系依旧成立

假设一只无红利支付的股票，当前时刻t价值是S，期末T时刻价值是S1，假定有两种市场状态，即S1只可能取两个值：一是S1=u×S，u＞1；二是S1=d×S，d＜1，即如下的二叉树模型：

图3-6　股价变化与期权的二叉树图

首先无套利市场中，必须满足：

d＜erT＜u

其中，d为股票下跌的幅度，u为股票上涨的幅度。

运用反证法：当　d≥erT时，我们可以借入S，买入股票获得套利收益。而当erT≥u时，可通过卖空股票，贷出资金获得套利收益。

我们现在想要确定的是当无风险利率为r时依附于该股票的看涨期权的价值f是多少？

和例3.6类似，我们可以建立一个包含衍生品头寸和基础资产头寸的无风险的资产组合。若数量适当，基础资产多头的赢利就会与衍生品的空头亏损相抵，实现瞬间无风险。无风险组合的收益率必须等于无风险利率，由此推出期权的价格。

假定Δ份股票多头+1份看涨期权空头可以组成一个无风险资产，其未来价值为：

uSΔ−fu=dSΔ−fd

可得：

当前时刻，组合的价值为：

（uSΔ−fu）e−rT=ΔS−f

代入Δ可得：(www.xing528.com)

我们将p称为风险中性概率。

因此，当我们面对一个一般二叉树模型时，可以得到期权的价格为：

f=e−rT[pfu+（1−p）fd]

其中：

例3.7　假设一只不支付红利的股票目前的市价为10元，我们知道在3个月后，该股票价格要么是11元，要么是9元。假设现在的无风险年利率等于10％，求一份3个月期协议价格为10元的股票欧式看涨期权的价值，并求出相应Delta值。

解：根据已知条件，可算出：

u=1.1　d=0.9　Δ=0.5　p=0.63

看涨期权价值为：

f=e−rT［pfu+（1−p）fd］=0.61元

若为看跌期权：

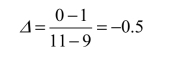
（注意：针对看跌期权，其Δ值总为负）

进一步求出看跌期权的价格　0.36f′=　元。

在例3.7中，二叉树模型下的欧式期权平价关系依旧成立。请读者自行验证。