年金 - 了解七种金融关键信息与财务收益

年金是现金流计算的一种最为简单的特例。所谓年金，指的是在整个期限里，设为n年，每年支付固定数额的现金流，每次的现金流包含利息与部分本金的偿还。

假设年金每次支付额为C，每年m次，期限为n年，每年的折现率相同为r。如期末支付，则该年金的现值为多少？如期初支付，结果如何？

（1）如果支付发生在期末，年金的现值为：

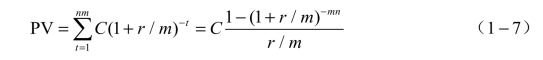
（2）永续年金（期末支付）：

（3）如果支付发生在期初：

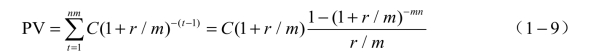
（4）如果支付发生在期末，年金的将来值为：

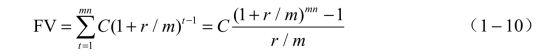
（5）如果支付发生在期初，年金的将来值为：

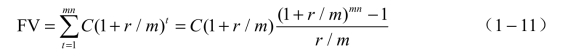
例1.5　如额度为200 000元，利率为6％的10年期房屋贷款，每月的还款额为多少？请计算每月还款额中归还的本金与利息各为多少？可以得到什么结论？

解：根据式（1-7）可以求出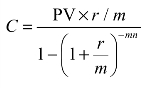，带入相关数据可以求出每月需要

归还的数额为：(www.xing528.com)

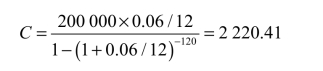
每个月需要归还的利息=本金×月利率=200 000×0.06/12=1 000元

第一个月归还本金=2 220.41-1 000=1 220.41

剩余本金=200 000-1 220.41=198 779.59

第二个月归还利息=198 779.59×0.06/12=993.90

第二个月归还本金=2 220.41-993.90=1 226.51

剩余本金=198 779.59-1 226.51=197 553.08

以此类推，我们可以求出所有贷款期限里每个月需要归还的本金与利息数。读者可以自行补充完成。显然本金的归还逐渐增加，利息的归还逐渐减少。

例1.6　有一个年龄为58岁的雇员将在63岁退休。他计划在退休前的5年内每年年初将一笔款存入一个年利率为10％的户头，并计划在退休后的10年内，每年年初从该户头提取15 000元用于消费。问现在每年应该存入多少钱进该账户可以达到要求？

解：我们可以把现金流的变化用图1-4表示出来。d表示前五年的存入金额，c表示从户头提取的15 000元。则根据题意，我们可以得到：

解出d=15 096.97元。

图1-4　各期现金流变化图