方差分析和列联分析的比较与应用

第八章　方差分析与列联分析

本章主要介绍在实践中应用非常广泛的两种统计分析方法:方差分析与列联分析。在方差分析部分，主要介绍方差分析的基本原理以及单因素方差分析的基本方法，无交互作用的双因素方差分析的基本方法。在列联分析部分，主要介绍拟合优度检验和独立性检验的方法。

第一节　方差分析的基本问题

方差分析从本质上讲，也是假设检验问题，是前述假设检验问题的拓展。在第六章中介绍了假设检验的一般原理，我们曾利用z统计量来判别样本均值与总体均值是否具有显著性差异。换句话说，也就是判别两个均值之间是否具有显著性差异。而本章所要介绍的方差分析则是要判断多个样本均值之间是否具有显著性差异，进而判断每个样本均值所对应的总体均值之间是否具有显著性差异，其检验效率更高。从形式上看，方差分析是比较多个总体的均值是否相等，但本质上它所研究的是变量之间的关系。方差分析是在20世纪20年代发展起来的一种统计方法，最早是用来判断施肥量和农作物产量之间关系的。目前，方差分析方法应用非常广泛，尤其是用于分析心理学、生物学、工程和医学的试验数据。

一、什么是方差分析

方差分析(analysis of variance，ANOVA)就是通过检验各总体的均值是否相等来判断分类型自变量对数值型因变量是否有显著影响。这里所讲的分类型自变量以及数值型因变量就是我们在第一章导论中曾经介绍过的分类型变量和数值型变量。

下面通过例题来说明方差分析的有关概念及其要解决的问题。

【例8－1】一个工程技术人员想要分析某企业机器操作员对企业所生产的阀门口径的影响，选择了4个不同的工人操作机器，从第一个工人所生产的产品中随机抽取5件产品，从第二个工人所生产的产品中随机抽取8件产品，从第三个工人所生产的产品中随机抽取7件产品，从第四个工人生产的产品中随机抽取4件产品，各操作人员生产的阀门口径资料如表8－1所示，试分析不同操作员所生产的产品质量是否存在显著差异。

表8－1　各操作员生产的阀门口径　　单位:厘米

在这个例子中，我们可以用前述的t检验方法进行两两检验，然后判断各个总体之间的差异，这样就需要做6次检验。对于每一个特定的检验，如果α= 0.05，那么，犯弃真错误的概率为5%，如果进行足够多次试验，则总会有一个或多个正确的原假设被拒绝，因此，只有在一次t检验的条件下，α= 0.05才成立。由于要进行6次t检验，因此犯弃真错误的可能性增大，这样，当分析人员做完全部检验后，实际上犯弃真错误的概率远大于0.05，本节介绍的方差分析则避免了这种错误概率的累积。

在这个例题中，如果把每一个工人所生产的全部产品看作是一个总体，有4个工人，所以，就有4个总体，这里的“工人”就是方差分析概念中所讲的分类型自变量，阀门口径就是方差分析概念中所讲的数值型因变量，要分析4个工人的产品质量是否有显著差异，实际上也就是判断“工人”这个分类型自变量对“阀门口径”这个数值型因变量是否有显著影响，要做出这种判断，可以将问题转化成4个工人所生产的阀门口径的均值是否有显著的差异。如果他们的均值没有显著差异，就意味着不同的操作者对产品的质量没有显著影响，也就是说，4个操作者在操作技术上没有显著差别;如果他们的均值有显著差异，则意味着4个工人所生产的产品质量存在着明显的差异。设μ1为第一个工人所生产产品的平均口径，μ2为第二个工人所生产产品的平均口径，μ3为第三个工人所生产产品的平均口径，μ4为第四个工人所生产产品的平均口径，可以将上述问题转化成检验下面的假设是否成立的问题，即

H0:μ1=μ2=…=μk　　自变量对因变量没有显著影响

H1:μI(i= 1，2，…，k)　　不完全相等，自变量对因变量有显著影响式中，μI为第i个总体的均值。

检验这个假设所采用的方法就是方差分析。

为了更好地叙述方差分析的一般理论，方差分析中把所要检验的对象称为因素或因子，因素的不同表现称为水平或处理。如上例中的要检验不同的操作人员对产品质量是否有影响，这里的操作人员就是因素，操作员1、操作员2、操作员3、操作员4就是操作人员这一因素的具体表现，称为水平或处理，从每个操作员所生产的产品中所抽取的样本数据称为观测值。

二、方差分析的基本思想

在例8－1中，检验不同的工人所生产的产品是否有显著差异的方法之所以称为方差分析，是因为虽然要检验的是均值是否具有显著性差异，但在判断均值之间是否具有差异时要借助于方差。由此可见，这种方法是通过对数据误差来源的分析来判别不同总体的均值是否相等，进而分析自变量对因变量是否具有显著影响，因此，进行方差分析时，需要分析数据误差的来源。

1．误差来源

方差分析是通过对数据误差的分解来进行分析的。在方差分析中将数据误差分为两类:随机误差和组间误差。随机误差是指在因素的同一水平(同一个总体，即例题8－1中同一个操作人员)下，样本的各观测值之间的差异。在例8－1中，从同一个操作员所生产的阀门中抽取若干件产品，其质量参数值(阀门口径)也是不相同的，这种误差可以看成是随机因素的影响，或者说是由于抽样的随机性造成的，即随机误差，也称为组内误差。组间误差是指在因素的不同水平(不同总体，即例题8－1中不同的操作人员)下，各观测值之间的差异。在例8－1中，各个操作员的产品质量参数也是有差异的。这种误差可能是由于抽样本身形成的随机误差，也可能是由于不同的操作员本身的系统性(技术差异)因素所造成的系统误差，因此，组间误差是随机误差和系统误差的总和。

在方差分析中，数据的误差是用各变量值与相应均值的离差平方和来表示的，否则，数据的误差无法量化，无法进一步分析。

反映组内误差大小的平方和称为组内平方和，也称为误差项平方和或残差平方和，记为SSE。反映组间误差大小的平方和称为组间平方和，记为SSA，这两类误差的计算过程将在本章第二节中论述。

2．误差分析

如果各个工人的技术水平相同，那么在组间误差中只包含随机误差，而没有系统误差，这时，组间误差与组内误差经过平均后的数值(称为均方或方差，平均的原因主要是为了消除样本容量大小对误差的影响)就应该很接近，它们的比值就会接近于1;反之，如果不同工人对产品的质量参数有影响，在组间误差中除了包含随机误差，还会包含系统误差，这时，组间误差平均后的数值会大于组内误差平均后的数值，它们之间的比值会大于1，当这个比值大到某种程度时，就认为因素的不同水平之间存在着显著差异，也就是自变量对因变量有显著影响。因此，判断不同工人所生产的产品质量有没有明显差异这一问题，实际上也就是检验产品质量的差异究竟是由什么原因引起的，如果这种差异主要是系统误差，就认为不同的工人对产品质量有影响。在方差分析的假定前提下，要检验不同工人对产品质量是否有影响在形式上也就转化为检验4个工人所生产的产品的均值是否相等的问题。

3．方差分析的基本假定方差分析有3个基本假定:

(1)每个总体都服从正态分布。也就是说，对于因素的每一个水平，其观测值是来自正态分布总体的简单随机样本。在上例中，要求每个工人所生产产品的质量参数都服从正态分布。

(2)各个总体的方差σ2必须相同。也就是说，对于各组观察数据，是从具有相同方差的正态总体中抽取的。

(3)观测值是独立的。如在上例中，要求每个被抽中的工人所生产的产品质量参数都与其他工人的产品质量参数是独立的。

在上述假定成立的条件下，要分析自变量对因变量是否有影响，形式上也就转化为检验自变量的各个水平(总体)的均值是否相等。例如，判断不同工人对产品质量是否有影响，实际上也就是检验具有相同方差的4个正态总体的均值(阀门口径均值)是否相等。

尽管不知道4个总体(每个工人所生产的全部产品)的均值，但可以利用样本数据来检验它们是否相等，如果4个总体的均值相等，可以期望4个样本的均值也会很接近。事实上，4个样本的均值越接近，推断4个总体均值相等的证据也就越充分;反之，样本均值越不同，推断总体均值不同的证据就越充分。换句话说，样本均值变动越小，越支持H0;样本均值变动越大，越支持H1。如果原假设H0:μ1=μ2=μ3=μ4(4个工人产品的均值相等)为真，则意味着每个样本都来自均值为μ，方差为σ2的同一个正态总体。由样本均值的抽样分布可知，来自正态总体的一个简单随机样本均值珋x服从均值为μ、方差为σ2/n的正态分布。如果μ1，μ2，μ3，μ4完全不同，则意味着4个样本分别来自均值不同的4个正态总体，因此有4个不同的抽样分布。

方差分析按照涉及的分类型自变量的多少，可以分为单因素方差分析和多因素方差分析。当方差分析中只涉及一个分类型自变量时，称为单因素方差分析;当方差分析中涉及两个分类型自变量时，称为双因素方差分析。

第二节　单因素方差分析

单因素方差分析研究的是一个分类型自变量对一个数值型因变量的影响。如上例中，要检验不同的操作者对产品质量是否有显著影响，这里的操作者就是分类型自变量，产品质量参数就是数值型因变量。再例如，检验饮料的颜色对饮料的销量是否有影响，检验某一品牌的手机在不同的地区销量是否有显著差异，这里饮料的颜色、手机的销售地区就是分类型自变量。这些检验中，影响因变量的因素只有一个，所以属于单因素方差分析。本节先介绍单因素方差分析。

一、单因素方差分析的数据结构

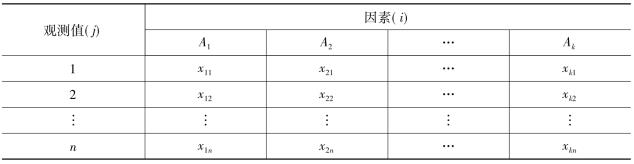
进行单因素方差分析，需要得到下面的数据结构，如表8－2所示。

在单因素方差分析中，用A表示因素，因素的k个水平(总体)分别用A1，A2，…，Ak表示，每个观测值用xij(i= 1，2，3，…，k，j= 1，2，3，…，n)表示，即xij表示第i个水平(总体)的第j个观测值，如x21表示第二个水平的第一个观测值，等等。其中从不同水平中所抽取的样本容量可以相等，也可以不相等。

表8－2　单因素方差分析数据结构

二、单因素方差分析的步骤

为检验自变量对因变量是否有显著影响，首先需要提出“分类型自变量对数值型因变量没有显著影响”的原假设，然后构造一个统计量来检验这一假设是否成立，与第六章介绍的假设检验的步骤相同。方差分析包括提出假设、构造检验统计量、统计决策等步骤。

1．提出假设

在方差分析中，原假设是分类型自变量对数值型因变量没有影响。在例8－1中，也就是假设不同的操作人员对产品质量参数没有影响，因此，原假设和备择假设的一般形式如下:

H0:μ1=μ2=…=μk　　即自变量对因变量没有显著影响

H1:μI(i= 1，2，3，…，k)不全相等　即自变量对因变量有显著影响

式中，μi为第i个总体的均值。

如果拒绝原假设H0，则意味着自变量对因变量有显著影响，也就是自变量与因变量之间有显著关系，在例8－1中，也就是不同的操作人员对产品质量有影响;如果接受原假设H0，则表明自变量对因变量没有显著影响，也就是说，不能认为自变量与因变量之间有显著关系，在例8－1中，也就是不同的操作人员对产品质量没有影响。

2．构造检验统计量

为检验H0是否成立，需要确定检验的统计量。如何构造这一统计量呢?在此结合表8－1的资料进行说明。

第一，计算各样本的均值。假定从第i个总体中抽取一个容量为n的简单随机样本，令珋xi为第i个总体的样本均值，则有

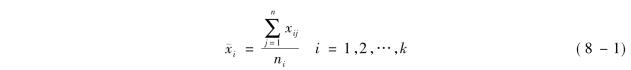
式中，ni为第i个总体的样本容量，xij为第i个总体的第j个观测值。例如根据表8－1中的数据计算第一个操作者的均值为

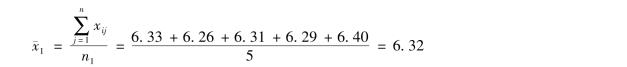
同样可以计算出第二、第三、第四个操作者的样本均值，结果见表8－3的最后一行。

表8－3　4个工人产品质量参数及均值

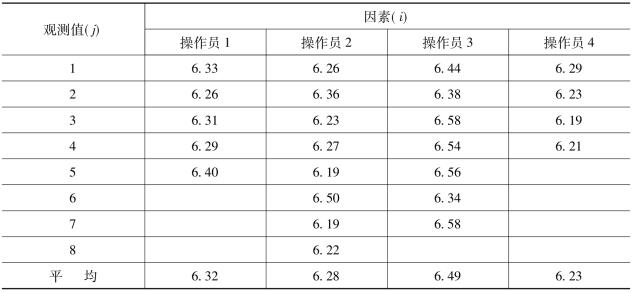
第二，计算全部观测值的总均值:

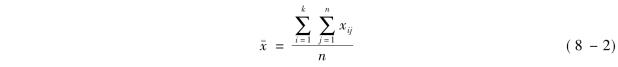
例如根据表8－1中的数据计算所有观测值的均值为:

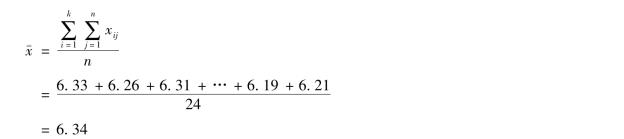
第三，计算各误差的平方和。为构造检验统计量，在方差分析中需要计算组间误差平方和(因素平方和)SSA、组内误差平方和(或称残差平方和)SSE。

组间平方和，记为SSA，它是各组均值珋xi与总均值珌x的误差平方和，反映各样本均值之间的差异程度，又称为因素平方和，其计算公式为

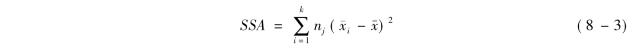
结合表8－1及表8－3资料利用式(8－3)计算的组间平方和如下:

组内平方和，记为SSE，它是每个水平或组的各样本数据与其组均值的误差平方和，反映了每个样本各观测值的离散状况，因此称为组内平方和。该平方和反映了随机误差的大小，其计算公式为

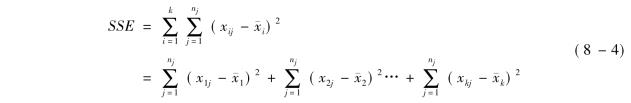
上述公式的第二步其实就是每个操作者的质量参数与其均值的误差平方和，然后将每个操作者的误差平方和加总，即为误差项平方和。在例8－1中，其实就是4个操作者误差项的平方和，分别为

操作者1的误差平方和为

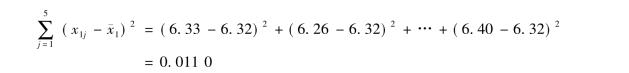
操作者2的误差平方和为

操作者3的误差平方和为

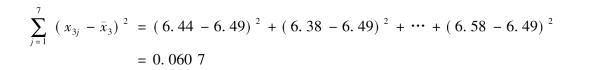
操作者4的误差平方和为

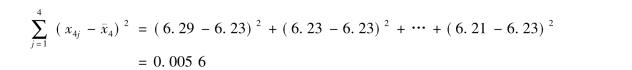
误差项平方和为

SSE= 0.011 0+ 0.077 5+ 0.060 7+ 0.005 6= 0.154 9

以上分别计算了组间误差平方和SSA以及随机项误差平方和SSE，SSA是对随机误差和系统误差大小的度量，它反映了自变量(不同的操作者)对因变量(阀门口径)的影响，也称为自变量效应或因子效应;SSE是对随机误差大小的度量，它反映了除自变量对因变量的影响之外，其他因素对因变量的总影响，因此，SSE也被称为残差变量，它所引起的误差也称为残差效应。

第四，计算统计量。由于各误差平方和的大小与观测值的多少有关，为了消除观测值多少对误差平方和大小的影响，需要将其平均，也就是用各平方和除以它们所对应的自由度，这一结果称为均方，也称为方差。以上两个平方和所对应的自由度分别为:SSA的自由度为k －1，其中k为因素水平(总体)的个数。SSE的自由度为n－k。

由于要比较的是组间均方和组内均方之间的差异，所以通常只计算SSA的均方和SSE的均方，SSA的均方也称为组间均方或组间方差，记为MSA，其计算公式为

以例8－1为例，计算的组间方差为

SSE的均方也称为组内均方或组内方差，记为MSE，其计算公式为

以例8－1为例，计算的组内方差为

将MSA和MSE进行对比，就得到所需要的检验统计量F。当H0为真时，二者的比值服从分子自由度为k－1，分母自由度为n－k的F分布，即

以例8－1数据来计算的F统计量为

3．统计决策

如果原假设H0:μ1=μ2=…=μk成立，则表明没有系统误差，组间方差MSA与组内方差MSE的比值差异就不会太大，如果组间方差显著大于组内方差，说明各水平(总体)之间的差异显然不仅仅有随机误差，还有系统误差。用例8－1来说，如果不同的操作者对阀门质量参数没有影响，也就是说4个工人的技术水平差异不大，那么，4个工人产品质量参数的均值之间的差异与每个操作者质量参数的内部差异相比，二者就不会相差很大;反之，则意味着不同的操作者对产品质量有影响。可见，判断因素的水平是否对其观测值有显著影响，实际上也就是比较组间方差与组内方差之间差异的大小。那么，它们之间的差异大到何种程度才表明有系统差异存在呢?这就需要用检验的统计量进行判断，将统计量的值F与给定的显著性水平α的临界值Fα进行对比，从而做出对原假设H0的决策。

根据给定的显著性水平α，在F分布表中查找与分子自由度d f= k－1，分母自由度d f= n－k相应的临界值Fα(k－1，n－k)。

若F＞Fα，则拒绝原假设H0:μ1=μ2=…=μk，表明μi(i= 1，2，3，…，k)之间的差异是显著的。也就是说，所检验的因素(不同的操作者)对观测值(阀门口径)有显著影响。

若F＜Fα，则接受原假设H0，没有证据表明μi(i= 1，2，3，…，k)之间有显著差异。也就是说，这时还不能认为所检验的因素(不同的操作者)对观测值(阀门口径)有显著影响。

以例8－1的资料，F= 10.12，如果给定显著性水平α= 0.05，查分子自由度为3，分母自由度为20的F分布表，得到F0.05(3，20)= 3.10，所以有F= 10.12＞F0.05= 3.10，因此拒绝原假设，因此，不同机器操作员生产的阀门口径的均值之间有显著差异。

4．方差分析表

上面详细介绍了方差分析的计算步骤和计算过程，为使计算过程更加清晰，通常将上述过程的内容列在一张表内，这就是方差分析表，其一般形式如表8－4所示。

表8－4　方差分析表的一般形式

将例8－1的计算结果用方差分析表的形式表示出来，如表8－5所示。

表8－5　4个操作者所生产产品质量参数方差分析表

三、关系强度的测定

例8－1的方差分析结果表明，不同操作者质量参数的均值之间有显著差异，这意味着操作者(自变量)与质量参数(因变量)之间的关系是显著的。表8－5中给出了组间平方和(组间SS)，它度量了自变量(操作者)对因变量(质量参数)的影响效应。实际上，只要组间平方和(组间SS)不等于0，就表明两个变量之间有关系(只是是否显著的问题)。当组间平方和比组内平方和(组内SS)大，而且大到一定程度时，就意味着两个变量之间的关系显著，大得越多，表明它们之间的关系越强;反之，当组间平方和比组内平方和小时，就意味着两个变量之间的关系不显著，小得越多，表明它们之间的关系就越弱。那么，怎样度量它们之间的关系强度呢?可以用组间平方和(SSA)占总平方和(SST，总平方和SST=组间平方和+组内平方和= SSA+ SSE，在例8－1中，SST= SSA+ SSE= 0.237+ 0.155= 0.392)的比例大小来反映，这一比例记为R2，即

其平方根R就可以用来测量两个变量之间的关系强度。

例如，根据表8－5中的计算结果得

这表明操作者(自变量)对质量参数(因变量)的影响效应占总效应的60.4%，而残差效应占39.6%，也就是说，不同的操作者对质量参数差异解释的比例达到60.4%，而其他因素(残差变量)所解释的比例为39.6%以上。

R2的平方根(类似于第七章中介绍过的相关系数r)可以用来测量自变量与因变量之间的关系强度，例如，根据上面的结果可以计算出R= 0.777，这表明，操作员的技术水平与产品质量参数显著相关。

四、方差分析中的多重比较

用方差分析检验k个总体的均值是否相等时，拒绝原假设只能得出总体均值不全相等的结论，此时我们需要进一步检验并判定哪些均值之间存在差异。通过对例8－1的分析结果，得出的结论是:不同操作者产品质量参数的均值是不相同的，但究竟哪些均值之间不相等呢?这种差异到底出现在哪些操作者之间呢?也就是说，μ1与μ2、μ1与μ3、μ1与μ4、μ2与μ3、μ2与μ4、μ3与μ4之间究竟是哪两个均值不同呢?这就需要做进一步的分析，所使用的方法就是多重比较方法，它是通过对总体均值之间的配对比较来进一步检验到底哪些均值之间存在差异。

多重比较的方法有许多种，这里介绍的是由费希尔提出的最小显著差异方法，缩写为LSD。

第一步，提出假设:

H0:μi=μj，H1:μi≠μj

第二步，计算检验统计量:。

第三步，计算LSD，其公式为式中，tα/2为t分布的临界值，通过查t分布表得到，其自由度为(n－k)，这里的k是因素中水平的个数;MSE为组内方差;ni和nj分别为第i个样本和第j个样本的样本量。

第四步，根据显著性水平α做出决策，如果|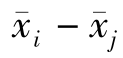|＞LSD，则拒绝H0;如果|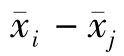|＜LSD，则不拒绝H0。

【例8－2】根据表8－5中4种方差分析的结果，对4个操作员产品质量参数做多重比较(α= 0.05)。

第一步，提出假设:

H0:　μ1=μ2，μ1=μ3，μ1=μ4，μ2=μ3，μ2=μ4，μ3=μ4

H1:　μ1≠μ3，μ1≠μ3，μ1≠μ4，μ2≠μ3，μ2≠μ4，μ3≠μ4

第二步，计算检验统计量:

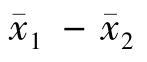||=| 6.32－6.28|= 0.04

||=| 6.32－6.49|= 0.17

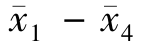||=| 6.32－6.23|= 0.09

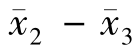||=| 6.28－6.49|= 0.21

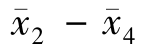||=| 6.28－6.23|= 0.05

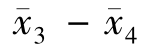||=| 6.49－6.23|= 0.26

第三步，根据表8－5资料，计算LSD的值，如果各个操作员的样本容量相同，只需要计算一个LSD的值，但在例8－1中，由于样本容量不同，所以需要分别计算LSD，在自由度n－k= 24－4= 20，α= 0.05，查t分布表得临界值tα/2= t0.025= 2.086，计算如下:检验μ1=μ2时的

检验μ1=μ3时的

检验μ1=μ4时的

检验μ2=μ3时的

检验μ2=μ4时的

检验μ3=μ4时的

第四步，决策。

因为|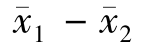|= 0.04＜0.104 7，所以接受原假设，也就是说第一个操作员和第二个操作员的产品质量没有显著差异。

因为|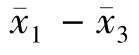|= 0.17＞0.107 5，所以拒绝原假设，也就是说第一个操作员和第三个操作员的产品质量有显著差异。

因为|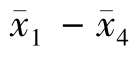|= 0.09＜0.123 2，所以接受原假设，也就是说第一个操作员和第四个操作员的产品质量没有显著差异。

因为|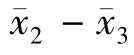|= 0.21＞0.095 0，所以拒绝原假设，也就是说第二个操作员和第三个操作员的产品质量有显著差异。

因为|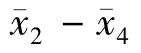|= 0.05＜0.112 4，所以接受原假设，也就是说第二个操作员和第四个操作员的产品质量没有显著差异。

因为|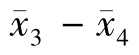|= 0.26＞0.115 1，所以拒绝原假设，也就是说第三个操作员和第四个操作员的产品质量有显著差异。

第三节　双因素方差分析

一、双因素方差分析的概念

双因素方差分析是同时分析两个分类型自变量对数值型因变量是否有显著影响的分析方法。

单因素方差分析只是考虑一个分类型自变量对数值型因变量的影响，在对实际问题的研究中，有时需要考虑几个因素对试验结果的影响。例如，分析影响彩电销售量的影响因素时，需要考虑品牌、销售地区、价格、质量等多个因素的影响;分析电脑的销售量时，不同的营销方法、不同的地区都是影响电脑销售量的因素等。当方差分析中涉及两个分类型自变量时，称为双因素方差分析。

【例8－3】有4个品牌的手机在4个地区销售，为了分析手机的品牌(“品牌”因素)和销售地区(“地区”因素)对销量的影响，对每个品牌在各地区的销售量取得如下数据(单位:部)，如表8－6所示(α= 0.05)。

表8－6　手机销售资料　　单位:部

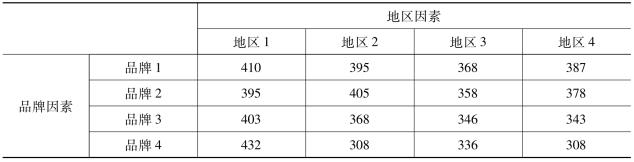
在上面的例子中，品牌和地区是两个分类型自变量，销售量是一个数值型因变量，同时分析品牌和销售地区对销售量的影响，分析究竟是一个因素在起作用，或是两个因素都起作用，这就是一个双因素方差分析问题。

为了分析的方便，在双因素方差分析中，把排在列位置的因素称为列因素，如例8－3中的“地区”;把排在行位置的因素称为行因素，如例8－3中的“品牌”。由于有两个影响因素，如果两个分类型自变量(因素)对因变量的影响是相互独立的，分别判断行因素和列因素对数据的影响，这时的双因素方差分析称为无交互作用的双因素方差分析。如果除了行因素和列因素对试验数据的影响外，两个因素的搭配还会对结果产生一种新的影响，这时的双因素方差分析称为有交互作用的双因素方差分析或可重复双因素方差分析。例如，手机的“品牌”因素和“地区”因素，如果这两个因素对销售量的影响作用是相互独立的，分别判断“品牌”因素和“地区”因素对销售量的影响，这时的双因素方差分析称为无交互作用的双因素方差分析;如果除了“品牌”因素和“地区”因素对销售量的单独影响外，两个因素的搭配还会对销售量产生一种新的影响效应，例如，某个地区对某个品牌的手机有特殊偏好，这就是两个因素结合后产生的新效应，这时的双因素方差分析称为有交互作用的双因素方差分析，或称为可重复双因素方差分析。本节主要介绍无交互作用的双因素方差分析。

双因素方差分析的基本假定与单因素方差分析相同。

二、双因素方差分析的数据结构

前已述及，在双因素方差分析中，有两个因素，将一个因素安排在“行”的位置，称为行因素;另一个安排在“列”的位置，称为列因素。设行因素有k个水平，行1，行2，…，行k(如例8－3中的品牌1，品牌2，品牌3，品牌4)，列因素有r个水平，列1，列2，…，列r(如例8－3中的地区1，地区2，地区3，地区4)。行因素和列因素的每一个水平都可以搭配成一组。

表8－7中，每一个观察值xij(i= 1，2…，k，j= 1，2，…，r)看作是由行因素的k个水平和列因素的r个水平所组合成的kr元素的总体中抽取的样本容量为1的简单独立随机样本，其中，每一个总体都服从正态分布且有相同的方差。

表8－7　双因素方差分析的数据结构

表8－7中的珋xi是行因素第i个水平下各观察值的均值，即

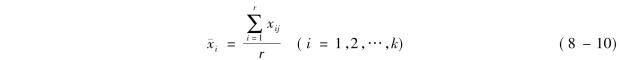
是列因素第j个水平下各观察值的均值，即:

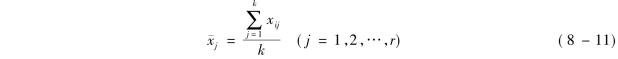
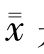是全部kr各观察值的均值，即

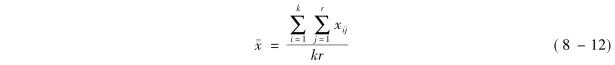
三、双因素方差分析的步骤

前已述及，方差分析从本质上讲，也是一个假设检验问题，双因素方差分析也包括提出假设、确定检验统计量、决策分析等步骤。

1．提出假设

本节只介绍无交互作用的双因素方差分析，所以只需检验两个独立因素对因变量的影响，需要对两个因素分别提出如下假设:对行因素提出的假设为

H0:μ1=μ2=…=μk行因素(自变量)对因变量没有显著影响

H1:μi(i= 1，2，…，k)不完全相等，行因素(自变量)对因变量有显著影响式中，μi为行因素第i个水平的均值。对列因素提出的假设为

H0:μ1=μ2=…=μr列因素(自变量)对因变量没有显著影响

H1:μj(j= 1，2，…，r)不完全相等，列因素(自变量)对因变量有显著影响式中，μj为列因素第j个水平的均值。

2．构造检验统计量

为了检验H0是否成立，需要分别确定检验行因素和列因素的统计量。为此，需要从总误差平方的分解入手，这里进行的是无交互作用的双因素方差分析，需要分别确定检验行因素和列因素的统计量，只不过这里多了一个因素而已，需要计算的误差平方和也会多一个。

首先需要计算总误差平方和。总误差平方和是全部观察值xij与总平均值珌x的误差平方和，计算过程如下:

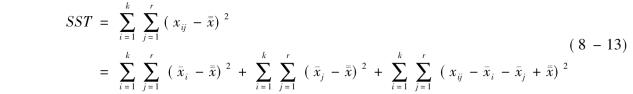
从总误差平方和的公式中可以看出，总误差平方和可分解为3项。下面分别对这3项进行解释。第一项是行因素所产生的误差平方和，记为SSR，即

第二项是列因素所产生的误差平方和，记为SSC，即

第三项是除行因素和列因素影响之外的剩余因素影响产生的误差平方和，称为随机误差平方和，记为SSE，即

上述3个平方和的关系是

在上述误差平方和的基础上，需要将各误差平方和除以各自的自由度，其结果叫称为均方，也就是将各平方和除以相应的自由度，与各误差平方和相对应的自由度分别为:

总误差平方和SST的自由度为kr－1;

行因素的误差平方和SSR为k－1;

列因素误差平方和SSC的自由度为r－1;

随机误差平方和SSE的自由度为(k－1)×(r－1)。

为构造检验统计量，需要计算下列各均方:

行因素的均方，记为MSR，即

列因素的均方，记为MSC，即

随机误差项的均方，记为MSE，即

检验行因素对因变量的影响是否显著，构造的统计量为

检验列因素对因变量的影响是否显著，构造的统计量为

3．统计决策

计算出检验的统计量后，根据给定的显著性水平α和两个自由度，查F分布表得到相应的临界值Fα，然后将Fα和FR与FC进行比较。

如果FR＞Fα，拒绝原假设H0:即μ1=μ2=…=μk不成立，表明μi(i= 1，2，…，k)之间的差异是显著的，也就是说，所检验的行因素对观测值有显著影响。

如果Fc＞Fα，拒绝原假设H0:即μ1=μ2=…=μr不成立，表明μj(i= 1，2，…，r)之间的差异是显著的，也就是说，所检验的列因素对观测值有显著影响。

上面讨论了双因素方差分析的计算步骤和过程，为使计算过程更加清晰，通常将上述过程的内容列成方差分析表，其一般形式如表8－8所示。

表8－8　无交互作用的双因素方差分析表

为了便于理解，下面以表8－6的资料来说明无交互作用的双因素方差分析。

(1)对两个因素分别提出以下的假设。

对行因素提出的假设为

H0:μ1=μ2=…=μk品牌因素(自变量)对因变量没有显著影响

H1:μi(i= 1，2，…，k)不完全相等，品牌因素(自变量)对因变量有显著影响

式中，μi为行因素第i个水平的均值。

对列因素提出的假设为

H0:μ1=μ2=…=μr地区因素(自变量)对因变量没有显著影响(www.xing528.com)

H1:μj(j= 1，2，…，r)不完全相等，地区因素(自变量)对因变量有显著影响

式中，μj为列因素第j个水平的均值。为了构造统计量，首先要计算行因素的均值和列因素的均值，计算结果如表8－9所示。

表8－9　双因素方差分析的均值计算表

(2)构造检验统计量。

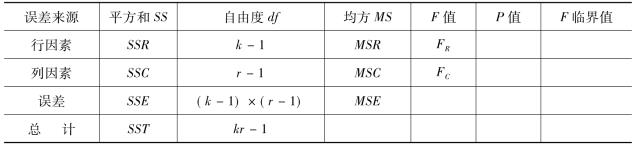
需要计算行因素所产生的误差平方和SSR，列因素所产生的误差平方和SSC，剩余因素影响产生的误差平方和SSE，结合表8－9的资料计算如下:

其中第一项:

第二项:

第三项:

第四项:

代入数字，可求得

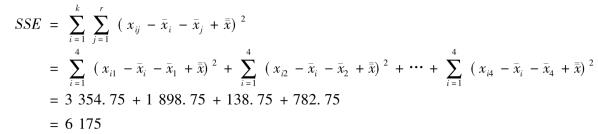
下面计算均方。

行因素的均方，记为MSR，公式为(8－19)，即

列因素的均方记为MSC，公式为(8－20)，即

随机误差项的均方记为MSE，即

检验行因素对因变量的影响是否显著，构造的统计量为:

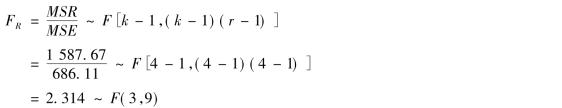
检验列因素对因变量的影响是否显著，构造的统计量是:

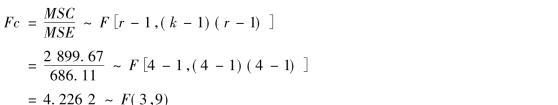
(3)决策

在α= 0.05的条件下，由于本例中的检验行因素和列因素的自由度相等，所以，临界值也一样(特别强调，如检验行因素的自由度与检验列因素的自由度不相等，则检验行因素和列因素的临界值就不同)，查教材后所附的F分布表得临界值得Fα= 3.86。

因为FR= 2.314＜Fα= 3.86，所以接受原假设，也就是在本例中，品牌因素对销售量没有显著影响;因为Fc= 4.226 2＞Fα= 3.86，所以拒绝原假设，也就是在本例中，地区因素对销售量有显著影响。四、关系强度的测量

同单因素方差分析中关系强度的衡量方法一样，也可以从误差平方和的分解入手，方差分析中给出了总误差平方和、行自变量误差平方和、列自变量误差平方和和误差项平方和。很明显，我们可以用行平方和度量品牌这个自变量对因变量的影响效应，列平方和度量地区这个自变量对因变量(销售量)的影响效应，这两个平方和加在一起度量两个自变量对因变量的联合效应，联合效应与总平方和的比值定义为R2，其平方根R反映了这两个自变量量联合起来与因变量的关系强度，即

例如，根据上述计算结果得到

这表明，品牌因素和地区因素联合起来总共解释了销售量差异的68.554%，其他因素(参差变量)解释了销售量差异的31.446%。而R= 82.8%表明了品牌和地区两个因素结合起来与销售量之间的关系。当然，也可以分别考察品牌和地区与销售量之间的关系，这就需要做每个自变量与销售量的单因素方差分析，并分别计算每个R2进行分析。

第四节　列联分析

本节所介绍的方法主要用于两类分析，即独立性分析和拟合优度分析，主要用于分析分类型自变量。

一、列联表

列联分析是通过列联表进行分析。所谓列联表，是指由两个以上的变量进行交叉分类的频数分布表。例如，假如饭店经理希望了解就餐者的年龄与就餐时所点饮料类型有没有关联，在一份调查问卷中，用下面两个问题来测量:

你的年龄?

a．35岁以下　b．35～55　c．55以上

你所偏爱的饮料?

a．咖啡/茶　b．软饮料　c．其他(牛奶等)随机抽取了309位在饭店就餐的顾客，整理成如表8－10所示的表格。

表8－10　消费者年龄与饮料资料

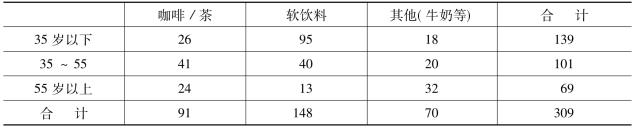
表8－10就是列联表，像这样的表格在实践中经常能见到。列联分析本质上也是一个假设检验问题，对列联表的分析分为拟合优度分析或称拟合优度检验和独立性分析或称独立性检验。先介绍拟合优度检验问题，例如，某公司实行三班制的值班制度，公司经理希望了解3个班组的产品质量是否存在差异，他从昨天生产的全部产品中抽出584个零部件进行检验，所得的结果如表8－11所示。

表8－11　某公司3个班组生产情况

在列联表中，排列在行的变量称为行变量，这里分为两类:合格品和不合格品。排列在列的变量称为列变量，这里分为3类:早班、中班、晚班。

二、列联分析的步骤

第一步;计算列联表中观察值的分布与期望值分布。

事实上，表8－11就是一个观察值分布，表的最右边显示了产品的总数，如合格品为500件，不合格品为84件，对此称为行边缘频数;表的最下边显示了单位变量总数，如3个班组的产品分别为168件、184件、232件，对此称为列边缘频数。这样，列联表所表现的就是在X条件下变量Y的分布，或者在变量Y条件下变量X的分布，因此又把列联表中的观察值分布称为条件分布，每个具体的观察值就是条件频数，如早班的190件产品就是条件频数。条件频数反映了数据的分布，但是不适合对比。例如，早班的合格品有190件，中班的合格品有160件，但是，仅据此不能说早班的合格率更高一些，因为早班的产品总数多，中班的产品总数少，它们对比的基数不同，为了能够在相同的基数上进行对比，使列联表中的数据提供更多的信息，可以计算相应的百分比，如表8－12所示。

表8－12　包含百分比的列联表

表中主栏的每个单元中有4个数据，各数据的含义是条件频数、行百分数、列百分数、总百分数。例如，第一个单元(早班合格品数)中第一个数字190为观察值频数;第二个数字38为行百分数，即190/500= 0.38或38%，第三个数字81.9为列百分数，即190/232= 0.819或81.9%，第四个数字32.5为总百分数，即190/584= 0.325或32.5%。在最右边的一栏中各有两行数字，第一行是行边缘频数和行边缘频数的百分比，如500= 190+ 160+ 150，85.6%= 500/584，同样84= 42+ 24+ 18，14.4%= 84/554，最下边的两行数字分别是列边缘频数和列边缘频数的百分比。为了对列联表进行更进一步的分析，还必须计算期望值的分布。什么是期望值分布呢?从逻辑上讲，在全部584个产品中，合格品有500件，占总数的85.6%，如果各个班组的产品质量没差异，那么，对于早班来说合格品就应当为232×0.856= 199件，中班的合格品就应当为184×0.856= 158件，晚班的合格品就应当为168×0.856= 144件，这里的199件、158件、144件就是本例中的期望值，由此可以计算出期望值的分布，如表8－13所示。

表8－13　期望值分布表

表8－14　观察值和期望值频数对比分布表

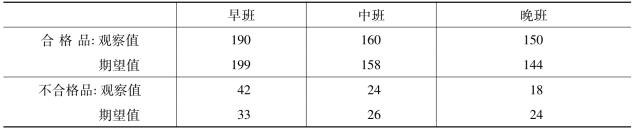
如果各个班组加工产品的质量没有明显差异，就应有π1=π2=π3= 0.856(这里的πi为第i个班组的合格率，π1=π2=π3= 0.856就是本例中的原假设，即3个班组的产品质量没有显著差异)，观察值和期望值就应当非常接近，对于π1=π2=π3= 0.856的原假设，可以采用χ2分布进行检验。χ2检验首先要计算χ2统计量。

第二步，计算χ2统计量。χ2统计量的计算公式如下:

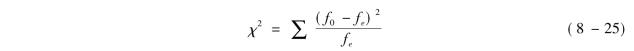
式中，f0表示观察值频数; fe表示期望值频数，以表8－14资料计算的χ2值如表8－15所示。

表8－15　χ2统计量计算表

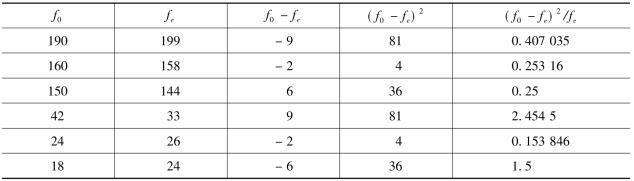
根据式(8－25)计算的χ2统计量如下:

现在回到前面所举的某公司的产品质量问题。如果3个班组的产品质量没有明显差异，那么，3个班组各合格率就应当是一样的，都等于85.6%;反之，如果这些比例不一致，表明3个班组的产品质量存在明显的差异。

第三步，根据给定的显著性水平和自由度查临界值。

这里显著性水平α取0.1，χ2分布中自由度=(行数－1)(列数－1)。本例中，自由度= (2－1)(3－1)= 2，在自由度为2的条件下，查χ2分布表的临界值为4.605 2。

第四步，决策。由于χ2＞χ2α= 4.605 2，故拒绝原假设，即认为3个班组的产品质量有明显的差异。

上面这个例题使用列联表进行拟合优度检验。所谓拟合优度检验就是要检验总体是否服从某个理论分布，它将总体分布中各个类的期望或理论频数与一个分布的观测频数做比较，其目的是分析观察数据与一组期望数据的拟合程度。同样地，拟合优度检验还可以检验某个样本资料是否服从均匀分布、正态分布，等等。

下面再介绍根据列联表进行独立性检验的问题。所谓独立性检验就是要检验两组资料是否存在相互关系，是对两个分类变量的频数进行分析，从而判定两个变量间是否独立的统计检验，这种分析在现实经济生活中应用很普遍。例如，一个市场分析人员可能希望了解消费者偏爱的软体饮料的类型与消费者的年龄是否相互独立，一个组织的行为研究人员可能希望了解缺勤率与工作类型是否相互独立，金融投资者可能希望了解优先股投资的类型与投资者所在的地区是否相互独立，等等。下面我们根据表8－10的资料来进行独立性分析。

第一步，提出假设。在表8－10中，假设如下:

H0:顾客喜欢的饮料类型与年龄无关

H1:顾客喜欢的饮料类型与年龄有关

第二步，计算统计量。这里统计量的计算仍然根据前面的χ2统计量的计算公式，为此，需要计算期望值频数，计算过程如下:在表8－10中，第一行35岁以下顾客所消费的饮料合计数为139，用139/309作为35岁以下顾客饮料比例的估计值。第一列，咖啡的消费量合计数为91，用91/309作为咖啡饮料的估计值，根据独立事件概率乘法公式，我们可以用下面的公式计算35岁以下并且消费咖啡饮料的顾客所占比例的期望值:

P(35岁以下，咖啡饮料)

　= P(35岁下)P(咖啡饮料)

　=(139/309)×(91/309)

　= 0.132 477

由此计算得出年龄在35岁以下且消费咖啡饮料的顾客的期望频数为0.132 477×309= 40.94。同样地，我们还可以计算出年龄在35～55岁之间且消费咖啡饮料顾客所占比例的期望概率为

P(年龄在35～55岁之间，咖啡)

　= P(年龄在35～55岁之间)P(咖啡)

　=(101/309)×(91/309)

　= 0.09626

由此计算得出年龄在35～55岁之间且消费咖啡饮料的顾客的期望频数为0.096 26 ×309= 29.74，我们把表8－10其他各单元的期望值频数及观察值频数一并列表如表8－16所示。

表8－16　观察值频数与期望值频数表

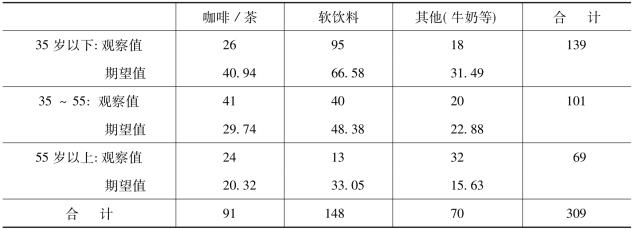
根据前述χ2统计量的计算公式，得到χ2统计量为

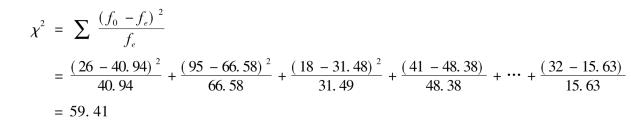
在显著性水平α= 0.01，自由度=(行数－1)(列数－1)=(3－1)(3－1)= 4的条件下，查表得临界值= 13.277。

第三步，决策。由于χ2统计量大于临界值，所以拒绝原假设。

拒绝原假设的意义是饮料类型与年龄不独立，顾客就餐时的饮料与年龄有关，观察各类可以发现，年轻人更喜欢软饮料，年纪大的人则更喜欢其他类型的饮料，餐饮业的管理人员和饮料推销员可以利用这些信息确定市场，从而提供适用的产品。

第五节　运用Excel进行方差分析

由上面介绍的方差分析过程可以看到，进行方差分析需要大量的计算工作，用手工计算是十分繁琐的，在实践中这些计算工作可以由计算机来完成。目前的统计软件中都有现成的方差分析程序，只要理解方差分析的基本原理，就可以对计算机输出的结果进行合理的解释和分析。在这里，利用熟悉的Excel软件结合例8－1及例8－3的数据，给出用Excel进行方差分析的步骤和结果。

一、利用Excel进行单因素方差分析

第一步，将操作员1的数据输入到A1单元格到A5单元格，将操作员2的数据输入到B1单元格到B8单元格，将操作员3的数据输入到C1单元格到C7单元格，将操作员4的数据输入到D1单元格到D4单元格。

第二步，选择“工具”下拉菜单，选择“数据分析”选项，然后单击“确定”。

第三步，在分析工具中选择“单因素方差分析”，然后单击“确定”。当对话框出现时，在“输入区域”方框中输入数据单元区域A1:D8，在［α］输入0.05(可根据需要确定)。在“输出选项”中选择输出区域，单击“确定”后，得到如表8－17所示的输出结果。

表8－17　单因素方差分析的输出结果

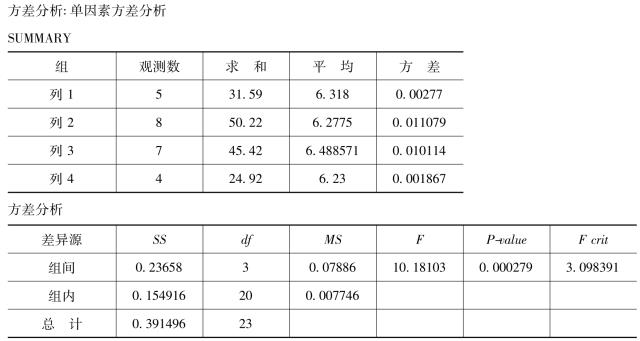
在表8－16中，“SUMMARY”部分是一些描述性的统计量，方差分析部分:“SS”表示平方和，“df”表示自由度，“MS”表示均方，“F”表示F检验的统计量，“P-value”表示用于检验的“P值”，“crit”为置信水平的α临界值。

二、利用Excel进行双因素方差分析

第一步，将例8－3种数据输入到A1:D4。

第二步，选择“工具”下拉菜单，选择“数据分析”选项，然后单击“确定”。

第三步，在分析工具中选择“无重复双因素方差分析”，然后单击“确定”。当对话框出现时，在“输入区域”方框中输入数据单元区域A1:D4，在“α”输入0.05(可根据需要确定)。在“输出选项”中选择输出区域，单击“确定”后，得到如表8－18所示的输出结果。

表8－18　无重复双因素方差分析

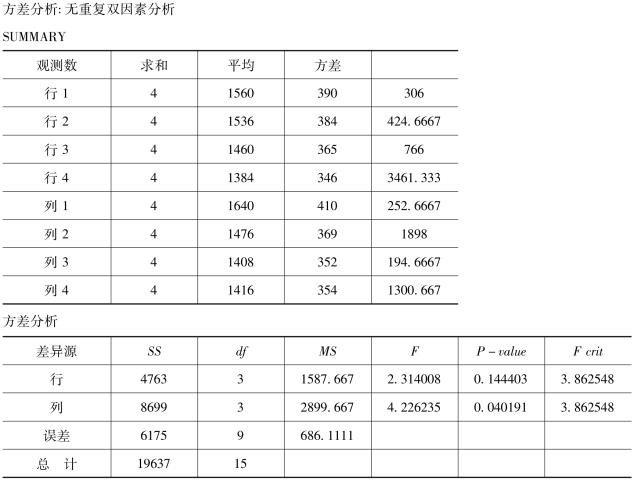
在表8－18中的“行”指行因素，即品牌因素;“列”指列因素，即地区因素。

三、利用Excel查χ2统计量的临界值

第一步，打开Excel，点击“插入”下拉菜单中的“fx函数(F)”，单击“统计”，在函数名菜单下选择“CHIINV”函数。

第二步，在出现对话框的“Probability“栏中键入0.01，在“Deg_freedom”栏中键入自由度4，单击“确定”得到临界值13.27670414。

思考与练习

一、判断题

1．方差分析是分析分类型自变量对数值型因变量的影响。(　)

2．方差分析中的每一个总体不一定都要服从正态分布。(　)

3．方差分析中的每一个总体的方差不一定要求相等。(　)

4．方差分析的统计决策规则是F＞Fα拒绝原假设。(　)

5．χ2检验可以进行独立性检验和拟合优度检验。(　)

二、单项选择题

1．方差分析中如果只涉及一个分类型自变量，称为(　)方差分析。

A．单因素　

B．多因素　

C．一元　

D．多元

2．方差分析实质上是一个(　)问题。

A．假设检验　

B．参数估计　

C．抽样推断　

D．样本容量确定

3．方差分析中所计算的统计量是(　)统计量。

A．t　

B．F　

C．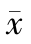　

D．σ

4．SSA的均方称为(　)。

A．组间方差　

B．组内方差　

C．总方差　D．组间平方和

5．列联分析中所计算的统计量是(　)。

A．t　

B．F　

C．珋　

D．χ2

三、多项选择题

1．单因素方差的步骤包括(　)。

A．提出假设　

B．构造检验统计量　

C．统计决策

D．计算总误差平方和　

E．计算组间误差平方和

2．方差分析的类型包括(　)。

A．提出假设　

B．构造检验统计量　

C．统计决策

D．单因素方差分析　

E．多因素方差分析

3．方差分析的假设包括(　)。

A．提出假设　

B．每个总体服从正态分布　

C．各总体方差相等

D．观测值是独立的　

E．显著性水平α= 0.05

4．若检验的统计量F近似等于1，说明(　)。

A．组间方差中不包含系统因素的影响

B．组内方差中不包含系统因素的影响

C．组间方差中包含系统因素的影响

D．方差分析中应拒绝原假设

E．方差分析中应接受原假设

5．对于单因素方差分析中的组内方差，下列哪种说法是正确的(　)。

A．其自由度为r－1　

B．反映的是随机因素的影响

C．反映的是随机因素和系统因素的影响　

D．其自由度为n－r

E．组内误差一定小于组间误差

四、简答题

1．什么是方差分析?方差分析的目的是什么?

2．方差分析的基本思想是什么?

3．单因素方差分析包括哪些步骤?

4．总方差与组间方差和组内方差的关系如何?

5．方差分析中，进行多重比较的原因如何?

五、计算题

1．从3个总体中各抽取样本量不同的样本数据，结果见下表，检验3个总体的均值之间是否有显著差异(α= 0.01)。

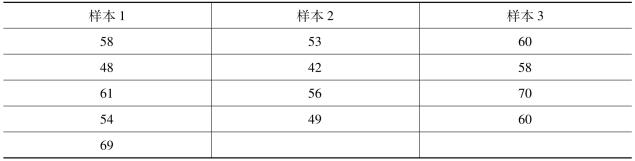
2．一家牛奶公司有4台机器装填牛奶，每桶的容量为4升。下表是从4台机器中抽取的样本数据。取显著水平α=0.01，检验4台机器的装填量是否相同。

3．某企业准备用4种方法组装一种新的产品，为确定哪种方法每小时生产的产品数量最多，随机抽取了32名工人，并制定每个人使用其中的一种方法，通过对每个工人生产的产品数量进行方差分析得到下面的结果:

(1)完成上面方差分析表;

(2)若显著性水平α= 0.05，检验4种方法组装的产品数量之间是否有显著差异。

4．一位英语老师在3个不同的小班采用不同的教学方法进行教学，一段时间之后，英语老师想知道3种不同的教学方法对学生的学习效果有无明显的影响，进行了一次测试，从各班中随机抽取一组样本，所得资料如下:

1班:73，89，82，43，80，73，66，60，45，93，36，77。

2班:88，78，48，91，51，85，74，56，77，31，78，62，76，96，80。

3班:68，79，56，91，71，71，87，41，59，68，53，79，15。

如果各班学生成绩服从正态分布，且方差相等，试在显著性水平α= 0.05下检验各班级的平均分数有无显著差异。

5．为检验广告媒体和广告方案对产品销售量的影响，一家营销公司做了一项试验，考察3种广告方案和两种广告媒体，获得的销售量数据如下表，检验广告方案、广告媒体对销售量的影响是否显著(α = 0.05)。

附表1　随机数字表

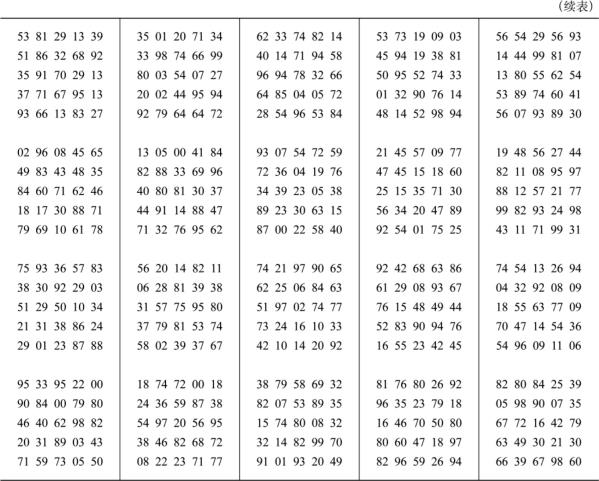
附表2　标准正态分布表

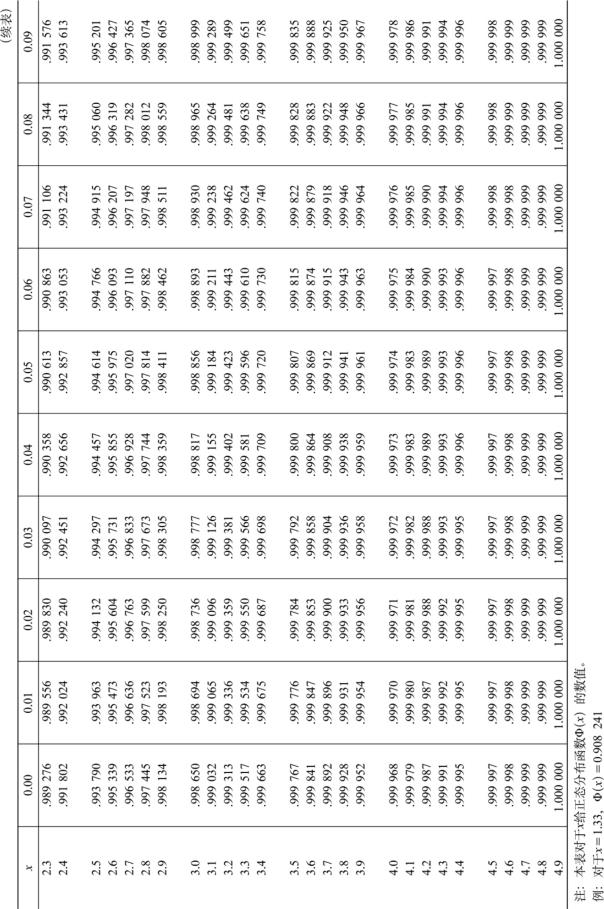
附表3　正态分布分为数表

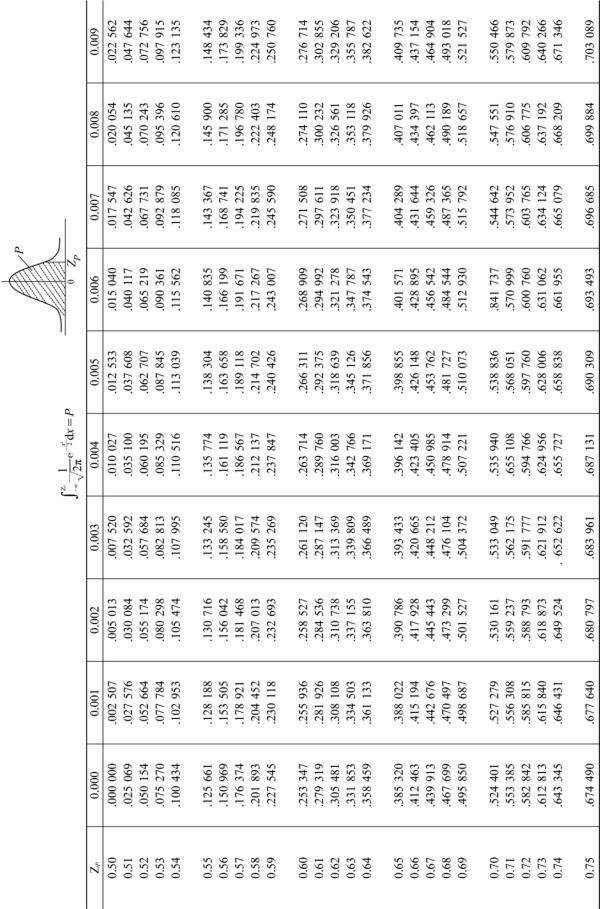
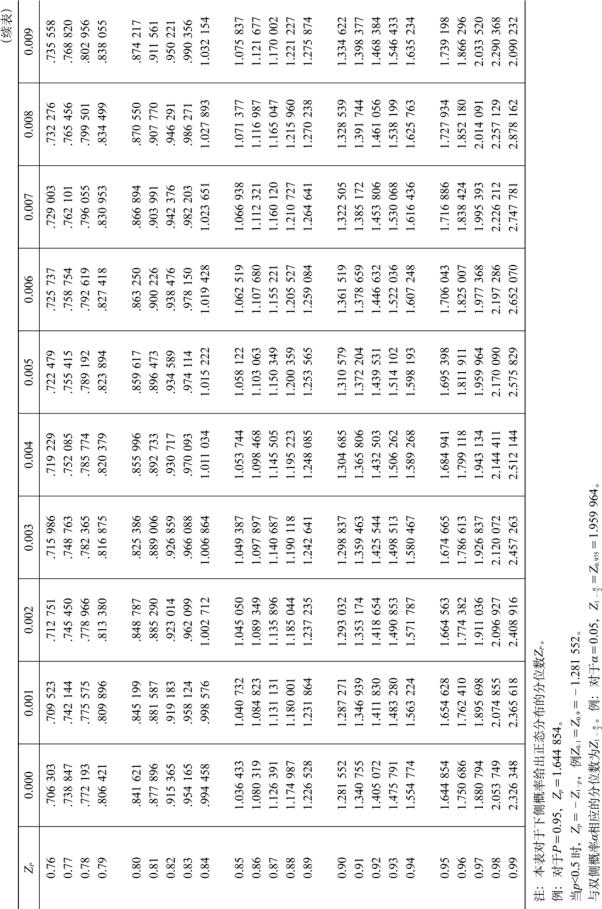
附表4　t 分布表

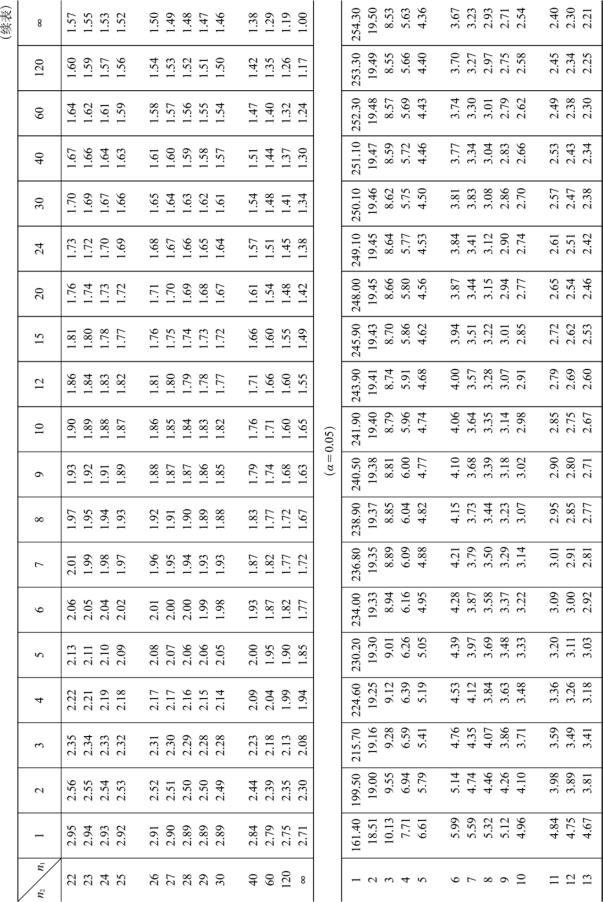
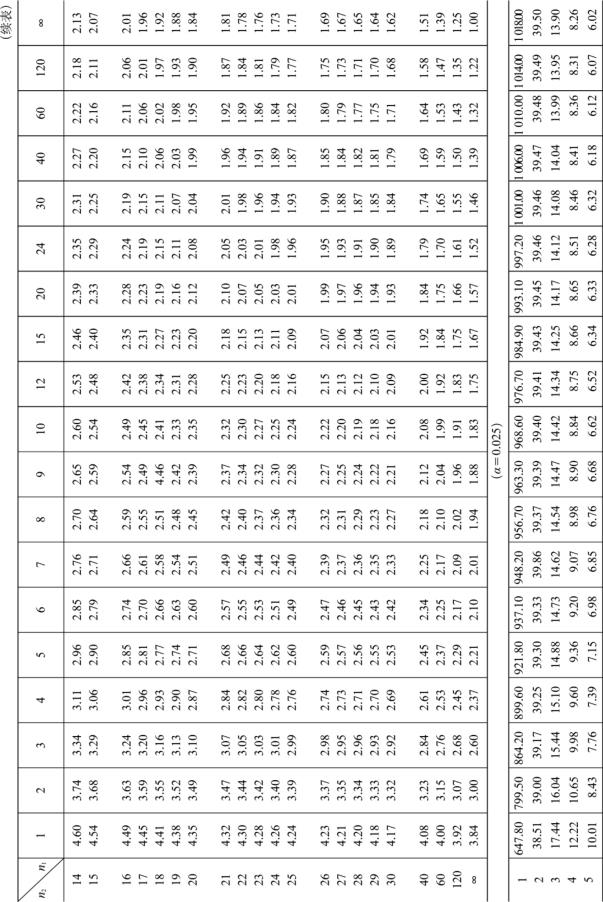
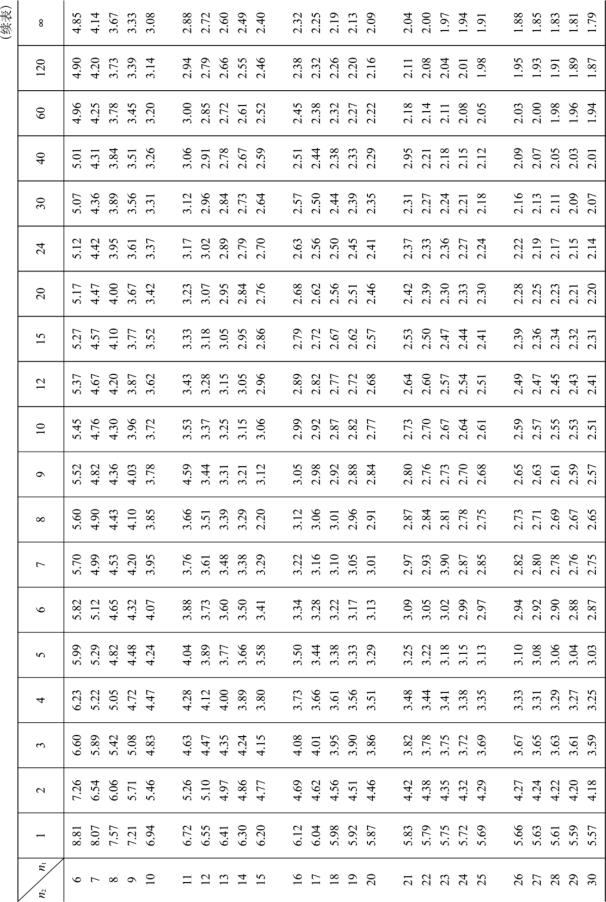
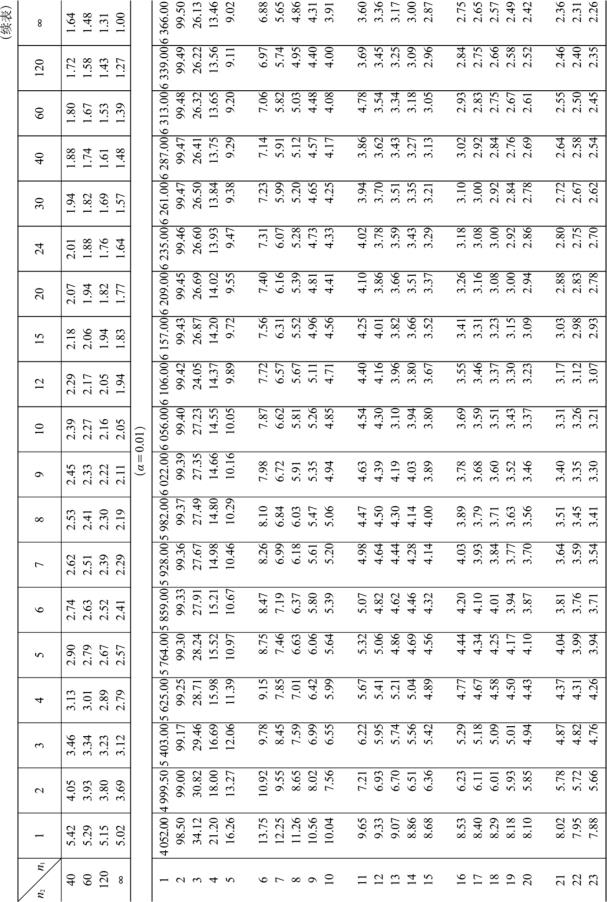
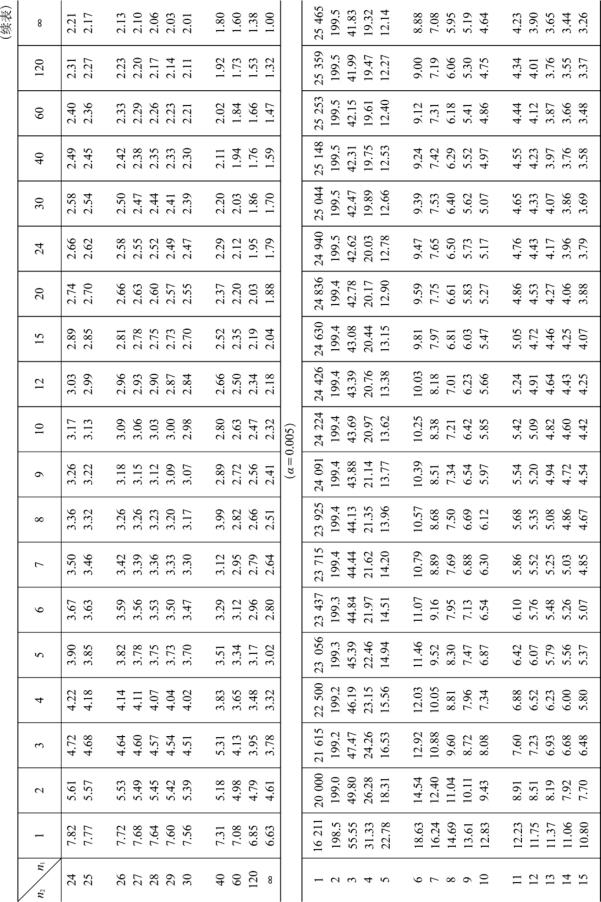
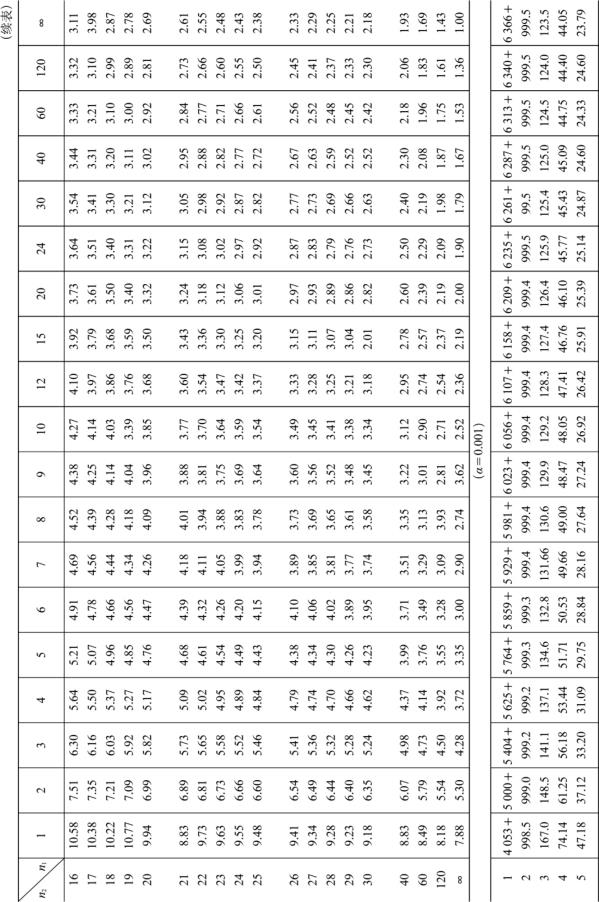
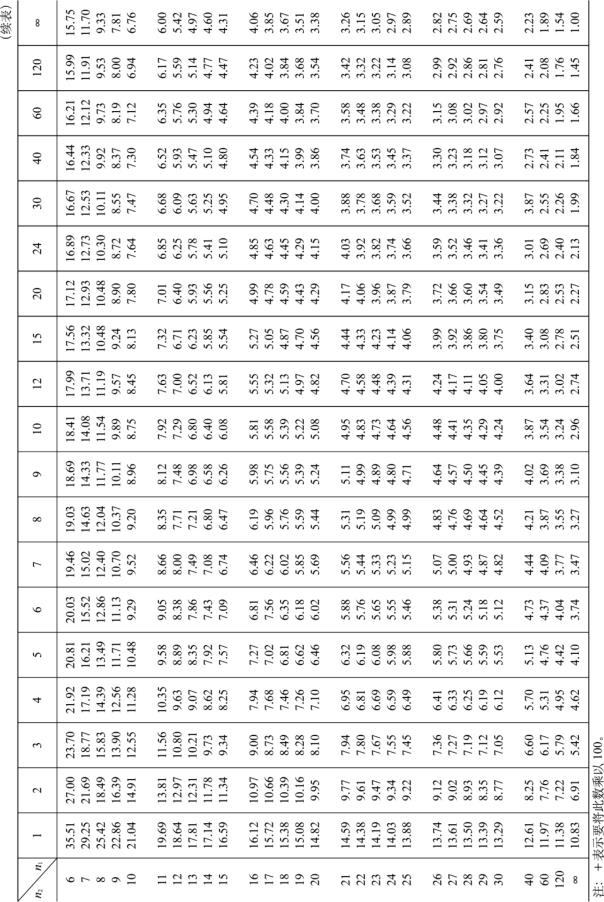
附表5　F 分布表