数据分布特征的描述和优化方法

第三章　数据分布特征的描述

通过调查获得、经过整理后展现的数据已经可以反映出被研究对象的一些特征，但认知程度还比较低，反映的精确度也不够。为此，我们还要使用另外一些特征值来准确地描述这些数据。对一组数据分布的特征，可以从3个方面进行测度和描述:集中趋势、离散趋势、偏态与峰度。

第一节　集中趋势的描述

集中趋势是指一组数据向某一中心值靠拢的倾向，它反映了一组数据中心点的位置所在。描述集中趋势也就是寻找数据一般水平的代表值或中心值。这一代表值或中心值在统计学中也称为平均值，平均值是同质总体内某一标志的各标志值的一般水平。本章所介绍的平均值包括测度分类数据集中趋势的众数，测度顺序数据集中趋势的中位数，测度数值性数据的算术平均数、调和平均数以及几何平均数。在前面我们把数据的类型分为分类型数据、顺序型数据、数值型数据，而且还指出，分类型数据是层次较低的数据，数值型数据是层次较高的数据，在统计学中，低层次数据的集中趋势的测度方法适用于高层次数据的测度，反过来，高层次数据的集中趋势的测度方法并不适用于低层次数据的测度。因此，选用哪一个测度值来反映数据的集中趋势，要根据所掌握的数据的类型和特点来确定。

一、分类型数据:众数(M o)

1．众数的概念

众数是指一组数据中出现次数最多的变量值，用Mo表示。从变量分布的角度看，众数是具有明显集中趋势点的数值，一组数据分布的最高峰点所对应的变量值即为众数。当然，如果数据的分布没有明显的集中趋势或最高峰点，众数也可能不存在;如果有多个高峰点，也就有多个众数。

众数是由变量值出现次数的多少决定的，不受资料中极端数值的影响，这样增强了众数对总体一般水平的代表性。

2．众数的计算方法

根据变量数列的不同种类，确定众数可采用不同的方法。

对于单项式变量数列确定众数的方法是观察次数，出现次数最多的变量值就是众数。

【例3－1】一种商品价格及销售量如表3－1所示，求众数。

表3－1　某种商品的价格及销售量情况

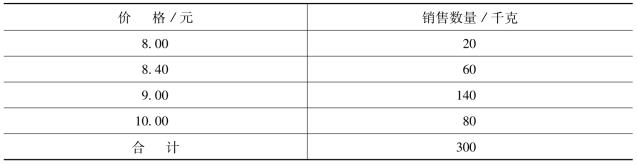
上表中价格为9.00元的商品销售量最多，即出现次数最多，则众数Mo= 9.00元。

对于组距式变量数列而言，确定众数时首先由次数的多少来确定众数所在组，次数最多的组就是众数组，然后再用比例插值法推算众数的近似值。其计算公式为:下限公式

上限公式

式中，XL，XU分别表示众数所在组的下限、上限;Δ1表示众数所在组次数与前一组次数之差; Δ2表示众数所在组次数与后一组次数之差;d表示众数所在组的组距。

由于各组次数可以用绝对数表示，亦可以用相对数表示，因此，根据次数来确定众数时，既可以根据绝对次数计算，也可以根据相对次数计算。下面以某班学生统计学的考试成绩为例(如表3－2所示)，计算众数。

表3－2　某班学生统计学的考试成绩情况表

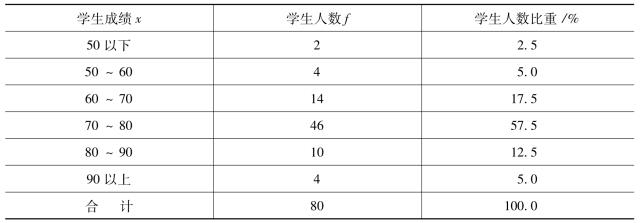
按绝对数计算，由下限公式:

按相对数计算，由上限公式:

二、顺序型数据:中位数(M e)

1．中位数的概念

中位数是将各单位标志值按大小排列，居于中间位置的那个标志值就是中位数，用Me表示。

2．中位数的计算

第一，由未分组数据确定中位数。对未分组数据，需先将各变量值按大小顺序排列，并按公式(m表示中位数的位置，n表示变量值的个数)确定中位数的位置。当一个序列中的项数为奇数时，则处于序列中间位置的变量值就是中位数。例如，根据7，6，8，2，3这5个数据求中位数，先按大小顺序排成2，3，6，7，8。在这个序列中，按来确定中位数的位置是，也就是序列中处于第三个位置的变量值就是中位数。本例中，中位数是6。

上例中，序列的项数为奇数，处于序列中间位置的只有一个变量值，这个值就是中位数。当一个序列的项数是偶数时，则应取中间两个数的中点值作为中位数，即取中间两个变量值的平均数为中位数。例如，一个按大小顺序排列的序列2，5，7，8，11，12，其中位数的位置在7与8之间，中位数就是7与8的平均数，即

第二，由单项式数列确定中位数。根据单项式数列资料确定中位数与根据未分组数据确定中位数的方法基本一致。它是先计算各组的累计次数(或频数)，仍然按上述公式确定中位数的位置，只不过这里的并对照累计次数确定中位数。

【例3－2】某班同学按年龄分组的资料如表3－3所示，求中位数。

表3－3　单项数列求中位数计算表

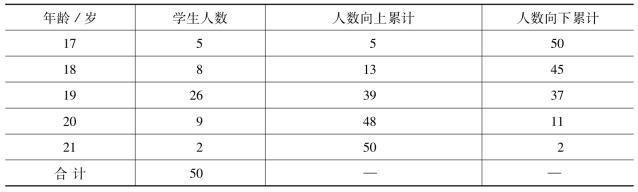
年龄中位数的位置为的含义是说明中位数位于第25个变量值和第26个变量值之间，本例中，无论是第25个数还是第26个数，根据累计次数可确定中位数均在第三组，为第三组的数值19岁。

第三，由组距数列确定中位数。如分组资料为组距式，应先按(这里的n=求出中位数所在组的位置，然后再用公式确定中位数的值。其计算公式为

下限公式(向上累计时用)

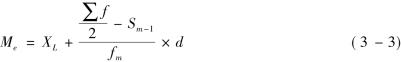
上限公式(向下累计时用)

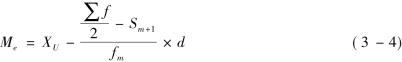
式中，XL、XU分别表示中位数所在组的下限、上限; fm中位数所在组的次数;Sm－1中位数所在组以前各组的累计次数;Sm+1中位数所在组以后各组的累计次数;∑f总次数;d中位数所在组的组距。

【例3－3】某班学生统计学期末考试成绩情况如表3－4所示，请计算其中位数。

表3－4　某班学生统计学期末考试成绩情况表

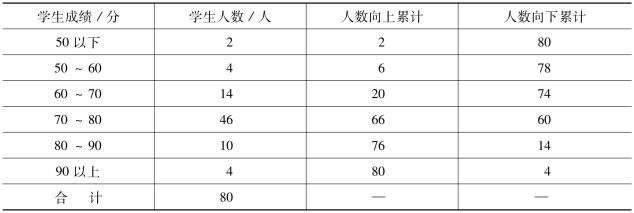
中位数位次，这里，40.5的含义是中位数位于第40个变量值和第41个变量值之间，从累计次数看，中位数在70～80这一组。

代入下限公式计算:

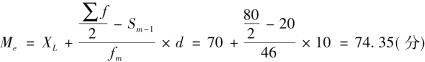
代入上限公式计算:

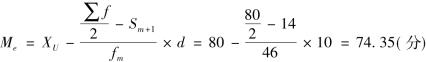
有必要强调指出，正如前述，众数和中位数都是均值。在经济实践中，如果我们只需要掌握某些现象的基本情况，则众数和中位数就可以满足这方面的需要，因为和其他类型的均值相比较，众数和中位数的计算过程简单，有的条件下，我们只需观察一下，就可以找出中位数和众数，而不需要繁琐的计算。

三、数值型数据:平均数

平均数在统计学中具有重要的地位，是集中趋势的最主要测度值，它主要适用于数值型数据，根据所掌握数据的不同，平均数有不同的计算形式和计算公式。

1．算术平均数

算术平均数是总体标志总量与总体单位总量的比值，一般用符号珋x表示。算术平均数是集中趋势中最主要的测度值。它的基本公式是:

由于所掌握的资料形式不同，算术平均数的计算分为简单算术平均数和加权算术平均数两种。

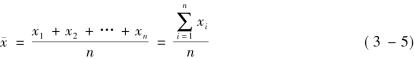
第一，简单算术平均数。根据未分组数据计算算术平均数。设一组数据为x1，x2，x3，…，xn，则【例3－4】5名学生的身高分别为1.65、1.69、1.70、1.71和1.75米，求他们的平均身高。

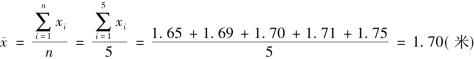
简单算术平均数之所以简单，就是因为各个变量值出现的次数均相同，例3－4中每个变量值出现的次数都是1。因此，只要把各项变量值简单相加再用项数去除就可求出平均数。

第二，加权算术平均数。根据分组数据计算平均数。设原始数据被分成n组，各组的变量值分别为x1，x2，x3，…，xn，各组变量值出现的次数分别为f1，f2，f3，…，fn，则

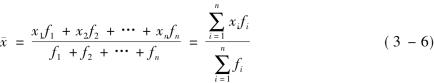
计算加权算术平均数运用的变量数列资料有两种:单项变量数列和组距变量数列。单项变量数列直接对各组变量值进行加权平均计算;组距变量数列需要先求出各组变量值的组中值，其作用是用它来代替各个组的平均数，然后，对组中值进行加权平均计算。

【例3－5】某车间50名工人加工某种零件的生产情况如表3－5所示，求人均日产量。

表3－5　某车间50名工人某种零件的生产情况

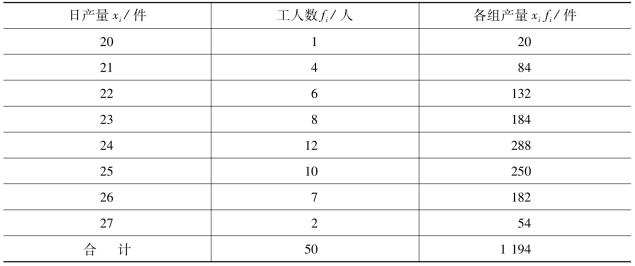
平均日产量为

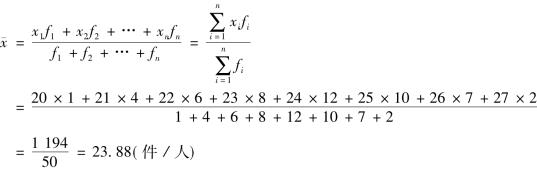
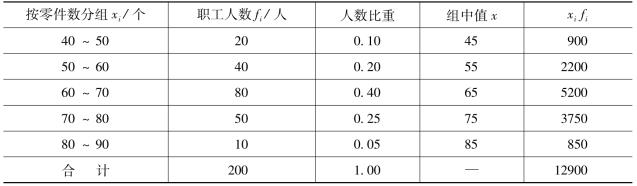
【例3－6】根据某车间200名工人加工零件的资料(表3－6)，计算平均每个工人的零件生产量。

表3－6　某车间职工加工零件平均数计算表

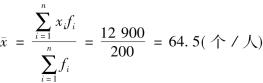
前面已经介绍过数值型变量，例3－5中的产量就是数值型变量，其取值20，21…就是变量值，每个变量值所对应的人数称为次数，也可以理解成每个变量值出现的次数，用f表示。从以上计算过程可以看出次数f的作用:当变量值比较大且次数多时，平均数就接近于变量值大的一方;当变量值比较小且次数多时，平均数就接近于变量值小的一方。可见，在计算平均数的过程中，次数对平均数的大小起着权衡轻重的作用，因此把次数也称为权数。把次数加入计算的平均数称为加权平均数。权数在经济实践中，尤其是在多指标的综合评价、统计指数以及统计预测中有着广泛的应用。

如果各组的次数(权数)均相同，求时，权数的权衡轻重作用也就消失了。这时，加权算术平均数与简单算术平均数计算结果相等，推导过程如下:可见，简单算术平均数实质上是加权算术平均数在权数相等条件下的一个特例。

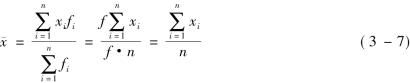
简单算术平均数的大小只与变量值的大小有关。加权算术平均数的大小不仅受各组变量值大小的影响，而且还受各组变量值出现的次数即权数大小的影响。

权数既可以用绝对数表示，也可以用相对数(比重)表示。因此，加权算术平均数也可用以下形式:

【例3－7】仍以表3－6的资料为例，当已知各组工人人数占全部工人人数的比重时，计算每个工人的平均产量。

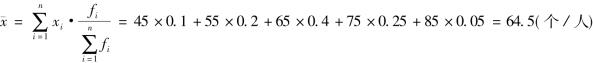
针对原始资料的不同形式，我们可以选择适合的公式形式，往往异曲同工。用比重(频率)公式计算出来的平均产量与原来用绝对数次数做权数计算的结果完全相同。这是因为权数的两种形式，其计算公式在本质上是一致的。

2．调和平均数

在统计分析中，有时会由于种种原因没有频数的资料，只有每组的变量值和相应的标志总量。在这种情况下就不能直接运用算术平均方法来计算了，而需要以迂回的形式，即用每组的标志总量除以该组的变量值推算出各组的次数，才能计算出平均数。这种方法就是调和平均数。

调和平均数是各变量值倒数的算术平均数的倒数。由于它是根据变量值倒数计算的，所以又称为倒数平均数，通常用表示。根据掌握的资料不同，调和平均数可分为简单调和平均数和加权调和平均数两种。

第一，简单调和平均数。根据未经分组资料计算平均数，我们先来看一个最简单的例子。

【例3－8】假如某种蔬菜在早、中、晚市每千克的单价分别为0.5元、0.4元、0.2元，若早、中、晚市各买1千克，其平均价格用简单算术平均数计算，结果是0.37元。但若早、中、晚市各买1元钱，其平均价格是多少?

计算方法应先把总购买量计算出来，然后再将总金额除以总购买量，即

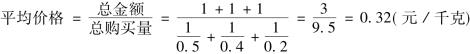
用公式表达即为:

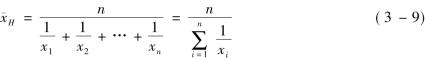
事实上简单调和平均数是权数相等条件下的加权调和平均数的特例。当权数不等时，就需要进行加权了。

第二，加权调和平均数。设m为加权调和平均数的权数，加权调和平均数公式为

【例3－9】仍用前面对蔬菜计算平均价格为例，如果现在早、中、晚市所花钱数不再是1元钱，而是如表3－7的情形，求购进的该种蔬菜的平均价格。

表3－7　调和平均数计算表

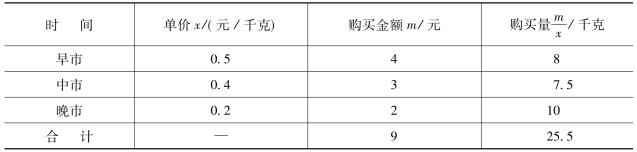
平均价格为

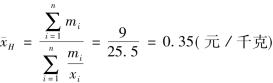
有必要指出的是，调和平均数是算术平均数的变形。在实际工作中，调和平均数通常是作为算术平均数的变形使用的，也就是由于受所掌握资料的限制，有时不能直接采用算术平均数的计算公式计算平均数，这就需要使用调和平均数的形式进行计算。

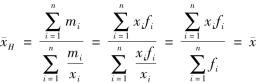
由此可见，调和平均数和算术平均数在本质上是一致的，唯一的区别是计算时使用了不同的数据。那么，如何判断在什么情况下可以采用算术平均数或调和平均数呢?关键在于以算术平均数的基本公式为依据进行判断。当我们“直接掌握”的是分母资料时，用算术平均数公式计算;当我们“直接掌握”的是分子资料时，用调和平均数公式计算。总之，由所掌握的资料条件来决定。例如，在已知每种价格x、销售量f时，用加权算术平均数求平均价格;在已知每种价格x、销售额m时，用加权调和平均数求平均价格。

3．几何平均数

几何平均数是n个变量值连乘积的n次方根。几何平均数是计算平均比率和平均速度最适用的一种方法，通常用表示。根据掌握的数据资料的不同，几何平均数可分为简单几何平均数和加权几何平均数两种。

第一，简单几何平均数。根据未经分组资料计算平均数。简单几何平均数的计算公式为:

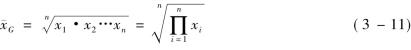
【例3－10】某产品生产需要经过六道工序，每道工序的合格率分别为98%，91%，93%，98%，98%，91%，求这六道工序的平均合格率。

因为成品的合格率等于各道工序产品合格率的连乘积，所以要用几何平均数来计算这六道工序的平均合格率，即

第二，加权几何平均数。当掌握的数据资料为分组资料，且各个变量值出现的次数不相同时，就要用加权方法计算几何平均数。加权几何平均数的计算公式为

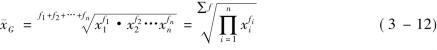
【例3－11】某市从2000年以来的14年，各年的工业增加值的增长率资料如表3－8所示，计算这14年的平均增长速度。

表3－8　几何平均数计算表

首先根据式(3－12)计算平均发展速度:

平均增长速度=平均发展速度－100%= 109.45%－100%= 9.45%四、众数、中位数和算术平均数的比较

算术平均数与众数、中位数的关系取决于频数分布的状况。它们的关系如下:

(1)当数据具有单一众数且频数分布对称时，算术平均数与众数、中位数三者完全相等，即

(2)当频数分布呈现右偏态时，则三者之间的关系为珋x＞Me＞Mo。

(3)当频数分布呈现左偏态时，则三者之间的关系为珋x＜Me＜Mo。

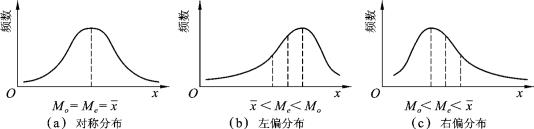
图3－1　众数、中位数和算术平均数的关系示意图

算术平均数与众数、中位数如果从数值上的关系看，当频数分布的偏斜程度不是很大时，无论是左偏还是右偏，众数与中位数的距离约为算术平均数与中位数的距离的两倍，即

第二节　离散趋势描述

集中趋势只是数据分布的一个特征，它所反映的是各变量值向其中心值聚集的程度。数据的分散程度是数据分布的另一个重要特征，它所反映的是各变量值远离其中心值的程度。集中趋势的各测度值是对数据一般水平的一个概括性度量，它对一组数据的代表程度取决于该组数据的离散水平。数据的离散程度越大，集中趋势的测度值对该组数据的代表性越差;离散程度越小，其代表性就越好。

描述数据离散程度的测度值主要有异众比率、极差、四分位差、平均差、方差和标准差、离散系数等，这些指标我们又称为变异指标。

一、变异指标的作用

(1)变异指标大小是平均数代表性的依据。变异指标变动愈大，平均数的代表性愈小;变异指标变动愈小，平均数的代表性愈大。

例如，某车间有两个生产小组，都是7名工人，各人日产量如下:

甲组:20，40，60，70，80，100，120

乙组:67，68，69，70，71，72，73

甲、乙两组的平均产量相等，即(件)。但甲组各工人日产量相差很大，分布很分散;而乙组各工人日产量相差不大，分布相对集中。因此，虽然平均数都是70件，但对甲组来说，其代表性要小得多;对乙组来说，其代表性相对较大。

(2)变异指标可用来反映社会生产和其他社会经济活动过程的均衡性或协调性，以及产品质量的稳定性程度。

例如，甲、乙两钢厂某年第一季度供货计划的完成情况如表3－9所示。

表3－9　甲、乙两钢厂某年第一季度供货计划完成程度统计表

从表3－9的资料来看，两厂供货计划虽然都已完成，但计划执行的均衡性不同，甲厂按月均衡地完成了规定的季度供货计划，而乙厂前松后紧，1，2月份总共完成计划的50%，3月份再完成计划的50%，这样就缺乏均衡性。

又如，对一批产品的质量指标，如灯泡的耐用时间、轮胎的行驶里程等，测定其标志变动度，如果变异指标值大，则说明产品质量不稳定;如果变异指标值小，则产品质量显得稳定。

二、分类型数据离散趋势的测定

分类数据离散程度的测定用异众比率这一指标。异众比率是指非众数组的频数占总频数的比率，主要用于测度分类型数据的离散程度，计算公式为

式中，vr表示异众比率;

表示变量值的总频数; fm表示众数组的频数。

异众比率的作用是衡量众数对一组数据的代表程度。异众比率越大，说明非众数组的频数占总频数的比重越大，众数的代表性就越差;异众比率越小，说明非众数组的频数占总频数的比重越小，众数的代表性越好。

【例3－12】根据例3－1的数据计算价格为9.00元的商品的异众比率。

根据公式(3－15)，得

这里53.3%的含义是用9.00元作为这种商品的平均价格，其代表程度是53.3%。

三、顺序型数据离散趋势的测定

(一)四分位数

中位数是从中间点将全部数据等分为两部分。与中位数类似的还有四分位数、八分位数、十分位数和百分位数等。它们分别是用3个点、7个点、9个点和99个点将数据四等分、八等分、十等分和一百等分后各分位点上的值。这里只介绍四分位数的计算，其他分位数与之类似。

1．四分位数

一组数据排序后处于25%和75%位置上的值，称为四分位数，也称四分位点。

四分位数是通过3个点将全部数据等分为四部分，其中每一部分包含25%的数据。很显然，中间的分位数就是中位数，因此通常所说的四分位数是指处在25%位置上的数值(下四分位数)和处在75%位置上的数值(上四分位数)。与中位数的计算方法类似，根据未分组数据计算四分位数时，首先对数据进行排序，然后确定四分位数所在的位置。

2．四分位数的确定

设下四分位数为QL，上四分位数为QU。

(1)未分组数据

当四分位数的位置不在某一个位置上时，可根据四分位数的位置，按比例加权计算四分位数。

(2)单变量值分组数据

(3)组距分组数据

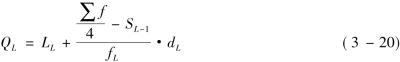
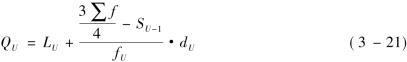
式中，LL，LU分别表示QL，QU所在组的下限; fL，fU分别表示中位数所在组的次数;SL－1，SU－1分

别表示QL，QU所在组的以后各组的累计次数(向上累计); 表示总次数;dL、dU分别表示QL，QU所在组的组距。

(二)四分位差

四分位数是离散程度的测度值之一，是上四分位数与下四分位数之差，又称为四分位差，亦称为内距或四分间距，用Qd表示。四分位差的计算公式为

四分位差反映了中间50%数据的离散程度，其数值越小，说明中间的数据越集中;数值越大，说明中间的数据越分散。四分位差主要用于测度顺序型数据的离散程度。它克服了极差容易受极端值的影响这一缺陷。此外，由于中位数处于数据的中间位置，因此，四分位差的大小在一定程度上也说明了中位数对一组数据的代表程度。四分位差主要用于测度顺序数据的离散程度，当然对于数值型数据也可以计算四分位差，但不适合于分类数据。四、数值型数据离散趋势的测定

1．极差

极差也称全距，它是一组数据中极大值与极小值之差，用R表示。如果根据未分组资料或者单项式变量数列计算极差，则

如果根据组距式变量数列计算极差，则

极差是描述数据离散程度的最简单测度值，计算简单，易于理解，但它容易受极端值的影响。由于极差只是利用了一组数据两端的信息，不能反映出中间数据的分散状况，因而不能准确描述出数据的分散程度。

【例3－13】学生外语考试中，最低分为48分，最高分为96分。

2．平均差

平均差也称为平均离差，是各变量值与其平均数离差绝对值的平均数，通常用MD表示。由于各变量值与其平均数离差之和等于零，所以，在计算平均差时要取绝对值。平均差的计算根据掌握数据资料的不同分为简单式平均差和加权式平均差。

(1)简单式平均差。对未经分组的数据资料，采用简单式，以例3－14来说明。

【例3－14】计算5，11，7，8，9的平均差。

平均差的计算过程分为四步:①计算数列的算术平均数，本例为8。②计算离差，其计算方法是用每个变量值与算术平均数相减，即:离差= xi－珋x。③计算离差的绝对值，因为均值处于一组数据的中心，所以离差有正有负，所有离差的代数和为0，无法进一步计算，取每个离差的绝对值，就可以做进一步的计算了。④计算离差绝对值的均值，即平均差，也就是如下的计算过程:

把上述计算过程用符号表示为

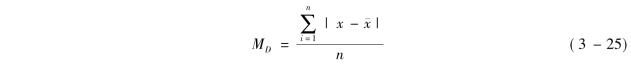
(2)加权式平均差。根据分组数据计算平均差，应采用加权式，其计算过程与简单式平均差的计算过程相同，仍然分为四步，只不过在计算离差绝对值均值时要用加权式，公式为

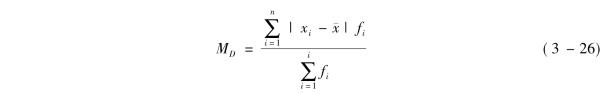
【例3－15】利用表3－10的资料计算平均差。

表3－10　平均差计算示例表

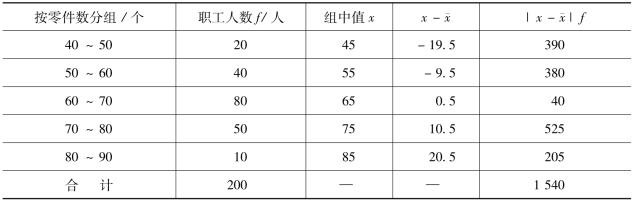
将表3－10的资料代入公式中，计算得

一组数据平均差的数值越大，则其平均数的代表性越小，说明该组变量值分布越分散;反之，平均差的数值越小，则其平均数的代表性越大，说明该组变量值分布越集中。

平均差由于采用绝对值的离差形式加以数学假定，在应用上有较大的局限性。

3．标准差

标准差又称为均方差，它是各单位变量值与其平均数离差平方的平均数的方根，通常用σ表示。标准差的平方称为方差，用σ2表示。标准差是测度数据离散程度的最主要方法。标准差是具有量纲的，它与变量值的计量单位相同。

根据掌握的数据资料的不同，有简单式和加权式两种。

(1)简单式。对未经分组的数据资料，采用简单式。

标准差的计算分为五步:①计算数列的算术平均数。②计算离差，其计算方法是用每个变量值与算术平均数相减，即:离差= xi－珋x。③计算离差的平方，即:离差平方=(xi－珋x)2，计算离差平方的原因是为了统一各个离差的符号，以便做进一步的计算。④计算离差平方的均值，即方差，即

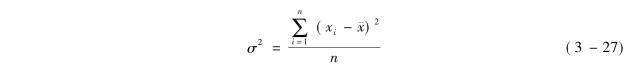
方差也是统计学中一个十分重要的概念，在经济实践以及统计分析中有着广泛的应用。但方差有两个缺陷，一个缺陷是为了统一符号给离差取平方，这就使得方差的数值要比现象实际的变异程度大很多倍，也就是说把现象的变异程度夸大了;另一个缺陷是方差没有量纲，如果有量纲要带一个平方，不易理解，为了克服这两个缺陷，取方差的方根。⑤取方差的方根，就是标准差，即

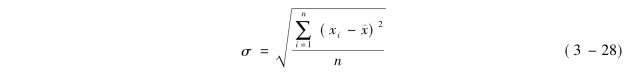
【例3－16】计算5，11，7，8，9的标准差。

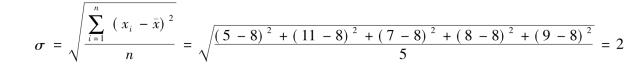
(2)加权式。根据分组整理的数据计算标准差，应采用加权式，其计算过程前已述及，只不过在这里计算离差平方的均值时，要把权数加入计算，公式如下:

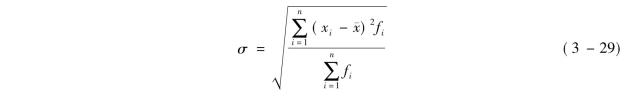
【例3－17】利用表3－11的资料计算标准差。

表3－11　标准差计算示例表

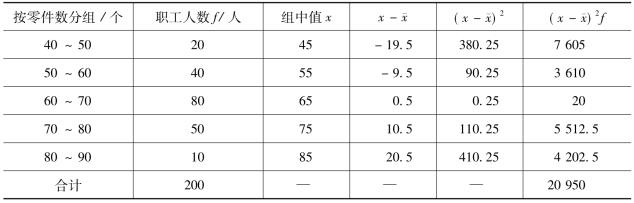
将表3－11的资料代入公式，计算得

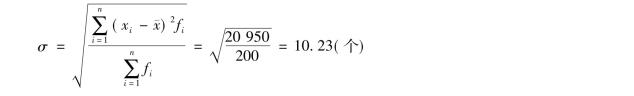
与平均差相比，标准差在数学处理上是通过平方消除离差的正负号，更便于数学上的处理。因此，标准差是实际中应用最广泛的离散程度测度指标。

标准差有总体标准差与样本标准差之分，上面我们介绍的是总体标准差，如果要计算样本标准差，只需在分母上减1即可。一般我们把样本标准差记为s，所以对简单式而言，有

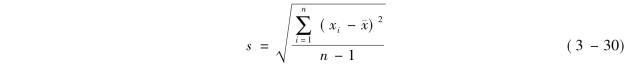
对加权式而言，有

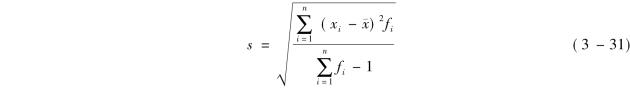
用σ2表示总体的方差，用s2表示样本的方差，在今后的统计分析中这些指标我们经常要用到。

4．离散系数

上面介绍的平均差、方差和标准差等都是反映数据分散程度的绝对值，其数值的大小一方面取决于原变量值本身水平高低的影响，也与变量的均值大小有关。变量值绝对水平高的，离散程度的测度值自然也就大;绝对水平低的，离散程度的测度值自然也就小。另一方面，它们与原变量值的计量单位相同，采用不同计量单位计量的变量值，其离散程度的测度值也就不同。因此，对于平均水平不同或计量单位不同的数列而言，为消除变量值水平高低和计量单位不同对离散程度测度值的影响，需要计算离散系数。

离散系数，是一组数据的标准差与其相应的均值之比，是测度数据离散程度的相对指标。离散系数通常是就标准差来计算的，因此也称为标准差系数。其计算公式为

离散系数的作用主要是用于比较不同总体或样本数据的离散程度。离散系数大的说明数据的离散程度也就大，离散系数小的说明数据的离散程度也就小。

【例3－18】某地两个不同类型的企业全年平均月产量资料如表3－12所示，计算离散系数。

表3－12　离散系数比较分析表

炼钢厂的标准差比纺纱厂大，但我们却不能直接断定炼钢厂的平均月产量的代表性就比纺纱厂的小。因为，首先这两个厂的平均月产量相差悬殊，其次两个厂属于性质不同(计量单位不同)的两个企业。因此只能根据离散系数的大小来判断。表3－12中最后一栏的两个企业的离散系数表明，炼钢厂的平均月产量的代表性就比纺纱厂的大，生产比较稳定。其结果与用标准差判断的结果正好相反。

第三节　数据分布偏态与峰度的测定

集中趋势和离散趋势是数据分布的两个重要特征，但要全面了解数据分布的特点，还需要知道数据分布的形状是否对称、偏斜的程度以及分布的扁平程度等。偏态和峰度就是对这些分布特征的描述。偏态是对数据分布在偏移方向和程度所做的进一步描述;峰度是用来对数据分布的扁平程度所做的描述。对于偏斜程度的描述用偏态系数，扁平程度的描述用峰度系数。

一、动差

动差又称为矩，原是物理学上用以表示力与力臂对重心关系的术语，这个关系和统计学中变量与权数对平均数的关系在性质上很类似，所以统计学也借用动差来说明频数分布的性质。

一般地说，取变量的a值为中点，所有变量值与a之差的K次方的平均数称为变量x关于a的K阶动差。用式子表示为

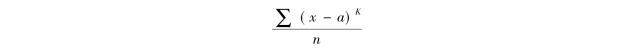
当a= 0时，即变量以原点为中心，上式称为K阶原点动差，用大写英文字母M表示。

一阶原点动差:

二阶原点动差:

三阶原点动差:

当a=珋x时，即变量以算术平均数为中心，上式称为K阶中心动差，用小写英文字母m表示。

一阶中心动差: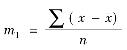

二阶中心动差:

三阶中心动差:

二、偏态及其测度

偏态是对分布偏斜方向及程度的度量。从前面的内容中我们已经知道，频数分布有对称的，有不对称即偏态的。在偏态的分布中，又有两种不同的形态，即左偏和右偏。虽然我们可以利用众数、中位数和算术平均数之间的关系判断分布是左偏还是右偏，但要度量分布偏斜的程度，就需要计算偏态系数了。

采用动差计算偏态系数是用变量的三阶中心动差m3与σ3进行对比，计算公式为

(www.xing528.com)

当分布对称时，变量的三阶中心动差m3由于离差三次方后正负相互抵消而取得0值，则α= 0;当分布不对称时，正负离差不能抵消，就形成正的或负的三阶中心动差m3。当m3为正值时，表示正偏离差值比负偏离差值要大，可以判断为正偏或右偏;反之，当m3为负值时，表示负偏离差值比正偏离差值要大，可以判断为负偏或左偏。|m3|越大，表示偏斜的程度就越大。由于三阶中心动差m3含有计量单位，为消除计量单位的影响，就用σ3去除m3，使其转化为相对数。同样的，α的绝对值越大，表示偏斜的程度就越大。偏态系数α的数值一般在0与±3之间，α越接近0，分布的偏斜度越小;α越接近±3，分布的偏斜度越大。

【例3－19】某管理局所属30个企业2013年3月份利润额统计资料如表3－13所示，要求计算该变量数列的偏斜状况。

表3－13　偏斜系数计算示例表

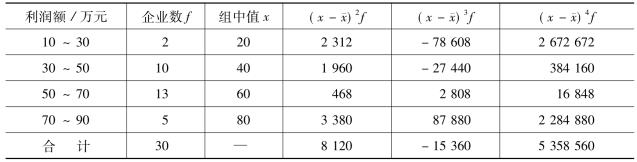
利用表3－13中有关数据计算标准差如下:

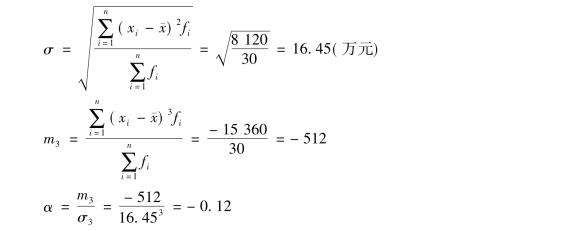
计算结果表明，该管理局所属企业利润额的分布状况呈轻微负偏分布。

三、峰度及其测度

峰度是用来衡量分布的集中程度或分布曲线的尖峭程度的指标，其计算公式为

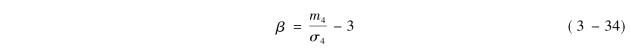
当峰度β＞0时，表示分布的形状比正态分布更瘦更高，这意味着分布比正态分布更集中在平均数周围，这样的分布称为尖峰分布，如图3－2(a)所示;β= 0时，分布为正态分布;β＜0，表示分布比正态分布更扁平，意味着分布比正态分布更分散，这样的分布称为扁平分布，如图3－2(b)所示。

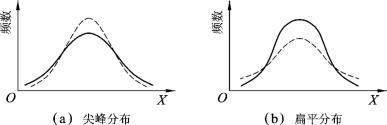
图3－2　尖峰分布与扁平分布示意图

【例3－20】继续例3－19，要求计算该变量数列的峰度。

根据表3－13中有关数据，计算峰度系数如下:

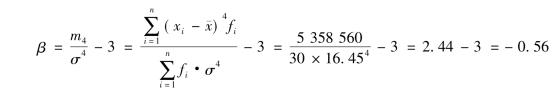
计算结果表明，上述企业间利润额的分布呈平顶峰度，各变量值分布较为均匀。

第四节　运用Excel进行描述统计

Excel中用于计算描述统计量的方法有两种，即函数方法和描述统计工具的方法。

一、用函数计算描述统计量

常用的描述统计量有众数、中位数、四分位数、算术平均数、几何平均数、极差、内距(四分位差)、标准差、方差、离散系数、偏态系数、峰度系数等。一般来说，在Excel中求这些统计量，未分组资料可用函数计算，已分组资料可用公式计算。

1．未分组资料用函数计算

【例3－20】我们把某电脑公司2013年前4个月每天的销售量输入到图3－3的A1单元格到A120单元格(这里只展示部分资料，单位:台)。

Excel中提供了插入统计函数的功能，如图3－4所示。也可以自己输入函数，如图3－5所示。

用函数方法求统计量，应先将120个原始数据输入A1∶A120单元格，然后单击任一空单元格，输入相应公式，回车后即可得计算结果。

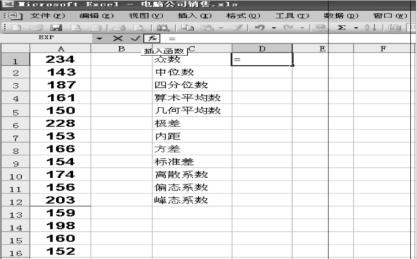
图3－3　电脑销售数据图

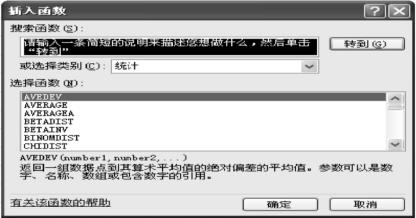
图3－4　插入函数对话框

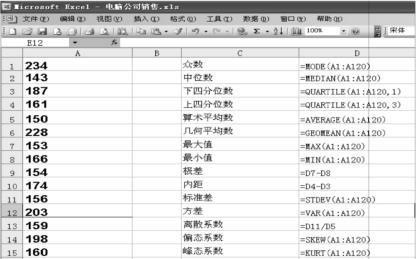
图3－5　手动输入函数图

计算结果如图3－6所示。

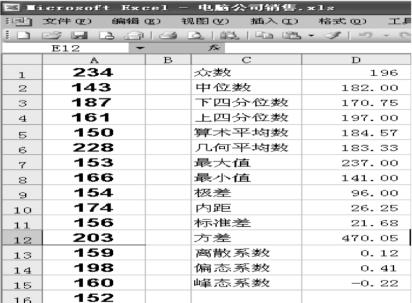
图3－6　输出结果图

2．已分组资料用Excel及公式计算

此处以标准差举例加以说明。

【例3－21】某企业工人日产量情况如表3－14所示，求标准差。

表3－14　某企业工人日产量的加权标准差计算表

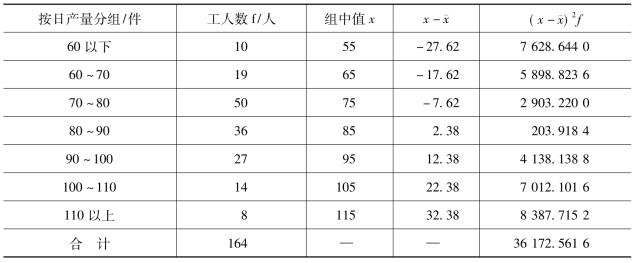
用Excel进行加权平均式标准差的计算:

1)先求出每名工人平均日产零件数82.62。

2)中文输入法选择单元格D2，在其中输入“=C2－82.62”，回车得第一组离差。

3)依次选择单元格D3至D8，重复步骤2);或把光标移至D2单元格右下角，当光标变为黑十字星时，按住鼠标右键并拖到D8区域松开，得各组离差。

4)选择单元格E2，输入“=D2* D2* B2”，回车后得加权绝对离差平方。

5)依次选择单元格E3至E8，重复步骤4);或把光标移至E2单元格右下角，当光标变为黑十字星时，按住鼠标右键并拖到E8区域松开，得各组加权绝对离差平方。

6)选择单元格E2至E8区域，单击自动求和图标“∑”按钮，得各加权绝对值离差平方的总和36 172.561 6。

7)在单元格A11中输入“标准差=”字样;选择单元格E11，在其中输入“= E9/B9”，回车得加权式标准差，如图3－7所示。

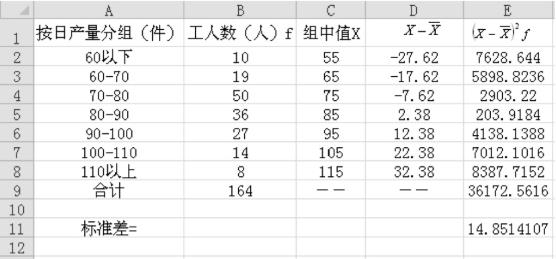
图3－7　加权式标准差的计算

二、描述性统计

用Excel计算平均数、标准差等描述性统计量有两种方法，一是用函数，二是用“数据分析”工具。这里只介绍后者。

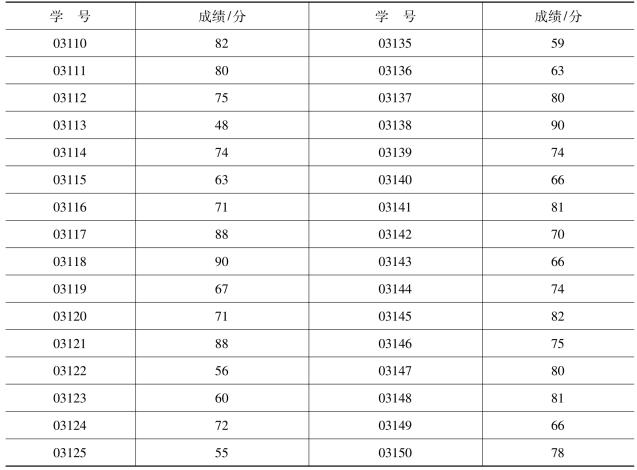
【例3－22】某班50名学生的英语成绩如表3－15所示，试计算描述统计量。

表3－15　某班学生英语成绩表

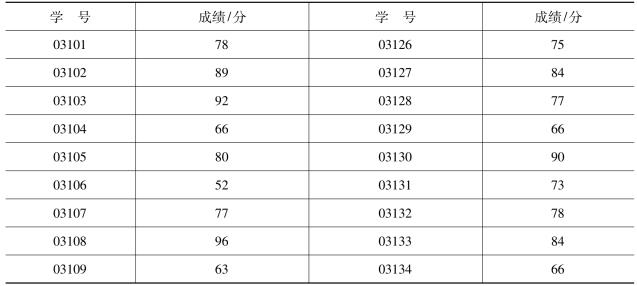
(续表)

操作步骤如下:

1)将学生学号输入A2到A51单元格，将学生成绩输入B2到B51单元格。

2)打开“工具”菜单，选择“数据分析”选项，打开“数据分析”对话框，选择“描述统计”分析工具，如图3－8所示。

图3－8　数据分析对话框

3)单击“确定”按钮，打开“描述统计”对话框。在输入区域中输入:$B$2∶$B$51，分组方式选择“逐列”，选中“标志位于第一行”复选框，若分组方式为“逐行”，则为“标志位于第一列”。如果输入区域没有标志项，该复选框被清除。在输出区域中任选一单元格(为输出结果左上角单元格地址，如$G$7)，单击“汇总统计”，如不选此项，则Excel省略部分输出结果，如图3－9所示。

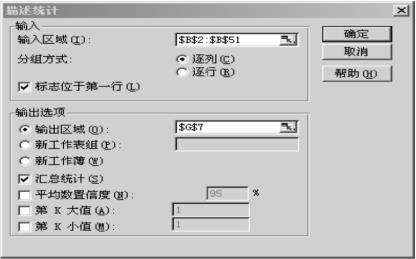
图3－9　描述统计对话框

4)单击“确定”按钮，将产生输出结果，如图3－10所示。

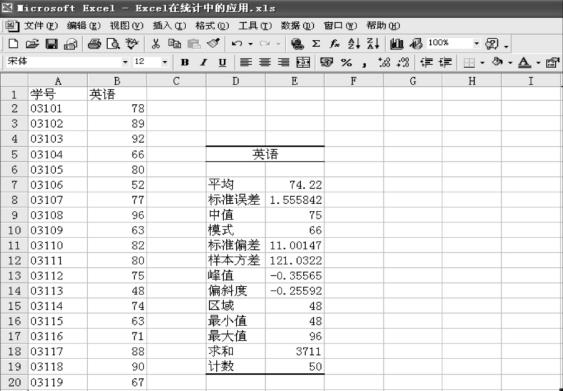
图3－10　描述统计输出结果

在输出结果中:

平均——算术平均数

标准误差——估计标准误差

中值——中位数

模式——众数

标准偏差——样本标准差s

样本方差——s平方

峰值——反映钟形分布峰高的一个指标

偏斜度——反映偏斜程度的一个指标

区域——全距，等于最大值减最小值

计数——单位数

从图3－10的结果可以看出，采用分析工具中的描述统计功能，不必利用统计函数或者公式去求解一个个的统计量，而能直接将平均数、标准差、众数、中位数、最大值、最小值等一次全部给出，能大大提高统计效率。

【思考与练习】

一、判断题

1．总体中各标志值之间的差异程度越大，标准差就越小。(　)

2．平均指标只受变量值大小的影响。(　)

3．平均指标反映总体的离散趋势，变异指标反映总体的集中趋势。(　)

4．偏态系数与峰度系数的取值范围都是－3与+ 3之间。(　)

5．变量数列的分布呈右偏分布时，算术平均数的值最小。(　)

6．中位数和众数都属于平均数，因此它们数值的大小受到总体内各单位标志值大小的影响。(　)

7．在特定条件下，加权算术平均数可以等于简单算术平均数。(　)

8．众数是总体中出现次数最多的值。(　)

9．数据分布的形状主要是指它分布的偏斜程度和峰的扁平程度。(　)

10．离散系数可以说明平均数的代表性大小。(　)

二、单项选择题

1．平均数反映了(　)。

A．总体分布的集中趋势　

B．总体中总体单位分布的集中趋势

C．总体分布的离散趋势　

D．总体变动的趋势

2．加权算术平均数的大小(　)。

A．受各组次数f的影响最大　

B．受各组标志值x的影响最大

C．只受各组标志值x的影响　

D．受各组次数f和各组标志值x的共同影响

3．已知某局所属12个工业企业的职工人数和工资总额，要求计算该局职工的平均工资，应该采用

(　)。

A．简单算术平均法　

B．加权算术平均法

C．加权调和平均法　

D．几何平均法

4．在某城市随机抽取13个家庭，调查得到每个家庭的人均月收入数据如下:1 080、750、1 080、850、960、2 000、1 250、1 080、760、1 080、950、1 080、660，则其众数和中位数分别为(　)。

A．1 080，1 600　

B．1 080，1 080　

C．950，1 250　

D．750，1 080

5．在下列两两组合的平均指标中，哪一组的两个平均数不受极端值的影响?(　)

A．算术平均数和调和平均数　

B．几何平均数和众数

C．调和平均数和众数　

D．众数和中位数

6．当一组数据属于左偏分布时，则(　)。

A．平均数、中位数与众数是合而为一的　

B．众数在左边、平均数在右边

C．众数的数值较小，平均数的数值较大　

D．众数在右边、平均数在左边

7．2007年某地区甲、乙两类职工的月平均收入分别为1 060元和3 350元，标准差分别为230元和680元，则职工平均收入的代表性(　)。

A．甲类较大　

B．乙类较大

C．两类相同　

D．在两类之间缺乏可比性

8．对于对称分布的数据，众数、中位数和平均数的关系是(　)。

A．众数＞中位数＞平均数　

B．众数=中位数=平均数

C．平均数＞中位数＞众数　

D．中位数＞众数＞平均数

9．如果某个分布是极度右偏，则其偏度系数为(　)。

A．－0.3　

B．0.3　

C．－2.9　

D．2.9

10．离散程度的测度值愈大，则(　)。

A．反映变量值愈分散，算术平均数代表性愈差

B．反映变量值愈集中，算术平均数代表性愈差

C．反映变量值愈分散，算术平均数代表性愈好

D．反映变量值愈集中，算术平均数代表性愈好

三、多项选择题

1．如果某个分布是左偏，并且是尖峰，则(　)。

A．α=－2　

B．β=－2　

C．α=2　

D．α= 0　

E．β= 2

2．不同数据组间各标志值的差异程度可以通过标准差系数进行比较，因为标准差系数(　)。

A．消除了不同数据组各标志值的计量单位的影响

B．消除了不同数列平均水平高低的影响

C．消除了各标志值差异的影响

D．数值的大小与数列的差异水平无关

E．数值的大小与数列的平均数大小无关

3．数据的分布特征可以从哪几个方面测度和描述(　)。

A．集中趋势　

B．分布的偏态　

C．分布的峰态　

D．离散程度　

E．长期趋势

4．受极端变量值影响的集中趋势度量指标是(　)。

A．众数　

B．中位数　

C．算术平均数　

D．调和平均数　

E．几何平均数

5．众数是(　)。

A．总体一般水平的代表值

B．总体中出现次数最多的标志值

C．不受极端值的影响

D．适用于总体单位数多，有明显集中趋势的情况

E．处于变量数列中点位置的那个标志值

6．中位数是(　)。

A．由标志值在变量数列中所处的位置决定的

B．根据标志值出现的次数决定的

C．总体单位水平的平均值

D．总体一般水平的代表值

E．不受总体中极端数值的影响

7．关于极差，下列说法正确的有(　)。

A．只能说明变量值变异的范围

B．不反映所有变量值差异的大小

C．反映数据的分配状况

D．最大的缺点是受极端值的影响

E．最大的优点是不受极端值的影响

8．在什么条件下，加权算术平均数等于简单算术平均数(　)。

A．各组次数相等　

B．各组标志值不等

C．变量数列为组距变量数列　

D．各组次数都为1

E．各组次数占总次数的比重相等

9．加权算术平均数的计算公式有(　)。

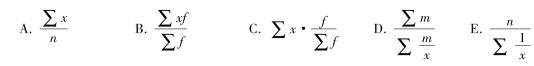
10．比较两组的工作成绩:算术平均数甲组小于乙组，标准差甲组大于乙组，则(　)。

A．乙组算术平均数代表性高于甲组　

B．甲组算术平均数代表性高于乙组

C．乙组工作的均衡性好于甲组　

D．甲组工作的均衡性好于乙组

E．甲组离散程度大于乙组

四、简答题

1．一组数据的分布特征可以从哪几个方面进行测度?

2．什么是简单算术平均数和加权算术平均数?分别写出计算公式。

3．什么是权数?权数对算术平均数有什么影响?

4．在什么条件下适用几何平均法来计算平均指标?

5．写出众数和中位数、算术平均数之间的关系。

6．简述众数、中位数和均值的特点与应用场合。

7．平均数的计算方法通常有几种?

8．简述变异指标的概念和作用。

9．为什么要计算离散系数?

10．测度数据分布形状的指标有哪些?

五、计算题

1．企业60名工人包装某产品的数量资料如表所示:

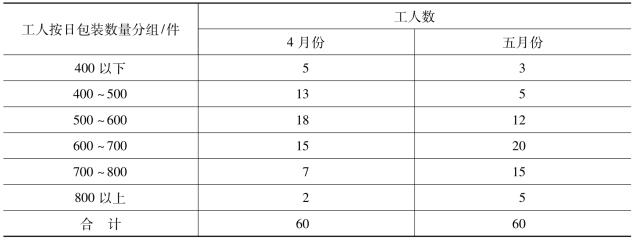
试计算4、5月份的劳动生产率，并指出4、5月劳动生产率高低不等的原因。

2．某市场有3种不同的苹果，其单价分别为2元/kg，3元/kg和4元/kg。

试计算:

(1)各买1kg，平均每千克多少钱?

(2)各买1元，平均每千克多少钱?

3．某高校某系学生的体重资料如表所示:

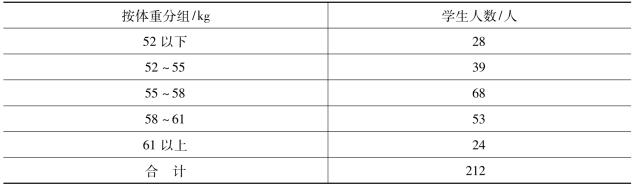
试根据所给资料用算术平均数和众数计算学生的平均体重。

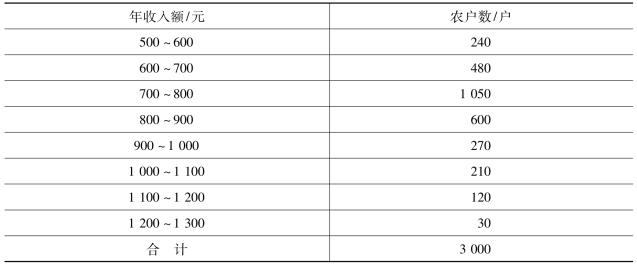
4．某乡镇农户年收入额的分组资料如下表所示，试确定其中位数及众数。

5．有甲、乙两个生产小组，甲组平均每个工人的日产量为36件，标准差为9.6件，乙组工人日产量资料如下表所示。

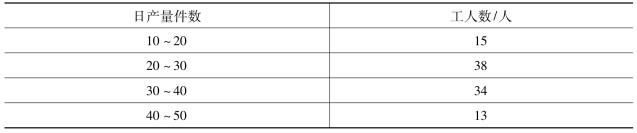
要求:

(1)计算乙组平均每个工人的日产量和标准差。

(2)比较甲、乙两生产小组哪个组的日产量差异较大。

6．对成年组和幼儿组共500人的身高资料分组，分组资料如下表所示。

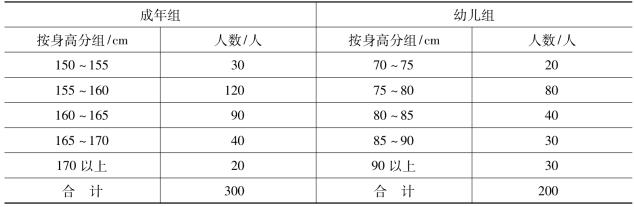
要求:

(1)分别计算成年组和幼儿组身高的平均数、标准差和离散系数。

(2)说明成年组和幼儿组平均身高的代表性哪个大?为什么?

7．某班级25名学生的统计学考试成绩数据如下:

89，95，98，95，73，86，78，67，69，82，84，89，93，91，75，86，88，82，53，80，79，81，70，87，60

试计算:

(1)该班统计学成绩的均值、中位数和四分位数。

(2)该班统计学成绩的方差、标准差。

8．有甲、乙两单位，甲单位的平均工资为950元，标准差为140元。乙单位工资资料如下表所示。

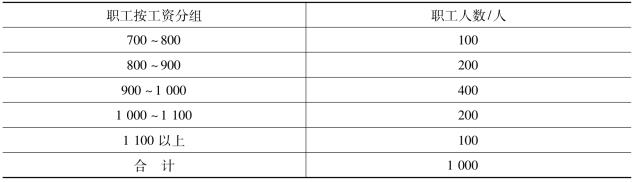
用尽可能简便的方法比较甲、乙两单位工人平均工资的代表性大小。

9．某产品资料如下表所示。

要求按以下2种方法计算产品的平均收购价格:

(1)加权算术平均数。

(2)加权调和平均数。

10．某车间生产某种产品，要经过铸造、精加工和电镀3个连续作业的工序，各工序的合格率如下表所示。试求全车间的平均合格率。