机动方式设计方法的优化

根据PWCS可观测性分析方法，这里逆向运用PWCS理论，将线性时变系统划分成多个时间段，在每个时间段内将系统近似为线性定常系统，系统是否可观测主要看可观测矩阵是否列满秩。第j（j＝1，…，n）个时间段的可观测矩阵为

［fn］为fn的反对称矩阵：

由式（6-15）知系统完全可观测取决于如下子矩阵：

首先分析Q1j，sub，由于在火箭炮射前标定的过程中只存在角运动，所以式（6-19）在进行两次角运动后可变为

其中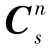，为进行第一次角运动所得的矩阵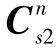；为进行第二次角运动后所得的矩阵。对式（6-21）进行初等变换如下：

因为没有线运动，所以D fs不变。(www.xing528.com)

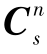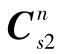通过观察Q1j，sub（2）可知，如果要使其满秩，即rank（Q1j，sub（2））＝9，　则和不能为沿同一旋转轴的单轴转动，否则rank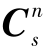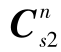（-）＝2，rank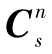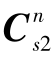（-（-）fn）≤2，最终rank（Q1j，sub（2））≤8，不满秩。

故只要同时进行两轴的角运动就可使加速度计刻度系数误差完全可观测。

接下来分析Q2j，sub：

由式（6-23）可看出，只要在3个方向上均有角速度输入，则Q2j，sub满秩。

综上，当3个方向都有角运动时惯性器件6个刻度系数误差可观测，并且长时间的单轴转动只能激励单个陀螺刻度系数误差，在设计机动方式过程中，最好将3个方向角运动同时进行，虽然对可观测性无影响，但是可以加快误差参数的收敛速度，提高标定效率。