根据PWCS可观测性分析方法，将线性时变系统划分成多个时间段，在每个时间段将系统近似为线性定常系统，系统是否可观测主要看可观测矩阵是否列满秩。第j（j＝1，…，n）个时间段的可观测性矩阵为
由式（4-36）知系统完全可观测取决于子矩阵（4-37）：
为了探求使矩阵（4-37）列满秩的条件，将其进行分块，每两列分成一块即Qj，sub＝［Q1j，subQ2j，subQ3j，sub］，只要每块都列满秩，系统就完全可观测。
对于第一块矩阵：
若载体姿态不发生变化，再经过一个时间段后：
因为rank（［fn］）＝2，rank（［fn-
］）＝2，只要fn与fn-
的矢量方向不相同Q1j，sub就能列满秩。即只要载体至少在两个方向上做变加速运动，Q1j，sub就列满秩。
若只存在姿态变化，再经过一个时间段后：
要想Q1j，sub（2）列满秩，相当于Q1j，sub（2）x＝O只存在零解。
设X＝［x1 x2］T，即
由方程（4-41）可知以下结论。
（1）若x2＝O，x1必然为O。(www.xing528.com)
（2）若x2不为O，则由（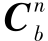
-
）x2＝O3×3知x2的矢量方向必然与载体转动轴的方向相同，由于［fn］x1＝O3×3，将式（4-41）第一个方程代入得：［fn］
x2＝O3×3，当且仅当fn的矢量方向和x2的矢量方向在n系的投影相同时，此解假设成立。在这种条件下，第一块矩阵不满秩。根据逆否命题假设，只要载体转动轴方向与比力方向不同，此矩阵就列满秩。
对于第二块矩阵：
经过一个时间段后，Q2j，sub（2）行等价为
因为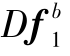
-Dfb是对角阵，要使这个可观测性子矩阵列满秩，只要
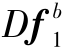-Dfb满秩，即只要经过若干个时间段载体3个轴的加速度计能分别感测到不同的输入，该矩阵即满秩。
对于第三块矩阵：
其形式与第二块矩阵相似，采用相同的分析方法可知，只要经过若干个时间段载体3个轴的陀螺仪能分别感测到不同的输入，该矩阵即满秩。
综上所述，在“速度＋姿态”匹配条件下，所设计的路径只要满足以下原则，惯导12个误差参数就完全可观测。
（1）载体在机动过程中既有角运动又有线运动且3个轴都有加速度和角速度的变化。
（2）存在某段时间载体转动轴方向与比力方向不同或载体至少在两个方向上做变加速运动。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
