基于线性时变系统可观测性判据的标定路径设计优化

考虑下面的时变系统模型：

基于线性系统理论有如下可观测性定理。

定理4-1［25］：（充分条件）设n维动态方程（4-1）的矩阵A（t）、H（t）在［t0，t1］上是n-1阶连续可微的，若存在有限时刻t*∈［t0，t1］使得

定理4-2［25］：（充要条件）设n维动态方程（4-1）的矩阵A（t）、H（t）在［t0，t1］上是解析的，则对［t0，t1］中几乎所有的t*，条件（4-2）是系统（4-1）在［t0，t1］上可观测的充要条件。

为简化标定模型、提高标定速度，本书主要选取惯导加速度计的刻度系数误差，零偏、陀螺仪的刻度系数误差和零偏为标定对象。下面推导速度加位置观测量条件下，基于线性时变系统可观测性判据的标定路径设计方法。

为便于分析，首先将状态变量分成两部分，运用设计降阶观测器的思想将系统降维处理。

令

X1＝［δVTδPT］T

X2＝［φT（Δb）T（δKa）T（εb）T（δKg）T］T

则系统（4-1）可写成

式中，Aij（t）（i，j＝1，2）是分块矩阵A（t）中与状态X1、X2对应的分块矩阵，由于X1是直接观测量，显然是可观测的，记

则式（4-3）可写为

于是讨论系统（4-3）的可观测性等价于讨论如下系统的可观测性问题：

根据系统（4-7）的特殊形式，设Ni（t）＝［Ni1（t）Ni2（t）Ni3（t）］，i＝0，1，…，n-1，其中Ni1（t）是3×3方阵，Ni2（t）和Ni3（t）是3×6方阵，记，则

所以矩阵F（t）可以写成如下分块矩阵：

其中

矩阵F（t）列满秩的必要条件是F1（t）、F2（t）和F3（t）都列满秩。下面分别分析各子矩阵列满秩的条件。

首先讨论F1（t）列满秩的条件：

根据式（4-8）有。

F1（t）列满秩的充要条件是如下系统可观测：(www.xing528.com)

根据Aφφ和AVφ的具体形式可得

因此可近似认为

关于矩阵F1（t）列满秩有以下定理成立。

定理4-3：当fU（t*）≠0并且下列条件之一成立时F1（t）列满秩。

证明　当fU（t*）≠0时AVφ行等价于矩阵

所以

其中“≅”代表矩阵等价。如果条件（1）成立，则上面矩阵第1、2、3行组成的子矩阵列满秩，如果条件（2）成立，则上面矩阵第1、2、4行组成的子矩阵列满秩，如果条件（3）成立，则上面矩阵第1、2、5行组成的子矩阵列满秩，因此，只要条件（1）（2）（3）之一成立，则F1（t）列满秩。

其次讨论F2（t）列满秩的条件，有如下定理成立。

定理4-4：矩阵F2（t）列满秩的充要条件是不同时为0，其中ai（t*）是i加速度计感受的加速度（i＝x，y，z）。

证明　由式（4-8）可知Ni2（t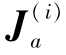）＝，i＝0，…，n-1，又由于Ja（t）＝［］所以：

则

对式（4-17）进行初等行变换得

最后讨论F3（t）列满秩的条件，矩阵F3（t）是待估参数［（εb）T（δKg）T］与系统观测量（t）之间的转换系数。因此F3（t）的列满秩性反映了参数［（εb）T（δKg）T］的可估计性，对于参数［（εb）T（δKg）T］的可估计性有如下定理成立。

定理4-5：与陀螺相关的参数［（εb）T（δKg）T］可估计的必要条件是

综上所述，要使在速度加位置匹配条件下，惯导12个误差参数完全可观测，标定路径设计原则如下［20］。

（1）存在时间t*使下列条件之一成立。

（2）存在时间t*使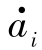（t*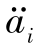），（t*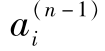），…，（t*）不同时为零（i＝x，y，z）。

（3）存在时间t*使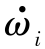（t*）≠0，i＝x，y，z。

以上设计原则只是系统完全可观测的必要条件，在设计好标定路径后，还得验证其可观测性矩阵是否满秩，若不满秩，还得进行调整，直到可观测性矩阵满秩为止。