三种匹配模式误差参数标定分析

为了进一步验证三种匹配模式下弹载惯导在线标定的效果，利用MATLAB软件平台分别对三种匹配模式下在线标定过程进行仿真试验，采用标准卡尔曼滤波算法对各误差参数进行估计，惯性器件各误差参数的滤波估计结果如图3-6、图3-7所示（其中直线表示预先设定值，曲线表示滤波估计值）。

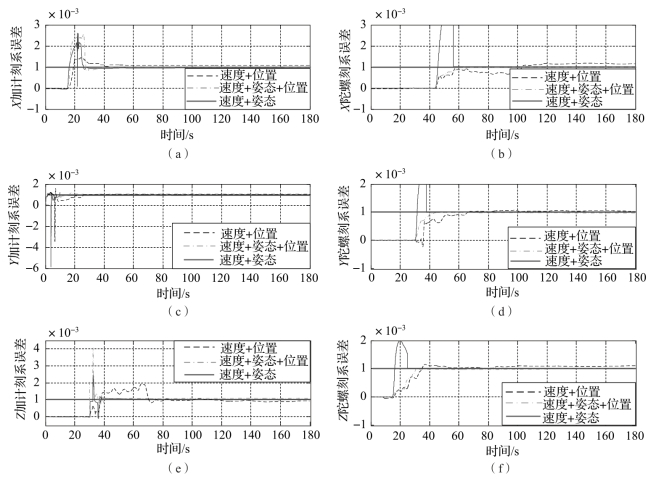
图3-6　加速度计和陀螺刻度系数误差估计曲线

（a）X加计刻系误差；（b）X陀螺刻系误差；（c）Y加计刻系误差；
（d）Y陀螺刻系误差；（e）Z加计刻系误差；（f）Z陀螺刻系误差

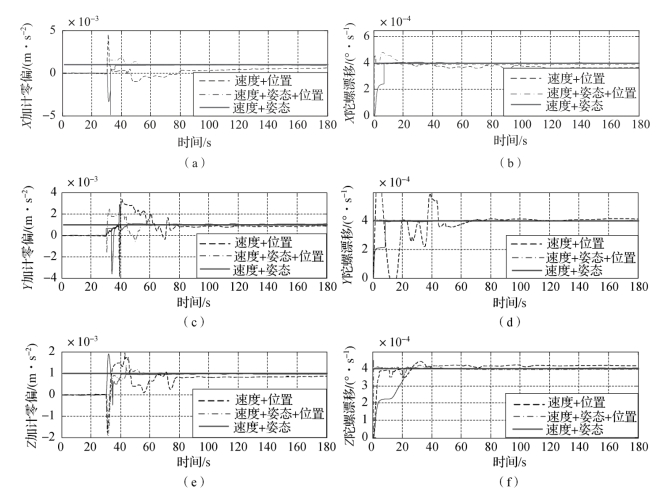
图3-7　加速度计零偏和陀螺漂移估计曲线

（a）X加计零偏；（b）X陀螺漂移；（c）Y加计零偏；
（d）Y陀螺漂移；（e）Z加计零偏；（f）Z陀螺漂移

由图3-6、图3-7可以看出，采用“速度＋姿态”匹配模式时，惯性器件12个误差参数的标定效果都比较好，且除Z轴加速度计零偏之外的11个误差参数的收敛速度都比较快；采用“速度＋姿态＋位置”匹配模式时，惯性器件12个误差参数的标定效果与采用“速度＋姿态”匹配时相当，但部分误差参数的收敛时间有所增长，尤其是Z轴加速度计零偏和Z轴陀螺漂移的收敛时间增长明显；当采用“速度＋位置”匹配时各误差参数的收敛效果一般，特别是X轴、Y轴加速度计零偏以及X轴陀螺刻度系数误差3个参数收敛精度较差。

由图3-6、图3-7得到的标定结果与表3-4所示三种匹配模式下12个误差参数的可观测指标是相符的，证明了新的可观测度分析方法是可靠的。(www.xing528.com)

为进一步考察不同观测量对标定效果的影响，下面分别从标定精度和收敛时间两方面对标定结果进行量化分析。当滤波基本达到稳定后，对140～180 s时间段内的滤波估计值求平均值，用得到的结果代表单次仿真的滤波估计值，且为了降低每次试验中随机噪声对滤波估计的影响，将仿真试验重复5次，对5次仿真估计值再求平均值作为最终的误差估计值并求出误差标定的相对精度（相对精度＝｜估计值-预设值｜÷预设值），结果如表3-5所示。同时，将不同匹配模式下各误差参数的收敛时间（各误差参数受到相应机动方式激励后估计曲线从开始收敛到曲线达到稳态所用的时间）总结如表3-6所示。

表3-5　不同匹配模式下各误差参数标定相对精度　单位：%

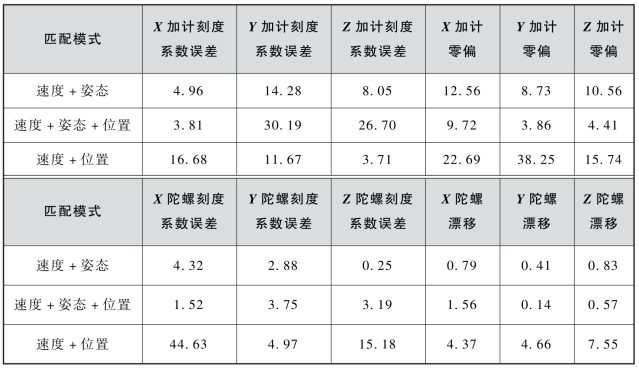
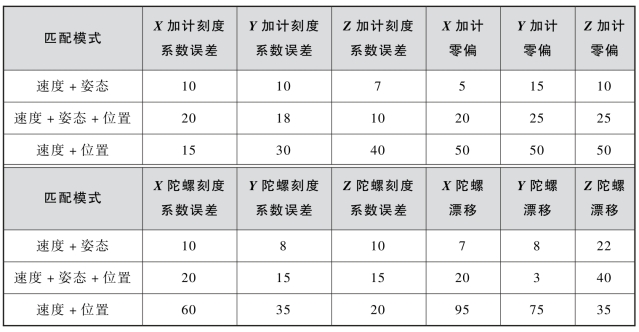
表3-6　不同匹配模式下各误差参数收敛时间　单位：s

由表3-5可以看出，对比“速度＋姿态”匹配模式下各误差参数的标定精度，采用“速度＋姿态＋位置”匹配时，Y轴、Z轴加速度计刻度系数误差，Y轴、Z轴陀螺刻度系数误差和X轴陀螺漂移等5个误差参数的标定精度有一定下降，而X轴加速度计刻度系数误差、三轴加速度计零偏、X轴陀螺刻度系数误差及Y轴、Z轴陀螺漂移等7个误差参数的标定精度都有提高；采用“速度＋位置”匹配模式相对于“速度＋姿态”匹配模式，Y轴、Z轴加速度计刻度系数误差的标定精度有一定提高，其余10个误差参数的标定精度都明显降低，其中X轴、Y轴加速度计零偏及X轴陀螺刻度系数误差的标定精度下降较明显。

从表3-6可以看出，在“速度＋姿态”匹配模式基础上增加“位置”观测量后各误差参数的收敛时间普遍增长，尤其是X轴、Z轴加速度计零偏以及X轴陀螺漂移的收敛时间增长明显；而“速度＋位置”匹配相比于“速度＋姿态”匹配，除了X轴加速度计刻度系数误差和Z轴陀螺刻度系数误差之外，其余误差参数的标定时间都大幅增长。

综上所述，在“速度＋姿态”匹配模式基础上增加“位置”观测量后，7个误差参数的估计精度都有一定的提高，但有11个误差参数的收敛时间变长；采用“速度＋位置”匹配时，除Y轴、Z轴加速度计刻度系数误差之外，其余各误差参数的标定效果都比较差。因此，在选择匹配模式时要根据实际情况对标定效率及标定精度做合理取舍。本书研究的误差标定是以弹载捷联惯导系统为应用背景，结合火箭炮工作实际，综合考虑标定精度及标定效率，选取“速度＋姿态”匹配为最优匹配模式。