验证可观测度计算方法的特点及准确性的仿真试验

为了验证3.3.2小节给出的可观测度计算方法的特点及准确性，分别采用所提出的可观测度分析方法和基于SVD的方法对系统进行可观测度分析。

1.滤波模型

依据弹载捷联惯导系统误差方程，构建滤波模型如下：

其中，W、V为不相关的高斯白噪声，X＝［δVnΦnμbδkaδkgεb］T，Z＝［δVnΦn］T；δVn为系统三轴向速度误差；Φn为系统三轴向姿态误差；μb为子惯导相对主惯导的安装误差角；δka、δkg分别为加速度计和陀螺三轴向刻度系数误差；∇b、εb分别为加速度计和陀螺三轴向零偏。

由系统的速度、位置、姿态误差方程可得系统状态矩阵：

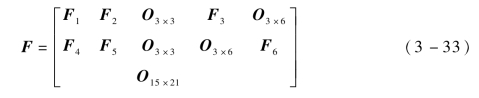
其中

观测矩阵为

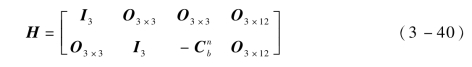
式（3-32）～式（3-40）中，为导航系到载体系的变换矩阵；Ve、Vn、Vu分别为载体三轴向速度；L为运载体所处纬度；Rm、Rn分别为地球子午圈和卯酉圈半径；ωie为地球自转角速度。

2.仿真条件设置

参照文献［57］，在轨迹发生器中设定理想状态下炮车的机动路径如下。

（1）炮车由静止开始做变加速直线运动10 s后保持匀速直线行驶5 s。

（2）炮车做匀速转弯机动10 s后保持匀速直线行驶5 s。

（3）炮车通过一拱桥，10 s后继续匀速直线行驶。

为了满足卡尔曼滤波要求，对式（3-32）进行离散化，且系统各初始参数设置如下。

设初始纬度为30°，经度为118°，状态量X初值为0，陀螺仪及加速度计初始误差参数设置如表3-1所示。

表3-1　陀螺仪及加速度计初始误差参数设置

初始方差阵为(www.xing528.com)

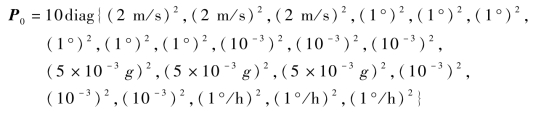
系统噪声协方差阵为

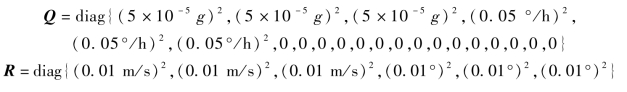
3.可观测度分析结果

1）基于最小二乘估计的可观测度分析方法计算结果

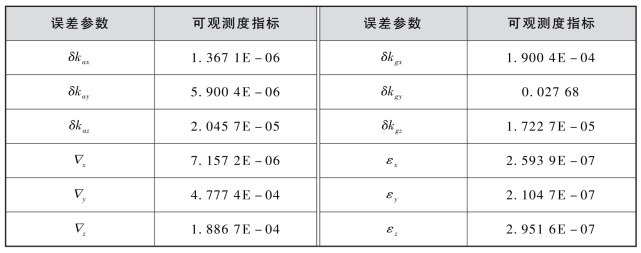
采用3.3.2小节介绍的可观测度分析方法计算各误差参数的可观测度，结果如表3-2所示（为了简化表示方法，计算时用E表示以10为底数的幂，例如：2.0E-05表示2.0×10-5）。

表3-2　新的可观测度分析方法计算结果

2）基于SVD的可观测度分析方法计算结果

为了证明表3-2中计算结果的正确性，本小节利用当前在工程实际中应用较为成熟的基于SVD分解的可观测度分析方法对系统各误差参数的可观测度进行计算，结果如图3-3、表3-3所示。图3-3中每幅小图表示一个状态变量对应的奇异值，图3-3（a）至图3-3（l）依次表示状态量δkax、δkay、δkaz、∇x、∇y、∇z、δkgx、δkgy、δkgz、εx、εy、εz的奇异值。

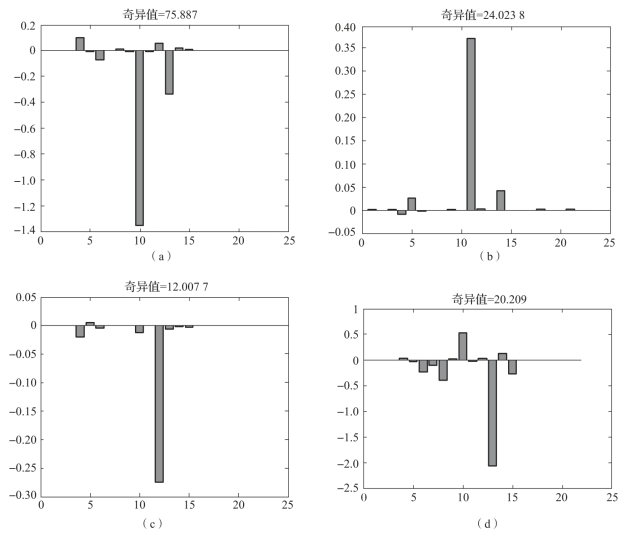
图3-3　各误差参数奇异值

（a）状态量δkax的奇异值；（b）状态量δkay的奇异值；
（c）状态量δkaz的奇异值；（d）状态量∇x的奇异值

由表3-2中的计算结果可以看出，除Y轴陀螺刻度系数误差δkgy之外，其余11个误差参数的可观测度指标都比较小，根据3.3.2小节给出的可观测度定义可知，Y轴陀螺刻度系数误差的可观测度较差，其余11个误差参数的可观测度比较强。由表3-3可以看出，除Y轴陀螺刻度系数误差的奇异值非常小之外，其余11个误差参数的奇异值都大于0.9，说明Y轴陀螺刻度系数误差的可观测性较差，其余11个误差参数的可观测性都很好。由图3-3可以看出，虽然基于SVD的方法定义每幅分图都代表一个误差参数的奇异值，且定义奇异值的大小即代表该误差参数的可观测度，但实际上每幅图中的奇异值是几个参数互相耦合的奇异值结果。

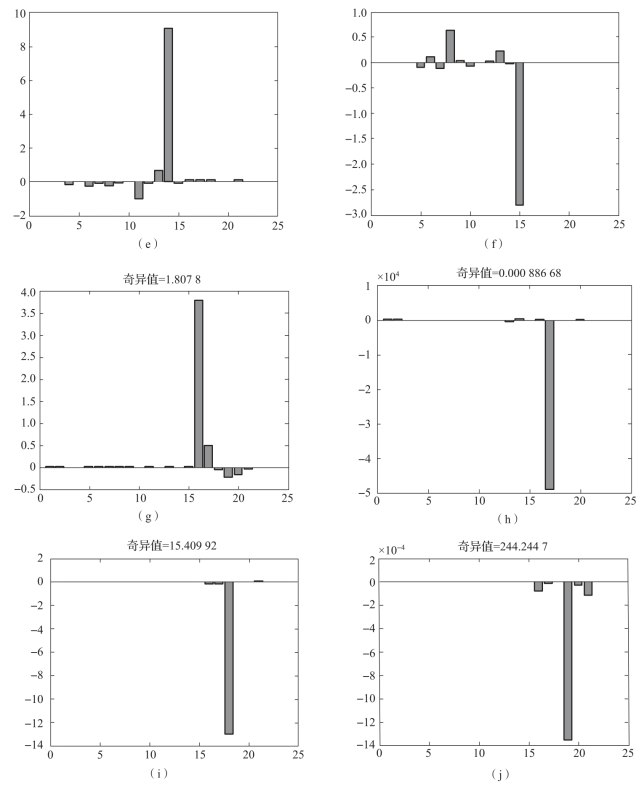
图3-3　各误差参数奇异值（续）

（e）状态量∇y的奇异值；（f）状态量∇z的奇异值；
（g）状态量δkgx的奇异值；（h）状态量δkgy的奇异值；
（i）状态量δkgz的奇异值；（j）状态量εx的奇异值

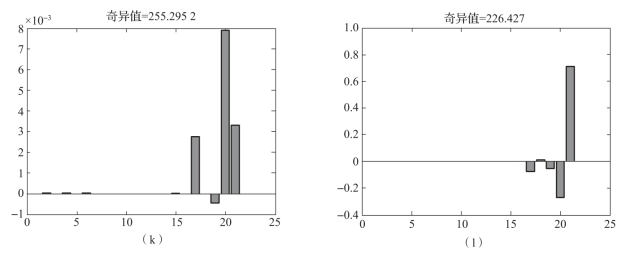
图3-3　各误差参数奇异值（续）

（k）状态量εy的奇异值；（l）状态量εz的奇异值

表3-3　基于SVD的可观测度分析方法计算结果

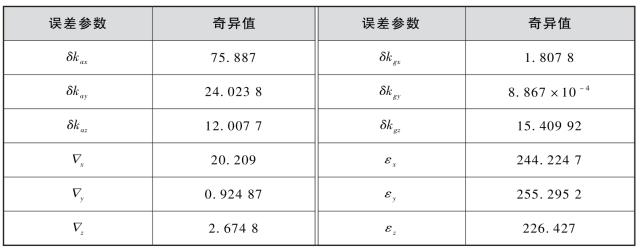
采用基于SVD方法得出的结果与采用3.3.2小节提出的可观测度分析方法的计算结果是一致的。但是，由SVD方法的计算流程可知，采用SVD方法计算系统可观测度时，需要求出每一时刻的Q、Qs、σ以及X（0），而基于最小二乘估计的可观测度分析方法只需求出每一时刻的Fk，0即可，因此相对于新的可观测度分析方法而言，SVD方法计算量大、效率低，且得到的可观测度是几个误差参数相互耦合的结果，并不是某个独立参数的可观测度。