基于最小二乘估计的可观测度分析方法

系统在一定的时间内通过观测量确定状态量的能力称为系统的可观测性，误差参数的估计精度与系统的可观测性密切相关［66］。考虑到当前常用的可观测性分析方法都存在一定不足，本小节从初始状态的最小二乘估计角度，对各状态量进行可观测度分析，考虑如下离散线性系统：

其中，xi∈Rn为ti时刻系统的状态量；Fi，i-1∈Rn×n为ti-1至ti时刻系统的状态转移矩阵；zi∈Rm为系统的观测值；Hi为系统的观测矩阵；vi为系统的观测噪声，且满足E［vi］＝0，E［vi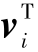］＝Ri；定义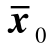、P0分别为初始状态x0的均值和方差。

设系统在tk时刻得到的观测值为　｛z1，z2，…，zk｝，定义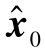为 式（3-20）中初始状态x0的最小二乘估计，由最小二乘估计的定义可得

式中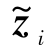，＝zi-Hixi＝zi-HiFi，0x0。

将式（3-21）两端对x0求偏导可得

令式（3-22）等号左端为零，则能够计算得出x0的最小二乘估计为

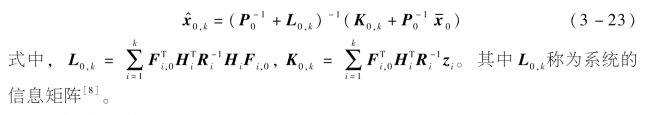
设估计误差为

将式（3-23）代入式（3-24）可得

将zi＝HiFi，0x0＋vi代入式（3-25）得

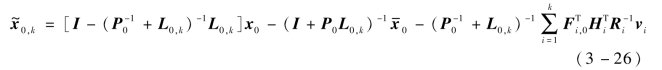
可以证明I-（＋L0，k）-1L0，k与（I＋P0L0，k）-1是相等的。　具体证明如下：(www.xing528.com)

设D、E为两个可逆方阵，B、C为两个维数适当的矩阵，由矩阵求逆定理可得

所以

则式（3-26）可以写成

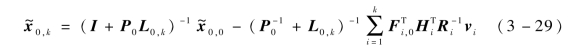
式（3-29）等号右侧第一项表示估计误差的衰减程度，第二项表示观测噪声对估计误差的影响，在此忽略观测噪声的影响，则式（3-29）可简化为

由式（3-30）可得，矩阵（I＋P0L0，k）-1的对角线元素表示各误差参数相对于其初始估计误差的变化量。变化量越大，说明该误差参数越容易被观测，因此定义（I＋P0L0，k）-1中的对角线元素为对应的系统各状态量的可观测度指标，即

由上述可观测度定义可知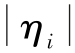：越靠近0，说明估计误差的衰减越明显，则对应状态量的可观测度越大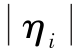；越靠近1，说明估计误差的衰减越小，对应状态量的可观测度就越小。

根据以上可观测度算法可以看出，I、P0都是已知的，要求可观测度指标，关键是要求出L0，k，而L0，k＝，其迭代流程如图3-2所示，其中设。

图3-2　可观测度算法流程

通过图3-2所示的算法迭代流程可以看出，相对于常用可观测度分析方法，此方法有以下优点。

（1）计算量小，效率高。采用该算法每一时刻只需要计算出Mk就能求得相应时刻的可观测度指标，且Mk中的Hk、Rk都是已知的，只需求出Fk，0即可。

（2）计算结果含义明确。矩阵（I＋P0L0，k）-1的对角线元素中每一个数值代表着对应状态量的可观测度，不存在互相之间的耦合。