卡尔曼滤波基本理论简介

卡尔曼滤波算法是在1960年由Kalman首次提出的一种递推最优估计理论。由于采用了状态空间法描述系统，且算法是递推形式，因此卡尔曼滤波能够处理多维和非平稳的随机过程。系统状态方程、观测方程和系统噪声统计特性是卡尔曼滤波估计过程中的三个必要条件。

考虑如下离散系统模型：

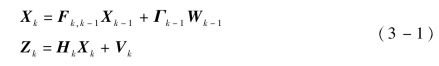
式中，Xk为tk时刻系统的状态变量；Fk，k-1为tk-1时刻至tk时刻系统的一步状态转移矩阵；Xk-1为tk-1时刻系统的状态变量；Γk-1为tk-1时刻系统噪声驱动矩阵；Wk-1为tk-1时刻系统状态噪声矩阵；Zk为tk时刻系统的观测变量；Hk为tk时刻观测矩阵；Vk为tk时刻观测噪声矩阵。假定系统噪声序列协方差阵Qk为非负定阵，观测噪声序列协方差阵Rk为正定阵，则Xk的估计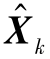按照下述方程求解［65］。

状态一步预测方程如下：

状态估计方程如下：

滤波增益方程如下：

(www.xing528.com)

一步预测均方误差方程如下：

估计均方误差方程如下：

式（3-2）～式（3-6）即为卡尔曼滤波算法的5个基本递推方程。只要已知初值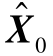和P0，则依据k时刻系统的观测值Zk，就能够通过递推方程求得k时刻的状态估计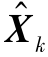（k＝1，2…）。

图3-1为卡尔曼滤波算法递推过程。如图3-1所示，卡尔曼滤波由两个计算回路组成：独立的增益计算回路和依赖于增益计算回路的滤波计算回路。从递推过程中使用信息的先后顺序看，卡尔曼滤波在一个完整的滤波周期内又具有时间更新和量测更新两个明显的信息更新过程。

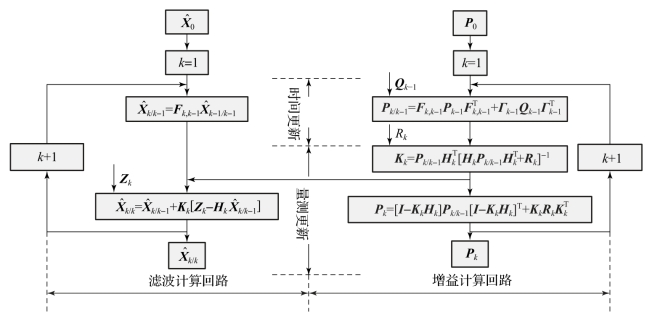
图3-1　卡尔曼滤波算法递推过程

卡尔曼滤波最大的优势就是当建立的模型符合卡尔曼滤波器的条件时，仅利用k-1时刻的估计值和k时刻的观测值即可实时估计出系统状态。正是由于这一特点，卡尔曼滤波理论一经提出立即受到工程应用的重视，其作为一种重要的最优估计理论已经在多个研究领域被广泛应用。